tR
» » Bài 2 Tìm kiếm nhị phân

Trắc nghiệm
Bài 2 Tìm kiếm nhị phân

Câu 1: Lấy phần tử đứng giữa dãy để so sánh với x, nếu phần tử đó chính là x thì kết luận gì?

  •  Chưa tìm thấy x và tiếp tục thuật toán.
  •  Chưa tìm thấy x và kết thúc thuật toán.
  •  Đã tìm thấy x và kết thúc thuật toán.
  •  Đã tìm thấy x và tiếp tục thuật toán.

Câu 2: Trong bài toán tìm kiếm nhị phân, đối với dãy đã sắp xếp tăng dần khi nào phạm vi tìm kiếm nằm ở nửa sau của dãy:

  • Khi số cần tìm lớn hơn phần tử giữa của phạm vi tìm kiếm.
  • Khi số cần tìm nhỏ hơn phần tử giữa của phạm vi tìm kiếm.
  • Khi số cần tìm lớn hơn phần tử đầu tiên của dãy.
  • Khi số cần tìm nhỏ hơn phần tử cuối cùng của dãy.

Câu 3: Trong các phát biểu sau, phát biểu nào sai?

  • Tìm kiếm nhị phân chia dãy làm hai nửa dài xấp xỉ bằng nhau và chỉ cần tìm kiếm trong một nửa dãy.
  • Tìm kiếm nhị phân chia dãy làm hai nửa dài đúng bằng nhau và chỉ cần tìm kiếm trong một nửa dãy.
  • Tìm kiếm nhị phân lặp lại việc chia đôi dãy cho đến khi dãy chỉ còn một phần tử.
  • Tìm kiếm nhị phân nhanh hơn tìm kiếm tuần tự.

Câu 4: Bài toán nào sau đây áp dụng được thuật toán tìm kiếm nhị phân:

  • Cho dãy 1, 3, 5, 6. Tìm vị trí của số 5 trong dãy.
  • Cho dãy 1, 5, 3, 6. Tìm vị trí của số 5 trong dãy.
  • Cho dãy 6, 5, 4, 3, 2, 1. Hãy tìm xem số 3 có trong dãy này không.
  • Cả A và C.

Câu 5: Ý nghĩa của việc chia một bài toán thành những bài toán nhỏ hơn?

  •  Dễ thực hiện và nhanh cho ra kết quả.
  •  Cho kết quả chính xác hơn.
  •  Cho kết quả cụ thể hơn.
  •  Cho kết quả khái quát hơn.

Câu 6: Thuật toán tìm kiếm nhị phân cần bao nhiêu bước để tìm thấy Thailand trong danh sách tên các nước sau:
Brunei, Campodia, Laos, Myanmar, Singpore, Thailand, Vietnam<
  • 1
  • 2 
  • 3
  • 4

Câu 7: Trong các câu sau, câu nào đúng?

  • Tìm kiếm nhị phân chỉ áp dụng được cho dãy đã sắp xếp thứ tự tăng dần.
  • Tìm kiếm nhị phân chỉ áp dụng được cho dãy đã sắp xếp thứ tự giảm dần.
  • Tìm kiếm nhị phân chỉ áp dụng được cho dãy đã sắp thứ tự.
  • Tìm kiếm nhị phân áp dụng được cho dãy bất kì.

Câu 8: Cho dãy số 0, 1, 2, 4, 6, 8, 9. Bài toán “Tìm vị trí của số 8 trong dãy” có phần tử giữa là:

  • 4
  • 2
  • 6
  • 8

Câu 9: Trong bài toán tìm kiếm nhị phân, đối với dãy đã sắp xếp tăng dần khi nào phạm vi tìm kiếm nằm ở nửa đầu của dãy:

  • Khi số cần tìm lớn hơn phần tử giữa của phạm vi tìm kiếm.
  • Khi số cần tìm nhỏ hơn phần tử giữa của phạm vi tìm kiếm.
  • Khi số cần tìm lớn hơn phần tử đầu tiên của dãy.
  • Khi số cần tìm nhỏ hơn phần tử cuối cùng của dãy.

Câu 10: Khi bắt đầu thuật toán, phạm vi tìm kiếm là gì?

  •  Dãy đã được tìm kiếm.
  •  Dãy đã cho ban đầu đã được sắp xếp.
  •  Dãy đã cho ban đầu chưa được sắp xếp.
  •  Dãy số bình thường.

Câu 11: Điều kiện lặp của thuật toán tìm kiếm nhị phân là gì?

  • Chưa tìm thấy phần tử cần tìm.
  • Chưa hết danh sách.
  • Chưa tìm thấy phần tử cần tìm hoặc chưa hết danh sách.
  • Chưa tìm thấy phần tử cần tìm và chưa hết danh sách.

Câu 12: Nhận định nào sau đây đúng nhất về thuật toán tìm kiếm nhị phân?

  •  Chỉ áp dụng tìm kiếm nhị phân với dãy số tăng dần.
  •  Có thể áp dụng tìm kiếm nhị phân với bất kì dãy số nào.
  •  Không phải với bất cứ dãy số nào cũng có thể áp dụng được thuật toán tìm kiếm nhị phân. Vì tìm kiếm nhị phân chỉ áp dụng với dãy số đã được sắp xếp tăng dần hoặc giảm dần.
  •  Chỉ áp dụng tìm kiếm nhị phân với dãy số giảm dần.

Câu 13: Điều kiện lặp trong bài toán tìm kiếm nhị phân là:

  • Kết quả tìm thấy.
  • Phạm vi tìm kiếm dài hơn 1 và kết quả chưa tìm thấy.
  • Xét hết dãy số.
  • Cả A và C đều đúng.

Câu 14: Cho dãy số 0, 1, 2, 4, 6, 8, 9. Bài toán “Tìm số x = 4 trong dãy” có số lần lặp là:

  • 0
  • 1
  • 2
  • 3

Câu 15: Biết rằng dãy số đã sắp thứ tự. Có thể áp dụng tìm kiếm nhị phân cho bài toán nào?

  • Tìm tất cả các số bằng x có trong dãy.
  • Tìm số đầu tiên bằng x.
  • Tìm số cuối cùng bằng x.
  • Tìm số bằng x trong dãy.

Câu 16: Phát biểu đúng nhất về “Thuật toán tìm kiếm nhị phân” (tìm x trong dãy số đã được sắp thứ tự không giảm)?

  •  Là thuật toán tìm kiếm x trong dãy đã sắp xếp thứ tự với ý tưởng chia đôi để giảm nhanh phạm vi tìm kiếm.
  •  Là thuật toán tìm kiếm x trong dãy đã sắp xếp thứ tự với ý tưởng chia ba phần để giảm nhanh phạm vi tìm kiếm.
  •  Là thuật toán tìm kiếm x trong dãy với ý tưởng chia đôi để giảm nhanh phạm vi tìm kiếm.
  •  Là thuật toán tìm kiếm x trong dãy đã sắp xếp thứ tự với ý tưởng chia đôi để tăng nhanh phạm vi tìm kiếm.

Câu 17: Cho dãy số 2, 4, 6, 8, 9. Bài toán “Tìm vị trí của số 8 trong dãy”, có phạm vi tìm kiếm là:

  • Nửa dãy đầu.
  • Nửa dãy sau.
  • Tất cả dãy.
  • Không có phạm vi.

Câu 18: Thuật toán tìm kiếm x trong dãy đã sắp xếp thứ tự với ý tưởng chia đôi dần để giảm nhanh phạm vi tìm kiếm được gọi là gì?

  •  Thuật toán tìm kiếm nhị phân.
  •  Thuật toán tìm kiếm tuần tự.
  •  Thuật toán liệt kê.
  •  Các đáp án trên đều sai.

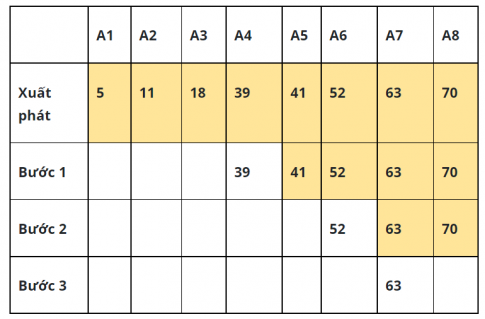
Câu 19: Cho dãy số 5, 11, 18, 39, 41, 52, 63, 70. Hãy sắp xếp diễn biến từng bước tìm kiếm nhị phần để tìm kiếm x = 60 trong dãy trên.
Tìm x = 60:
Cho dãy số 5, 11, 18, 39, 41, 52, 63, 70. Hãy sắp xếp diễn biến từng bước tìm kiếm nhị phần để tìm kiếm x = 60 trong dãy trên.
1. Kết thúc thuật toán: Không tìm thấy x có trong dãy.
2. Phạm vi tìm kiếm từ A7 đến A8. Lấy A7 có vị trị giữa dãy. Vì x < a7 nên nửa sau dãy chắc chắn không chứa x = 60, tiếp theo chỉ cần tìm trong nửa dãy. Như vậy, phạm vi tìm kiếm tiếp theo là dãy con một phần tử a7.
3. Phạm vi tìm kiếm từ dãy A5 đến A8. Lấy A6 có vị trí giữa dãy. Vì x > A6 nên nửa đầu dãy chắc chắn không chứa x = 60. Tiếp theo chỉ cần tìm trong nửa sau của dãy. Phạm vi tìm kiếm từ A7 đến A8.
4. Phạm vi tìm kiếm từ dãy A1 đến A8. Lấy A4 là số có vị trí giữa dãy. Vì x > A4 nên nửa đầu dãy chắc chắn không chứa x = 60. Tiếp theo chỉ cần tìm trong nửa sau của dãy. Phạm vi tìm kiếm từ A5 đến A8.

  •  2 – 1 – 3 – 4.
  •  1 – 2 – 3 – 4.
  •  4 – 3 – 2 – 1.
  •  3 – 2 – 1 – 4.

Câu 20: Để tìm một số trong dãy đã được sắp xếp tăng dần, thuật toán tìm kiếm nhanh nhất là:

  • Tìm kiếm tuần tự.
  • Tìm kiếm nhị phân.
  • Cả A và B.
  • Không có thuật toán nào.

Câu 21: Thuật toán tìm kiếm nhị phân cần thực hiện bao nhiêu bước để thông báo không tìm thấy số 10 trong danh sách [2, 5, 8, 11, 14, 17] ?

  •  2                        
  •  3                        
  •  4                        
  •  5

Câu 22: Thực hiện thuật toán tìm kiếm nhị phân để tìm số 10 trong danh sách [2, 4 ,6, 8, 10, 12]. Đầu ra của thuật toán là?

  • Thông báo “Không tìm thấy”.
  • Thông báo “Tìm thấy”.
  • Thông báo “Tìm thấy”, giá trị cần tìm tại vị trí thứ 5 của danh sách.
  • Thông báo “Tìm thấy”, giá trị cần tìm tại vị trí thứ 6 của danh sách.

Hãy trả lời các câu hỏi để biết kết quả của bạn


tháng 1 05, 2024

0 Comments:

Đăng nhận xét

Đăng ký: Đăng Nhận xét (Atom)
 
Top