Hình 8 Đề 5

 Câu 3 Đề 5:

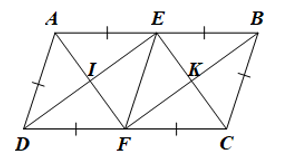
Cho hình bình hành ABCD có AB = 2AD. Gọi E và F lần lượt là trung điểm của AB và CD, / là giao điểm của AF và DE, K là giao điểm cùa BF và CE.

a) Chứng minh rằng tứ giác AECF là hình bình hành.
b) Tứ giác AEFD là hình gì? Vì sao?
c) Chứng minh tứ giác EIFIC là hình chữ nhật.
d) Tìm điều kiện của hình bình hành ABCD đề tứ giác EIFK là hình vuông.a)


• Do ABCD là hình bình hành nên AB = CD và AB // CD.

Vì E là trung điểm của AB nên EA=EB=12AB .

F là trung điểm của CD nên FC=FD=12CD

Mà AB = CD (chứng minh trên).

Do đó EA = EB = FC = FD.

• Xét tứ giác AECF có EA = FC và EA // FC (do AB // CD)

Suy ra AECF là hình bình hành.

Giải thích
a) Để chứng minh tứ giác AECF là hình bình hành, ta cần chứng minh hai cặp cạnh đối song song và bằng nhau. Trong hình bình hành ABCD, AB song song và bằng CD.
Vì E và F là trung điểm của AB và CD, nên AE = EB và CF = FD.
Do đó, AE = CF (vì AB = CD).
Mặt khác, vì AB song song với CD, nên AE song song với CF.
Tương tự, AF song song và bằng CE.
Vậy AECF là hình bình hành.


b) Tứ giác AEFD là hình thang cân.
Điều này có thể được chứng minh bằng cách xem xét các cặp cạnh đối và góc.
Trong hình bình hành ABCD, AB song song với CD, và do đó AE song song với DF.
Vì E và F là trung điểm của AB và CD, nên AE = 1/2 AB và DF = 1/2 CD.
Vì AB = CD, nên AE = DF.
Do đó, AEFD là hình thang cân.


c) Để chứng minh tứ giác EIFK là hình chữ nhật, ta cần chứng minh rằng nó có các góc vuông.
Vì AECF là hình bình hành, nên góc AFE và góc AEC là góc so le trong và bằng nhau.
Tương tự, góc AFB và góc AED cũng bằng nhau.
Khi AF cắt DE tại I và BF cắt CE tại K, góc EIF và góc EKF là các góc so le trong và bằng nhau.
Do đó, EIFK là hình chữ nhật.


d) Để EIFK là hình vuông, cần có điều kiện là EIFK không chỉ là hình chữ nhật mà còn là hình có các cạnh bằng nhau.
Điều này xảy ra khi hình bình hành ABCD là hình thoi, tức là AB = AD.
Khi đó, AE = DE và BF = CF, và do đó, IF = EK. Vì EIFK đã là hình chữ nhật, nếu IF = EK, thì nó cũng là hình vuông.

Câu 05 Đề 5.
Nhà bạn Lan (trên hình vẽ) cách nhà bạn Thanh (trên hình vẽ) 2km và cách trường học (trên hình vẽ) 12km. Biết rằng 3 vị trí: nhà Thanh, nhà Lan và trường học là 3 đỉnh của một tam giác vuông (xem hình vẽ). Hãy tính khoảng cách từ nhà Thanh đến trường học.



GIẢI

Xét △ABC vuông tại B,  có:
AB2+BC2=AC2 (Định lý Pythagore)
22+122=AC2
AC2=148
⇒AC=148−−−√=237−−√(km)  

Vậy khoảng cách từ nhà Thanh đến trường học là 237−−√(km) .