Hình 8 Đề 16

Bài 3
Một người chạy trên con dốc có độ dài AC = 10m.
Biết đỉnh dốc có độ cao CB = 4m.
Tính khoảng cách từ A đến B ( làm tròn đến hàng đơn vị)?

Trong tam giác ABC có: góc B = 90 độ
=> Tam giác ABC vuông tại B
Áp dụng định lí Py-ta-go ta có:
$AC^2 = BC^2 + AB^2$
    => $AB^2 = AC^2 - BC^2$
    = $10^2 - 4^2$
    = 100 - 16 = 84
    => AB ≈ 9 (9,165151...)
Vậy khoảng cách từ A đến B là khoảng 9m

Bài 4
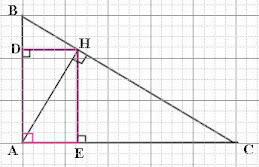
Cho tam giác ABC vuông tại A (AB <AC) có đường cao AH. Kẻ HD vuông góc với AB (D thuộc AB) và HE vuông góc với AC (E thuộc AC).
a) Chứng minh tứ giác ADHE là hình chữ nhật. 

b) Gọi F là điểm đối xứng với điểm B qua H và K là điểm đối xứng với điểm A qua H. Chứng minh AF vuông góc với CK

GIẢI

a) Chứng minh tứ giác ADHE là hình chữ nhật.

Xét tứ giác ADHE, ta có:

 $\widehat{A}$=$\widehat{D}$=$\widehat{E}$=$90^0$

Tứ giác này có 3 góc vuông, là hình chữ nhật.

b) Chứng minh AF vuông góc với C

Xét tam giác ABK, ta có:

$BH \perp{AK}$ (gt)

HA = HK (gt)

$\Rightarrow$ BA = BK ( t/c trung trực)

$\Rightarrow$ tam giác ABK cân tại B

$\Rightarrow$$\widehat{A_1} = \Rightarrow{K_1}$

Xét tam giác ACK, ta có:

HA = HK (gt)

$HC \perp{AK}$ (gt)

$\Rightarrow$ CA = CK ( t/c trung trực)

$\Rightarrow$ tam giác ACK cân tại C

$\Rightarrow$$\widehat{A_2} = \Rightarrow{K_2}$

Xét tứ giác AFBK, ta có:

 Hai đường chéo AK và BF cắt nhau tại trung điểm mỗi đường, là hình bình hành.

$\Rightarrow$ BK // AF hay BK // AI.

Mà $\widehat{A_1} + \Rightarrow{A_2}$ = $90^0$

$\Rightarrow$ $\widehat{K_1} + \Rightarrow{K_2}$ = $90^0$

Xét tứ giác AIKB, ta có:

BK // AI  

mà $BK \perp{KC}$ 

nên AI cũng $\perp{KC}$ tại I (t/c hai đường //)