Hình 8 Đề 15

ĐỀ 15
Bài 3 Đề 15

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Kẻ MD vuông góc với AB tại D.
a) Chứng minh: Tứ giác ADMC là hình thang vuông.
b) Vẽ E đối xứng M qua D. Chứng minh tứ giác ACME là hinh bình hành.

GIẢI


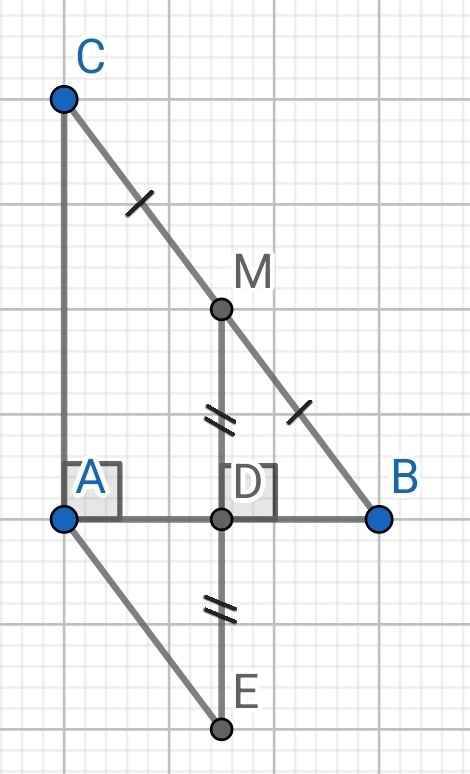
a) Do ∆ABC vuông tại A (gt)
    ⇒ AB ⊥ AC
Mà MD ⊥ AB (gt)
    ⇒ AC // MD
    ⇒ ADMC là hình thang

Mà ∠CAD = 90⁰ (∆ABC vuông tại A)
    ⇒ ADMC là hình thang vuông

b) ∆ABC có:
M là trung điểm của BC (gt)
MD // AC (cmt)
    ⇒ D là trung điểm của AB
    ⇒ MD là đường trung bình của ∆ABC
    ⇒ MD = AC : 2
    ⇒ AC = 2MD (1)

Do M và E đối xứng qua D
⇒ D là trung điểm của ME
⇒ ME = 2MD (2)

Từ (1) và (2) ⇒ AC = ME
Do AC // MD (cmt)
    ⇒ AC // ME

Tứ giác ACME có:
AC // ME (cmt)
AC = ME (cmt)
    ⇒ ACME là hình bình hành

Bài 4 Đề 15

Cho biết thang của một xe cứu hoả có chiều dài 13 m, chân thang cách mặt đất 3 m và cách tường của toà nhà 5 m. Tính chiều cao mà thang có thể vươn tới.

            a)                                                 b)

Đặt các điểm A, B, c, H như hình vẽ trên.
Áp dụng định lí Pythagore cho tam giác ABC vuông tại c, ta có:
$AB^2= AC^2+ BC^2.$
Suy ra: $AC^2= AB^2- BC^2 = 13^2 - 5^2$ = 169 - 25 = 144 = $12^2$.
Do đó AC = 12 m và AH = 12 + 3 = 15 (m).
Vậy chiều cao mà thang có thể vươn tới là 15 m.

Bài 5 Đề 15
    Thời gian tự học tại nhà của bạn Mai trong một tuần được biểu diễn trong biểu đồ đoạn thẳng dưới đây
    a) Ngày nào bạn Mai tự học nhiều nhất, ít nhất ?
    b) Thời gian bạn Mai tự học trong ngày thứ tư chiếm bao nhiêu phần trăm so với thừi gian tự học trong tuần?

GIẢI

a) Ngày học nhiều nhất: Thứ năm; ít nhất: Thứ sáu
b) Thời gian học trong ngày thứ tư chiểm phần trăm so với thời gian tự học trong tuần là:
    Tổng thời gian: 90+ 105 + 120+ 150 +60 = 525ph
    Thời gian học ngày thứ tu: 120 ph
    Tỉ lệ %
        120/525X 100 =