Đề 1
Bài 3 Đề 1
Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC.
Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh tứ giác ABDC là hình chữ nhật.
b)Trên tia đối của tia BA lấy điểm E sao cho BA =BE. . Chứng minh tứ giác BEDC là hình bình hành.
c) EM cắt BD tại K. Chứng minh EK = 2KM.
(Câu hỏi trong đề: Giải SBT Toán 8 CTST Bài 5. Hình chữ nhật – Hình vuông có đáp án)
TRẢ LỜI:

a) Xét tứ giác ABDC có: AM = MD (M ∈ AD); BM = MC (M ∈ BC).
Suy ra tứ giác ABDC là hình bình hành.
Ta lại có ˆBAC=90°BAC^=90° (do ∆ABC vuông tại A).
Do đó, tứ giác ABDC là hình chữ nhật.
b) Tứ giác ABDC là hình chữ nhật (theo câu a), suy ra AB = CD và AB // CD.
Do E đối xứng với A qua B nên B, A, E thẳng hàng và AB = BE.
Vì AB // CD nên BE // CD.
Vì AB = CD và AB = BE nên CD = BE.
Xét tứ giác BEDC có BE // CD và BE = CD nên là hình bình hành.
c) ∆AED có hai đường trung tuyến EM và DB cắt nhau tại K, nên K là trọng tâm của tam giác AED.
Suy ra EK=$\frac{2}{3}$EM và KM=$\frac{1}{3}$EM nên EK = 2KM.
Lý thuyết Hình chữ nhật – Hình vuông
I. Hình chữ nhật
Hình chữ nhật là tứ giác có bốn góc vuông.

*Tính chất
Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Nhận xét: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
*Dấu hiệu nhận biết
Nếu một tứ giác có ba góc vuông thì góc còn lại cũng là góc vuông và tứ giác đó là hình chữ nhật.
II. Hình vuông
Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
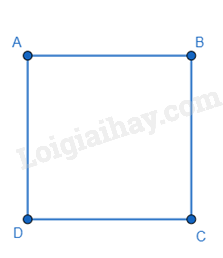
*Tính chất
Trong một hình vuông, hai đường chéo bằng nhau, vuông góc với nhau, cắt nhau tại trung điểm của mỗi đường và là các đường phân giác của các góc của hình vuông.
*Dấu hiệu nhận biết hình vuông
- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
- Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
- Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
Bài 4 Đề 1
Một cầu trượt có đường lên BA dài 5m, độ cao AC là 4m, độ dài DB là 9m, HD là 2m. Tính độ dài đường trượt tổng cộng ADH.
(Câu hỏi trong đề: Bài tập tuần Toán 7 Học kì 2 có đáp án !!)
Trả lời:
Để tính độ dài đường trượt tổng cộng ADH, ta cần tính độ dài các đoạn AB, BC, CD, DH.
- Độ dài đoạn AB: 5m
- Độ dài đoạn BC: Để tính độ dài đoạn BC, ta sử dụng định lý Pythagore trong tam giác vuông ABC:
$AC^2 + BC^2 = AB^2$
$4^2 + BC^2 = 5^2$
$BC^2 = 25 - 16$
$BC^2 = 9$
$BC = 3m$
$\Rightarrow$ CD = 9 - 3 = 6 (m)
- Độ dài đoạn DH: Độ dài đoạn DH đã được cho là 2m.
Tổng cộng, độ dài đường trượt ADH là:
ADH = AD + DH = 7,2 + 2 = 9,2 (m)
Vậy, độ dài đường trượt tổng cộng ADH là khoảng 9,2 (m) (làm tròn đến hàng đơn vị).
Bài 5 đề 1, bài 5 đề 2:
Biểu đồ dưới đây cho biết ti lệ mỗi loại trái cây bán được của một cửa hàng.
a) Lập bảng thống kê tương ứng với biểu đồ bên
Hãy chuyển đổi dữ liệu từ biểu đồ trên sang dạng bảng thống kê theo mẫu sau:
Trả lời
a) Bảng thống kê biểu diễn dữ liệu thống kê từ biểu đồ:
Bài 3 Đề 2
a) Chứng minh tứ giác ADHE là hình chữ nhật.
b) Trên tia đối của tia AC lấy điểm F sao cho AF=AE . Chứng minh tứ giác AFDH là hình bình hành.


Tứ giác ADHE có:
$\widehat{DAE}=90^0$ (gt)$\widehat{ADH}=90^0$ (HD$\bot$AB)
$\widehat{AEH}=90^0$ (HE$\bot$AC)
Do đó ADHE là hình chữ nhật (dấu hiệu nhận biết.)
b) Chứng minh tứ giác AFDH là hình bình hành.
Ta có AF = AE (gt)
AE = DH ( ADHE là hình chữ nhật )
$\Rightarrow$ AF = DH
Tứ giác AFDH có AF = DH
và AF//DH (ADHE là hình chữ nhật.)
$\Rightarrow$ Tứ giác AFDH là hình bình hành (dấu hiệu nhận biết)
Bài 4 Đề 2
Một viên bi lăn theo đoạn đường từ A đến D như hình vẽ (AB⊥BC,BC⊥CD).
Hãy tính khoảng cách AD. Biết rằng AB = 10m, BC = 12m, CD = 6m.
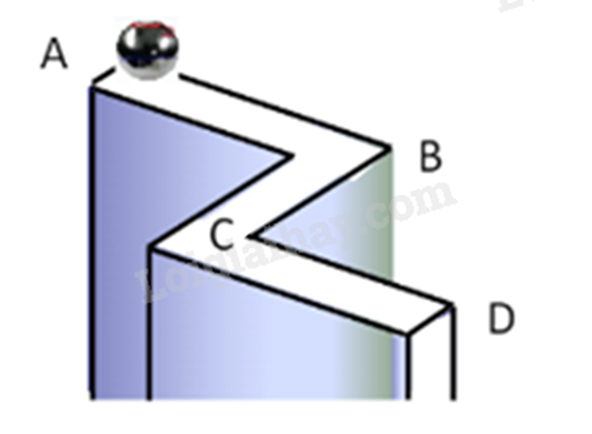
Phương pháp giải
Từ D vẽ Dx⊥CD cắt AB tại E.
Chứng minh BCDE là hình chữ nhật, sử dụng tính chất của hình chữ nhật để tính BE, suy ra độ dài AE.
Dựa vào định lí Pythagore để tính cạnh AD.
Lời giải
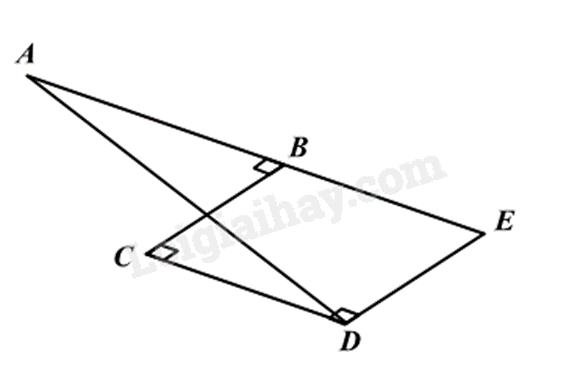
Từ D vẽ Dx⊥CD cắt AB tại E.
Mà BC⊥CD nên DE//BC
Vì AB⊥BC,BC⊥CD nên AB//CD.
Xét tứ giác BCDE có $\widehat{B}$ = $\widehat{C}$ = $\widehat{D}$ = $90^0$ nên BCDE là hình chữ nhật.
Suy ra DE = BC =12m; BE = CD = 6m; $\widehat{E}$ = $90^0$
Dẫn đến AE=AB+BE=10+6=16(m)
Áp dụng định lí Pythagore vào tam giác ADE vuông tại E, ta có:AD=$\sqrt{AE^2+DE^2}$=$\sqrt{16^2+12^2}=20$(m)
Vậy khoảng cách AD là 20m.
Bài 5 Đề 2:
Biểu đồ thể hiện sổ các con vật nuôi của các bạn trong lớp 8B

b) Con vật nào được nuôi nhiều nhất, ít nhất, là bao nhiêu?
a) Bảng thống kê:
b) Con vật nào được nuôi nhiều nhất, ít nhất, là bao nhiêu?
Trả lời
Con vật được nuôi nhiều nhất là cá (12 con). Con vật được nuôi ít nhất là mèo (5 con). Số cá nhiều gấp đôi số mèo
ĐỀ 3
Cho tam giác ABC cân tại A. Gọi H, D lần lượt là trung điểm của các cạnh BC và AB.
a/ Chứng minh rằng tứ giác ADHC là hình thang.
b/ Gọi E là điểm đối xứng với H qua D. Chứng minh rằng tử giác AHBE là hình chữ nhật.
c) Tia CD cắt AH tại M và cắt BE tại N. Chứng minh rằng tứ giác AMBN là hình bình hành.
TRẢ LỜI:
Phương pháp giải
a) Áp dụng dấu hiệu nhận biết của hình thang
b) Áp dụng dấu hiệu nhận biết của hình chữ nhật
c) Áp dụng dấu hiệu nhận biết của hình bình hành
a/ Chứng minh rằng tứ giác ADHC là hình thang.
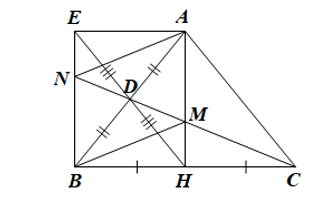
• Do ∆ABC cân tại A nên $\widehat{ABC}=\widehat{ACB}$ và AB = AC.
Vì AB = AC nên A nằm trên đường trung trực của BC.
Vì H là trung điểm của BC nên H nằm trên đường trung trực của BC.
Do đó AH là đường trung trực của BC nên AH ⊥ BC.
• Xét DAHB vuông tại H có HD là đường trung tuyến ứng với cạnh huyền AB nên bằng nửa cạnh huyền AB.
Do đó HD=DB=DA=$\frac{1}{2}$AB
• Tam giác DBH có DB = DH nên là tam giác cân tại D
Suy ra $\widehat{DBH}=\widehat{DHB}$ hay $\widehat{ABC}=\widehat{DHB}$
Lại có $\widehat{ABC}=\widehat{ACB}$ (chứng minh trên) nên $\widehat{DHB}=\widehat{ACB}$
Mà hai góc này ở vị trí đồng vị nên DH // AC.
• Xét tứ giác ADHC có DH // AC nên là hình thang.
b) Chứng minh rằng tử giác AHBE là hình chữ nhật.
Vì E đối xứng với H qua D (gt)
Suy ra D là trung điểm của HE
Xét tứ giác AHBE ta có:
Hai đường chéo HE và AB cắt nhau tại trung điểm D
Suy ra AHBE là hình bình hành
Mà $\widehat{AHB}$=$90^∘$ (cmt)
Suy ra AHBE là hình chữ nhật
Vì AHBE là hình chữ nhật (cmt)
Suy ra AH // BE và AH=BE
Xét ΔDEN và ΔDHM ta có:$\widehat{NED}=\widehat{DHM}$ (do BE // AH)
DE=DH (do D là trung điểm của HE)
$\widehat{EDN}=\widehat{MDH}$ (đối đỉnh)
Suy ra ΔDEN=ΔDHM (g-c-g)
Suy ra EN=MH (hai cạnh tương ứng)
Mà BE=AH (cmt)
Suy ra BE−EN=AH−MH
Suy ra NB=AM
Mà NB // AM (do EB // AH)
Suy ra AMBN là hình bình hành
Bài 5 Đề 3:
Số máy cày có trong năm xã được biểu diễn bằng biểu đồ dưới đây

a) Lập bảng thống kê tương ứng với biểu đồ trên.
b/ Trong tinh huống những xà có trên 20 máy cày cần đầu tư một trạm bảo trì và sửa chữa riêng, theo em đó có thể là những xã nào?
Trả lời
Phương pháp giải
Quan sát, phân tích biểu đồ và trả lời câu hỏi
Lời giải
a) Xã B có nhiều máy cày nhất (45 máy cày) và xã E có ít máy cày nhất (15 máy cày).
b) Có 2 xã có trên 20 máy cày, đó là xã B (45 máy cày) và xã C (25 máy cày)
Do đó hai xã này cần đầu tư một trạm bảo trì và sửa chữa riêng.
ĐỀ 4
Bài 3 Đề 4:
Cho tam giác ABC cân tại A. Kẻ đường cao AH. Gọi M là trung điểm cùa AB. Trên tia đối MH lấy điểm D sao cho MD = MH.

a) Chứng minh rằng tứ giác AHBD là hình chữ nhật.
b) Chứng minh tứ giác ACHD là hình bình hành.
GIẢI
a) Chứng minh rằng tứ giác AHBD là hình chữ nhật.
Tứ giác AHBD có:
MA = MB (gt)
MH = MD (gt)
Tứ giác AHBD có hai đường chéo cắt nhau tại trung điểm M , là hình bình hành.
Hình bình hành AHBD có góc H = $90^0$, là hình chữ nhật.
b) Chứng minh tứ giác ACHD là hình bình hành.

AD = HB (t/c hình chữ nhật AHBD)
mà HB = HC (gt)
$\Rightarrow$ AD = HC
mà AD // HC (t/c hình chữ nhật AHBD)
nên tứ giác ACHD là hình bình hành ( hai cạnh đối // và bằng nhau)
(Từ đây có thể c/m AC // DH ; AC = DH)
Bài 4 Đề 4:

GIẢI

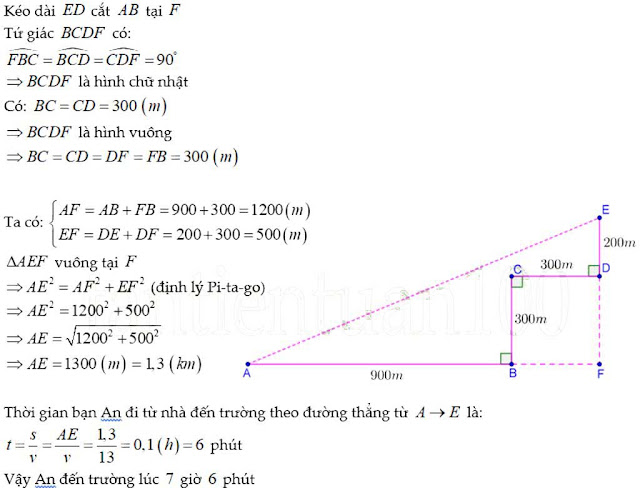
a) Tính AB + BC + CD + DE + EG + GH.
Kéo dài cạnh AB, lấy BM = CD, MI = EG.
Kéo dài cạnh HG, lấy GN = ED; NI = CB.
Tứ giác BCDM có 2 góc vuông (B và C) là hình thang vuông, có BM = CD (gt) nên BCDM là hình chữ nhật.
C/m tương tự, ta có: các tứ giác MEGI, BCNI, NDEG là các hình chữ nhật.
Suy ra: BC = NI; CD = BM; EG = MI;
Do đó AB + BC + CD + DE + EG + GH
= AB + CD + EG + BC + DE + GH
= AB + BM + MI + IN + NG + GH
= 1000 + 600 + 400 + 700 + 300 + 500 = 3.500(m)
= AI + IH = 3.500(m)
AI = 1000 + 600 + 400 = 2 000 (m) = 2 (km)
IH = 700 + 300 +500 = 1 500 (m) = 1,5 (km)
Xét tam giác vuông IHA, theo định lý Pythagore, ta có:
$AH^2 = AI^2 + IH^2$
= $2^2 + {1,5}^2$
= 4 + 2,25 = 6, 25
AH = $\sqrt{6, 25}$ = 2,5 (km)
Biết vận tốc 25km/h
Vậy thời gian đi hết đoạn đường này là
$\frac{2,5}{25}$= $\frac{1}{10}$ (giờ) = 6 phút
Bạn Nam đến trường lúc 6H35 + 6 ph = 6H41.
Bài 5 Đề 4:
Biểu đồ biểu diễn chỉ số tăng trưởng của đàn trâu Việt Nam qua các năm.

Lập bảng thống kẻ tương ứng với biểu ở bên.
Cho biết đàn trâu Việt Nam năm 1990 là 2854,1 nghìn con. Tính số lượng đàn trâu của Việt Nam năm 2000.
Biểu đồ biểu diễn chỉ số tăng trưởng của đàn trâu Việt Nam qua các năm.
a) Lập bảng thống kê tương ứng với biểu đồ bên.
b) Cho biết đàn trâu Việt Nam năm 1990 là 2854,1 nghìn con. Tính số lượng đàn trâu của Việt Nam năm 2000.

|
Năm |
1990 |
1995 |
2000 |
2002 |
|
Chỉ số trâu |
100 |
103,8 |
101,5 |
98,6 |
Chỉ số trâu năm 2000 là 101,5
Số trâu năm 2000 là $\Large{\frac{2854,1 \times {101,5}}{100}}$ = ?
Câu 3 Đề 4:
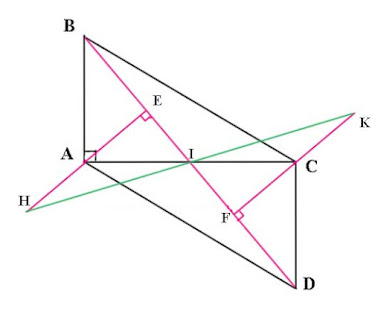
Cho hình bình hành ABCD có AB = 2AD. Gọi E và F lần lượt là trung điểm của AB và CD, / là giao điểm của AF và DE, K là giao điểm cùa BF và CE.
a) Chứng minh rằng tứ giác AECF là hình bình hành.
b) Tứ giác AEFD là hình gì? Vì sao?
c) Chứng minh tứ giác EIFIC là hình chữ nhật.
d) Tìm điều kiện của hình bình hành ABCD đề tứ giác EIFK là hình vuông.a)
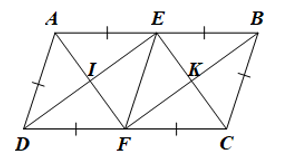
• Do ABCD là hình bình hành nên AB = CD và AB // CD.
Vì E là trung điểm của AB nên $EA=EB=\frac{1}{2}AB$ .
F là trung điểm của CD nên $FC=FD=\frac{1}{2}CD$
Mà AB = CD (chứng minh trên).
Do đó EA = EB = FC = FD.
• Xét tứ giác AECF có EA = FC và EA // FC (do AB // CD)
Suy ra AECF là hình bình hành.
Giải thích
a) Để chứng minh tứ giác AECF là hình bình hành, ta cần chứng minh hai cặp cạnh đối song song và bằng nhau. Trong hình bình hành ABCD, AB song song và bằng CD.
Vì E và F là trung điểm của AB và CD, nên AE = EB và CF = FD.
Do đó, AE = CF (vì AB = CD).
Mặt khác, vì AB song song với CD, nên AE song song với CF.
Tương tự, AF song song và bằng CE.
Vậy AECF là hình bình hành.
b) Tứ giác AEFD là hình thang cân.
Điều này có thể được chứng minh bằng cách xem xét các cặp cạnh đối và góc.
Trong hình bình hành ABCD, AB song song với CD, và do đó AE song song với DF.
Vì E và F là trung điểm của AB và CD, nên AE = 1/2 AB và DF = 1/2 CD.
Vì AB = CD, nên AE = DF.
Do đó, AEFD là hình thang cân.
c) Để chứng minh tứ giác EIFK là hình chữ nhật, ta cần chứng minh rằng nó có các góc vuông.
Vì AECF là hình bình hành, nên góc AFE và góc AEC là góc so le trong và bằng nhau.
Tương tự, góc AFB và góc AED cũng bằng nhau.
Khi AF cắt DE tại I và BF cắt CE tại K, góc EIF và góc EKF là các góc so le trong và bằng nhau.
Do đó, EIFK là hình chữ nhật.
d) Để EIFK là hình vuông, cần có điều kiện là EIFK không chỉ là hình chữ nhật mà còn là hình có các cạnh bằng nhau.
Điều này xảy ra khi hình bình hành ABCD là hình thoi, tức là AB = AD.
Khi đó, AE = DE và BF = CF, và do đó, IF = EK. Vì EIFK đã là hình chữ nhật, nếu IF = EK, thì nó cũng là hình vuông.
Câu 4 Đề 4.
Nhà bạn Lan (trên hình vẽ) cách nhà bạn Thanh (trên hình vẽ) 2km và cách trường học (trên hình vẽ) 12km. Biết rằng 3 vị trí: nhà Thanh, nhà Lan và trường học là 3 đỉnh của một tam giác vuông (xem hình vẽ). Hãy tính khoảng cách từ nhà Thanh đến trường học.

GIẢI
Xét △ABC vuông tại B, có:
$AB^2+BC^2=AC^2$ (Định lý Pythagore)
$2^2+12^2=AC^2$
$AC^2$=148
⇒AC=$\sqrt{148}$=2$\sqrt{37}$(km)
ĐỀ 6
Bài 3 Đề 6
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Kẻ MD vuông góc AB lại D, MF vuông góc AC tại F.
a) Chứng minh: Tứ giác ADMF là hình chữ nhật.
b) Vẽ E dối xứng M qua D. CM: tứ giác ACME là hình bình hành.
Giải:
$\widehat{MFA} = \widehat{EDA} = \widehat{DAF} = 90^{\circ}$
Vậy tứ giác AEMF là hình chữ nhật.
$\Rightarrow$ AF = FC.
Vậy tứ giác ACME là hình bình hành.
Bài 4 Đề 6:
Một người dạng ở trên một cái tháp có chiều cao 80m nhìn xuống một con dường chạy thẳng đến chân tháp (địa diễm B). Anh ta nhìn thấy 1 chiếc xe máy ở địa diễm D cách A 170m. Mười hai phút sau lại nhìn thấy nó ở địa điểm C cách A 100m. Hỏi sau bao nhiều phút nữa thì xe máy đến chân tháp? Cho biết vận tốc xe này không đổi. (kết quả làm tròn tới hàng đơn vị ).
Ta có:
AB = 80m (gt)
AD = 170m (gt)
AC = 100m (gt)
Thời gian từ D đến C:
12 phút = 720 giây (gt)
Xét ABD vuông tại B
Ta có: AB² + BD² = AD² ( Pythagore)
=> DB = $\sqrt{AD² - AB²} = \sqrt{170² - 80² }$= $\sqrt{(170 - 80)(170 + 80)}$ = $\sqrt{90 \times {250}}$ = $\sqrt{22.500}$ = 150 (m)
Xét ABC vuông tại B
Ta có: AB² + BC² = AC² (Pytago)
=> BC = $\sqrt{AC² - AB²}$ = $\sqrt{100² - 80²}$ = 60 (m)
mà DC = BD - BC = 150 - 60 = 90 (m)
Vận tốc của xe là
V = S/t = DC/t = 90/720 = 0,125 m/s
Do vận tốc không thay đổi nên
Thời gian xe đến chân tháp
V = S/t $\Rightarrow$ t = S/V = BC/V = 60/0,125 = 480 giây = 8 phút
Bài 3 Đề 7
Cho ABC nhọn có AB <AC và đường cao AH. Gọi M, N lần lượt là trung điểm của AB và AC.Trên tia HN lấy điểm E sao cho NE = NH.a) Chứng minh: Tứ giác AHCE là hình chữ nhật.
b) Gọi O là giao điểm của EA và L/M.Trên tia HC lấy điểm 0 sao cho HO = HB. Chứng minh: Tứ giác AOHQ Là hình bình hành
Bài 4 đề 7
Một chiếc xe cứu hỏa có thang trên nóc
xe để tiếp cận những vị trí cao cần cứu hộ. Hãy tính vị trí cao nhất mà thang
trên nóc xe có thể tiếp cận trong hình vẽ dưới đây?
$AB^{2} = BC^{2} - AC^{2} = 20^{2} + 12^{2}$ =256
Khoảng cách từ mặt đất đến vị trí cao nhất mà thang có thể vươn tới là:
AF = AB + BF = 16 + 2,5 = 18,5 m
Bài 5 Đề 7
Biểu đồ cột ở hình vẽ bên biếu diễn tỉ lệ về giá trị đạt được của khoáng sản xuất khẩu nước ngoài của nước ta (tính theo tỉ số phần trăm) .
a) Lập bảng thống kê tỉ lệ về giá trị đạt được của khoáng sản xuất khẩu nước ngoài của nước ta
b) Dầu có tỉ lệ phần trăm xuất khẩu nước ngoài cao nhất, vàng có tỉ lệ phần trăm xuất khẩu nước ngoài thấp nhất.
Bài 5 Đề :
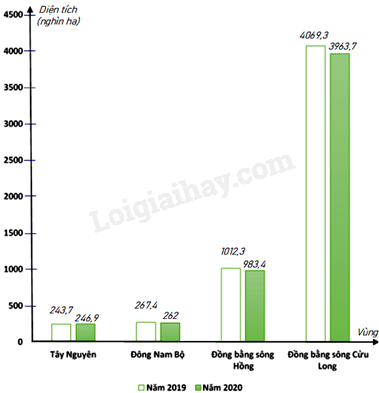
Biểu đồ cột kép ở hình bên biểu diễn diện tích gieo trồng lúa trong các năm 2019; 2020 cua các vùng : Tây Nguyên; Đông Nam Bộ; Đồng bằng sông Hồng; Đồng bằng sông Cừu Long . (đơn vị: nghìn ha) (Nguồn : Niên giám thống kê 2021).
a) Lập bảng thống kê tỉ số diện tích gieo trồng lúa của năm 2019 và diện tích gieo trồng lúa của năm 2020 của các vùng nói trên ( viết tỉ số ở dạng số thập phân và làm tròn kết quả đến hàng phần trăm).
Đề 8
Bài 3 Đề 8
Cho tam giác ABC cân tại A . Gọi M là trung điểm của AB. Vẽ MN // BC(N $\in$AC)
Chứng minh rằng tứ giác BMNC là hình thang cân.
Bài 4 Đề 8:
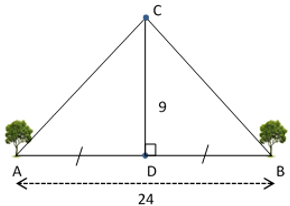
Hai cây A và B được trồng dọc trên đường, cách nhau 24m và cách đều cột đèn D. Ngôi trường C cách cột đèn D 9m theo hướng vuông góc với đường (xem hình vẽ).
b) Lựa chọn và vẽ biểu đồ biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này.
a) Biểu đồ so sánh số học sinh tham gia hai câu lạc bộ ở từng lớp:

b) Để biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này ta nên dùng biểu đồ hình quạt tròn.
b) Để biếu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này ta dùng biểu đồ hình quạt tròn.
Tổng số học sinh tham gia hai câu lạc bộ của khối 8 là:
8 + 16 +12+ 4 + 10 + 8 + 5 + 8 = 71 (học sinh).
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8A là: 8 + 16 = 24 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8A so với số các học sinh khối 8 tham gia hai câu lạc bộ là: $\frac{24}{71}$ $\approx$33,8% .
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8B là: 12 + 4 = 16 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8B so với số các học sinh khối 8 tham gia hai câu lạc bộ là: $\frac{16}{71}$ $\approx$ 22,5%
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8C là: 10 + 8 = 18 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8C so với số các học sinh khối 8 tham gia hai câu lạc bộ là: $\frac{18}{71}$ $\approx$ 25,4%.
• Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8C so với số các học sinh khối 8 tham gia hai câu lạc bộ là:
100% - 33,8% - 22,5% - 25,4% = 18,3%.
Biểu đồ hình quạt tròn biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này.
Đề 11
Bài 4 Đề 11
Học sinh trượt trên máng trượt từ C đến B với vận tốc trung bình 5m/s thì sao 4 giây sẽ xuống mặt đất. Cho biết khoảng cách từ trụ (CD) đến chân máng trước (B) dài 16m.
Tính độ dài quãng đường AB: AB = CB + DB = 20 + 16 = 36 (m)
Tính độ dài quãng đường AC: AC = $\sqrt{AB^{2} - BC^{2}}$− = $\sqrt{36^{2} - 20^{2}}$ = 32 (m)
Đổi đơn vị độ dài AC sang cm: AC = 32 m = 3200 cm
Tính số bậc thang của cầu thang: Số bậc thang = AC/chiều cao mỗi bậc thang = 3200/15 = 213,33 ≈ 214 (bậc)
1. xét tứ giác AHBD có:
MA = MB (gt)
MH = MK (gt)
$\widehat{AHB}=90^0$
Tứ giác AHBD có hai đường chéo cắt nhau tại trung điểm mỗi đường, là hình bình hành
Hình bình hành có một góc vuông, là hình chữ nhật
=> tứ giác ADHE Là hình chữ nhật
b) Chứng minh tứ giác ADHE là hình bình hành
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Gọi M là trung điểm của AB. Trên tia đối của tia MH lấy điểm D sao cho MD = MH
a) Tứ giác AHBD là hình gì? Vì sao?
b) Gọi E là điểm đối xứng với B qua điểm H. Chứng minh ADHE là hình bình hành.
c) Kẻ EF⊥AC; HK⊥AC (F,K∈AC). Chứng minh rằng AH = HF.
d) Gọi I là trung điểm của EC. Chứng minh HF⊥FI
Đề 10
Bài 4 Đề 10
Để đón được một người khách, một xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3 km đến điểm B thì rẽ vuông góc sang trái, chạy được 3 km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1 km nữa thì gặp người khách tại điểm D (H.9.38). Hỏi lúc đầu, khoảng cách từ chỗ người lái xe đến người khách là bao nhiêu kilômét?
Suy ra AD = 5km.
Bài 5 Đề 10
Số sản phẩm bán được của
một công ty trong sáu tháng đầu năm được biểu diễn trong biểu đồ (hình bên).
a) Chuyển dữ liệu trong biểu đồ sang dạng
bảng thống kê tương ứng với biểu đồ bên.
b) Phân tích biểu đồ thống kê hình bên để
tìm tháng bán được nhiều hàng nhất và tháng bán được ít hàng nhất.
a) Chuyển dữ liệu trong biểu đồ sang dạng bảng thống kê tương ứng với biểu đồ bên.
|
Tháng |
1 |
2 |
3 |
4 |
5 |
6 |
|
Sản phẩm |
2 |
4 |
6 |
3 |
2 |
7 |
b) Phân tích biểu đồ thống kê hình bên để tìm tháng bán được nhiều hàng nhất và tháng bán được ít hàng nhất.
Tháng bán được nhiều nhất là tháng 7
Tháng bán được ít nhất là tháng 1 và tháng 5
Bài 3 Đề 11
Cho tam giác ABC vuông tại A (AB>AC). Gọi M là trung điểm của BC. Từ M kẻ MH vuông góc AB, MN vuông góc AC
a) Chứng minh tứ giác MHAN là hình chữ nhật
b) Trên tia AM lấy điểm D sao cho MA = MD. Chứng minh tứ giác ABDC là hình chữ nhật
$\widehat{A}=\widehat{N}= \widehat{H}= 90^0$
Cho tam giác ABC vuông tại A (AB <AC), từ điểm M là trung điểm BC, kẻ $MD\perp{AB}, (D \in{AB})$
GIẢI
Mặt cắt đứng của sân khấu ngoài trời có mái che ở Hình 10 được mô tả như hình vẽ dưới đây.
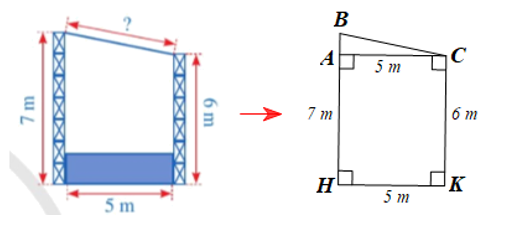
Ta có: AB = BH – AH = BH – CK = 7 – 6 = 1 (m).
Xét tam giác ABC vuông tại A, theo định lí Pythagore ta có:
$BC^2 = AB^2 + AC^2 = 1^2 + 5^2 $= 1 + 25 = 26.
Suy ra BC=$\sqrt{26}$ = 5,099019514...≈5,10(m)
Vậy chiều dài của mái che sân khấu đó khoảng 5,10 mét.
Lựa chọn dạng biểu đồ thích hợp để biểu diễn các thông tin từ bảng thống kê sau:
Biểu đồ hình quạt tròn biểu diễn tỉ số
phần trăm số học sinh chọn môn thể thao ưa thích của học sinh lớp 8B:
Lập bảng thống kê tương ứng với Biểu đồ bên. ; Từ năm 2000 đến 2010, tuổi thọ trung bình của người dân Việt Nam tăng bao nhiêu phần trăm.
|
Năm |
1980 |
1985 |
1990 |
1995 |
2000 |
2006 |
2010 |
2015 |
2018 |
|
Tuổi |
67 |
69 |
71 |
72 |
73 |
74 |
75 |
75 |
75 |
b) Chứng minh: $EB^2 - EC^2 =AB^2$
a) (TH) Chứng minh: AHED là hình thang vuông. Ta có: AH ± BC tại H
DE ± BC lại E
o AH//DE
<=> Tứ giác AHED là hỉnh thang
Mà A27E=90°
<=> Tứ giác AHED là hỉnh thang vuông
b) (VD) Chứng minh: EB2 - EC2= AB2.
Ta có: EB2-EC2
= BD2-DE2-(DC2-DE2)
= BD2-AD2(vì AD = DC)
= AB2
Vậy EB2-EC2 = AB2
Bài 4 Đề 14

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Kẻ MD vuông góc với AB tại D.
a) Chứng minh: Tứ giác ADMC là hình thang vuông.
b) Vẽ E đối xứng M qua D. Chứng minh tứ giác ACME là hinh chữ nhật.
GIẢI
⇒ AB ⊥ AC
Mà MD ⊥ AB (gt)
⇒ AC // MD
⇒ ADMC là hình thang
Mà ∠CAD = 90⁰ (∆ABC vuông tại A)
⇒ ADMC là hình thang vuông
b) ∆ABC có:
M là trung điểm của BC (gt)
MD // AC (cmt)
⇒ D là trung điểm của AB
⇒ MD là đường trung bình của ∆ABC
⇒ MD = AC : 2
⇒ AC = 2MD (1)
Do M và E đối xứng qua D
⇒ D là trung điểm của ME
⇒ ME = 2MD (2)
Từ (1) và (2) ⇒ AC = ME
Do AC // MD (cmt)
⇒ AC // ME
Tứ giác ACME có:
AC // ME (cmt)
AC = ME (cmt)
⇒ ACME là hình bình hành
Bài 3 Đề 16
Một người chạy trên một dốc có độ dài AC = 10 mét. Biết đỉnh dốc đó cao 4 mét (Hình 1). Tính khoảng cách từ A đến B. (Làm tròn kết quả đến hàng đơn vị).
Câu 3 Đề 16.
Phương pháp nào là phù họp để thu
thập dừ liệu và lập bảng thống kc về số trường THCS cua 6 tinh, thành phố khu vực
Đỏng Nam Bộ năm 2022,
A.Thu thập từ những nguồn có sẵn như
sách, báo, internet.
B. Quan sát trực tiếp
C. Lập phiếu thăm dò.
D. Làm thí nghiệm
Đề bài
Hãy sử dụng phương pháp thích hợp để thu
thập dữ liệu và lập bảng thống kê dân số các tỉnh khu vực miền Đông Nam Bộ của
Việt Nam
TRẢ LỜI:
Giải bởi Vietjack
Ta dùng phương pháp thu thập từ nguồn có
sẵn qua mạng Internet để thu thập dữ liệu về dân số các tỉnh khu vực miền Đông
Nam Bộ của Việt Nam, chẳng hạn truy cập trang web https://www.gso.gov.vn/dan-so/ (Tổng cục Thống kê).
Bảng thống kê dân số (năm 2021) các tỉnh
khu vực miền Đông Nam Bộ của Việt Nam:

















































0 Comments:
Đăng nhận xét