Bài 3 Đề 12
Cho tam giác ABC vuông tại A (AB <AC), từ điểm M là trung điểm BC,
kẻ $MD\perp{AB}$; $(D\in{AB})$
a) Chứng minh: tứ giác MDAE là hình chữ nhật.
b) Trên tia đối của tia DM, lấy điểm K sao cho DM = DK. Chứng minh: AKDE là hình bình hành.
GIẢI
a) Chứng minh: tứ giác MDAE là hình chữ nhật.

Xét tứ giác MDAE, ta có:
$\widehat{A}$=$\widehat{D}$=$\widehat{E}$= $90^0$a) Chứng minh: tứ giác MDAE là hình chữ nhật.
b) Trên tia đối của tia DM, lấy điểm K sao cho DM = DK. Chứng minh: AKDE là hình bình hành.
GIẢI
a) Chứng minh: tứ giác MDAE là hình chữ nhật.

Xét tứ giác MDAE, ta có:
Tứ giác có 3 góc vuông là hình chữ nhật.
b) Chứng minh: AKDE là hình bình hành.

Xét tứ giác AKDE, ta có:
KD = DM (gt)
mà DM = AE ( t/c hình chữ nhật MDAE)
Suy ra KD = AE.
mà DM // E nên KD // AE
Vậy AKDE có 2 cạnh đối song song và bằng nhau. AKDE là hình bình hành.
Bài 4 Đề 12
Hình bên dưới mô tả mặt cắt đứng của một sân khấu ngoài trời có mái che. Chiều cao của khung phía trước khoảng 7 m, chiều cao của khung phía sau là 6 m, hai khung cách nhau một khoảng là 5 m. Chiều dài của mái che sân khấu đó là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
GIẢI

Mặt cắt đứng của sân khấu ngoài trời có mái che ở Hình 10 được mô tả như hình vẽ dưới đây.
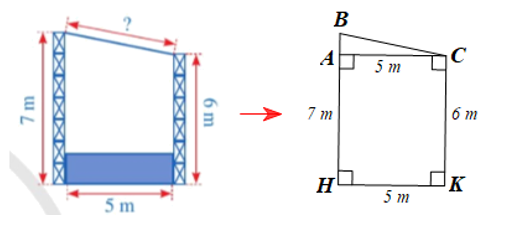
Ta có: AB = BH – AH = BH – CK = 7 – 6 = 1 (m).
Xét tam giác ABC vuông tại A, theo định lí Pythagore ta có:
= 1 + 25 = 26.
Suy ra BC= = 5,099019514...≈5,10(m)
Vậy chiều dài của mái che sân khấu đó khoảng 5,10 mét.
GIẢI

Mặt cắt đứng của sân khấu ngoài trời có mái che ở Hình 10 được mô tả như hình vẽ dưới đây.

Ta có: AB = BH – AH = BH – CK = 7 – 6 = 1 (m).
Xét tam giác ABC vuông tại A, theo định lí Pythagore ta có:
= 1 + 25 = 26.
Suy ra BC= = 5,099019514...≈5,10(m)
Vậy chiều dài của mái che sân khấu đó khoảng 5,10 mét.
Bài 5 Đề 12




0 Comments:
Đăng nhận xét