Đề bài
Bài 1 (2 điểm)
a) Phân tích đa thức sau thành nhân tử: \(x\left( {x - y} \right) + 2\left( {x - y} \right)\)
b) Tính nhanh giá trị của biểu thức: \({x^2} - 6{\rm{x}}y + 9{y^2}\) tại \(x = 16,\,y = 2\)
c) Tìm x, biết: \(2x\left( {x - 5} \right) - x\left( {2x + 3} \right) = 26\)
Bài 2 (2 điểm)
a) Rút gọn biểu thức: \(\dfrac{{{x^2} + xy}}{{{x^2} - {y^2}}}\)
b) Thực hiện phép tính: \(\dfrac{{4x + 12}}{{{{\left( {x + 1} \right)}^2}}}:\dfrac{{3\left( {x + 3} \right)}}{{x + 1}}\)
c) Thực hiện phép tính: \(\dfrac{4}{{x + 2}} + \dfrac{3}{{x - 2}} + \dfrac{{ - 5x - 2}}{{{x^2} - 4}}\)
Bài 3 (1,5 điểm)Cho hai đa thức \(A = 2{x^2} + 3x + 3\) và \(B = 2x - 1\).
a) Thực hiện phép chia A cho B.
b) Tìm các giá trị nguyên của x để giá trị của đa thức A chia hết cho giá trị của đa thức B.
Bài 4 (4 điểm)Cho \(\Delta ABC\) cân tại A. Gọi \(H,\,K\) lần lượt là trung điểm của \(BC\) và \(AC\).
a)Chứng minh tứ giác \(ABHK\) là hình thang.
b)Trên tia đối của tia \(HA\) lấy điểm \(E\) sao cho \(H\) là trung điểm của cạnh \(A{\rm{E}}\). Chứng minh tứ giác \(ABEC\) là hình thoi.
c) Qua A vẽ đường thẳng vuông góc với \(AH\) cắt tia \(HK\) tại \(D\). Chứng minh \(A{\rm{D}} = BH\).
d) Vẽ \(HN \bot AB\left( {N \in AB} \right)\), gọi I là trung điểm của AN. Trên tia đối của tia BH lấy điểm M sao cho B là trung điểm của HM. Chứng minh: \(MN \bot HI\)
Bài 5 (0,5 điểm)
Cho \(x,y,z\) là ba số thỏa mãn điều kiện: \(4{x^2} + 2{y^2} + 2{{\rm{z}}^2} - 4xy - 4x{\rm{z}} + 2yz - 6y - 10{\rm{z}} + 34 = 0\)
Tính: \(S = {\left( {x - 4} \right)^{2017}} + {\left( {y - 4} \right)^{2017}} + {\left( {z - 4} \right)^{2017}}\)
LG bài 1
Lời giải chi tiết:
\(\begin{array}{l}a)\,\,x\left( {x - y} \right) + 2\left( {x - y} \right) = \left( {x - y} \right)\left( {x + 2} \right).\\b)\,\,{x^2} - 6xy + 9{y^2} = {x^2} - 2.x{\rm{.3}}y + {\left( {3y} \right)^2} = {\left( {x - 3y} \right)^2}\end{array}\)
Thay \(x = 16,\,y = 2\)vào đa thức trên ta được: \({\left( {x - 3y} \right)^2} = {\left( {16 - 3.2} \right)^2} = {10^2} = 100\).
\(\begin{array}{l}c)\,\,2x\left( {x - 5} \right) - x\left( {2x + 3} \right) = 26\\ \Leftrightarrow 2{x^2} - 10x - 2{x^2} - 3x = 26\\ \Leftrightarrow - 13x = 26\\ \Leftrightarrow x = - 2.\end{array}\)
Vậy \(x = - 2.\)
LG bài 2
Lời giải chi tiết:
\(a)\,\,\dfrac{{{x^2} + xy}}{{{x^2} - {y^2}}} = \dfrac{{x\left( {x + y} \right)}}{{\left( {x + y} \right)\left( {x - y} \right)}} = \dfrac{x}{{x - y}}\)
\(b)\,\,\dfrac{{4x + 12}}{{{{\left( {x + 1} \right)}^2}}}:\dfrac{{3\left( {x + 3} \right)}}{{x + 1}} = \dfrac{{4\left( {x + 3} \right)}}{{{{\left( {x + 1} \right)}^2}}}.\dfrac{{x + 1}}{{3\left( {x + 3} \right)}} = \dfrac{4}{{3\left( {x + 1} \right)}}\)
\(\begin{array}{l}c)\,\,\dfrac{4}{{x + 2}} + \dfrac{3}{{x - 2}} + \dfrac{{ - 5x - 2}}{{{x^2} - 4}} = \,\dfrac{4}{{x + 2}} + \dfrac{3}{{x - 2}} + \dfrac{{ - 5x - 2}}{{\left( {x + 2} \right)\left( {x - 2} \right)}}\\ = \dfrac{{4\left( {x - 2} \right) + 3\left( {x + 2} \right) - 5x - 2}}{{\left( {x + 2} \right)\left( {x - 2} \right)}} = \dfrac{{4x - 8 + 3x + 6 - 5x - 2}}{{\left( {x + 2} \right)\left( {x - 2} \right)}}\\ = \dfrac{{2x - 4}}{{\left( {x + 2} \right)\left( {x - 2} \right)}} = \dfrac{{2\left( {x - 2} \right)}}{{\left( {x + 2} \right)\left( {x - 2} \right)}} = \dfrac{2}{{x + 2}}.\end{array}\)
LG bài 3
Lời giải chi tiết:
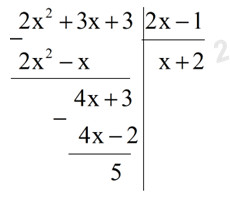
Để A chia hết cho B \( \Leftrightarrow 5 \vdots \left( {2x - 1} \right) \Leftrightarrow \left( {2x - 1} \right) \in U\left( 5 \right) \Leftrightarrow \left( {2x - 1} \right) \in \left\{ { \pm 1;\; \pm 5} \right\}.\) Ta có:
|
\(2x - 1\) |
1 |
-1 |
5 |
-5 |
|
\(x\) |
1 |
0 |
3 |
-2 |
Vậy \(x \in \left\{ {1;0;3; - 2} \right\}\) thì \(A\) chia hết cho \(B\).
LG bài 4
Lời giải chi tiết:
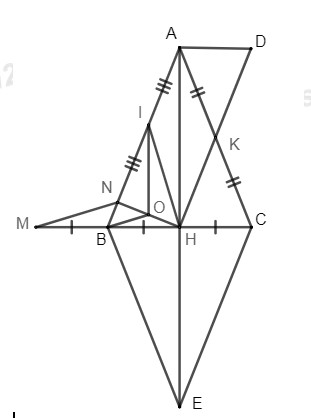
a)Xét \(\Delta ABC\) có: \(H,\,K\) lần lượt là trung điểm của \(BC\) và \(AC\) (gt)
\( \Rightarrow HK\) là đường trung bình của \(\Delta ABC\) (dấu hiệu nhận biết đường trung bình của tam giác)
\( \Rightarrow HK//AB\) (tính chất đường trung bình của tam giác)
\( \Rightarrow \) tứ giác \(ABHK\) là hình thang (dhnb)
b)Xét tứ giác\(ABEC\) có:\(H\) là trung điểm của \(A{\rm{E}}\) và \(BC\) (gt) nên suy ra tứ giác \(ABEC\) là hình bình hành (dhnb)
Lại có, \(\Delta ABC\) cân tại \(A\;\left( {gt} \right) \Rightarrow AB = AC\) (tính chất tam giác cân)
\( \Rightarrow \) Hình bình hành \(ABEC\) có hai cạnh bên bằng nhau nên là hình thoi (dhnb)
c)Vì \(\Delta ABC\) cân tại \(A\) (gt), mà \(AH\) là trung tuyến
\( \Rightarrow \)\(AH\) cũng là đường cao của \(\Delta ABC\)
\( \Rightarrow AH \bot BC\)
Mà \(AD \bot AH\left( {gt} \right) \Rightarrow AD//BH\;\;\left( { \bot AH} \right)\)
Lại có: \(AB//DH\)(do \(D,\,H,\,K\) thẳng hàng)
\( \Rightarrow \) Tứ giác \(ADHB\) là hình bình hành (dhnb)
\( \Rightarrow AD = BH\) (tính chất)
d)Gọi \(O\) là trung điểm của \(HN\) và \(I\) là trung điểm của \(AN\left( {gt} \right) \Rightarrow I{\rm{O}}\) là đường trung bình của \(\Delta ANH\) (dhnb)
\( \Rightarrow I{\rm{O}}//AH\) (tính chất)
Mà \(AH \bot BC \Rightarrow OI \bot BC\) hay \(OI\) là đường cao của tam giác \(BIH.\)
Xét \(\Delta BIH\) có đường cao HN và IO cắt nhau tại O nên O là trực tâm của \(\Delta IBH\)
\( \Rightarrow BO\) là đường cao của \(\Delta IBH\)
Hay \(BO \bot IH.\;\;\;\left( 1 \right)\)
Xét \(\Delta MNH\) có: \(B\)là trung điểm của \(MH,\;\;O\) là trung điểm của \(NH.\)
\( \Rightarrow BO\) là đường trung bình của \(\Delta MNH\)\( \Rightarrow BO//MN\) (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra \(MN \bot HI\) .
LG bài 5
Lời giải chi tiết:
\(\begin{array}{l}\;\;\;\;\;4{x^2} + 2{y^2} + 2{{\rm{z}}^2} - 4xy - 4{\rm{xz}} + 2yz - 6y - 10z + 34 = 0\\ \Leftrightarrow \left( {4{x^2} - 4xy + {y^2} + 2yz + {z^2} - 4xz} \right) + \left( {{y^2} - 6y + 9} \right) + \left( {{z^2} - 10z + 25} \right) = 0\\ \Leftrightarrow {\left( {2x - y - z} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 5} \right)^2} = 0\end{array}\)
Ta có: \(\left\{ \begin{array}{l}{\left( {2{\rm{x}} - y - z} \right)^2} \ge 0\\{\left( {y - 3} \right)^2} \ge 0\\{\left( {z - 5} \right)^2} \ge 0\end{array} \right. \Rightarrow {\left( {2x - y - z} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 5} \right)^2} \ge 0\,\forall x,\,y,\,z\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}2x - y - z = 0\\y - 3 = 0\\z - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\\z = 5\end{array} \right.\)
Thay \(x = 4,\,y = 3,\,z = 5\) vào \(S\) ta có:
\(S = {\left( {x - 4} \right)^{2017}} + {\left( {y - 4} \right)^{2017}} + {\left( {z - 4} \right)^{2017}} \)\(\,= {\left( {4 - 4} \right)^{2017}} + {\left( {3 - 4} \right)^{2017}} + {\left( {5 - 4} \right)^{2017}} = {\left( { - 1} \right)^{2017}} + {1^{2017}} = 0\).
Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 8 tại Tuyensinh247.com
Loigiaihay.com

0 Comments:
Đăng nhận xét