Định lí tổng các góc của một tứ giác

 1. Công thức 

Tứ giác ABCD có $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$

2. Ví dụ minh hoạ

Ví dụ 1. Cho tứ giác ABCD có $\hat{A}=70°$, $\hat{B}=100°$. Các tia phân giác của góc $\hat{C}$ và $\hat{D}$ cắt nhau tại O. Tính số đo $\widehat{COD}$.

Hướng dẫn giải

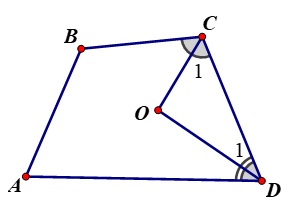
Áp dụng Định lí tổng các góc của tứ giác bằng 360°ta có:

$\hat{A}+\hat{B}+\widehat{BCD}+\widehat{CDA}=360°$

Suy ra $\widehat{BCD}+\widehat{CDA}=360°-\left(\hat{A}+\hat{B}\right)$

$\widehat{BCD}+\widehat{CDA}=360°-\left(70°+100°\right)=190°$.

Vì CO, DO lần lượt là tia phân giác của $\widehat{BCD}$ và $\widehat{CDA}$ nên:

${\hat{C}}_1=\frac{1}{2}\hat{C}$, ${\hat{D}}_1=\frac{1}{2}\hat{D}$.

Suy ra ${\hat{C}}_1+{\hat{D}}_1=\frac{1}{2}\left(\hat{C}+\hat{D}\right)$

${\hat{C}}_1+{\hat{D}}_1=\frac{1}{2}\left(\hat{C}+\hat{D}\right)=\frac{1}{2}\cdot 190°=95°$.

Áp dụng Định lí tổng ba góc của tam giác COD có: 

$\widehat{COD}=180°-\left({\hat{C}}_1+{\hat{D}}_1\right)=180°-95°=85°$.

Vậy $\widehat{COD}=85°$.

Ví dụ 2. Cho tứ giác ABCD có $\hat{A}:\hat{B}:\hat{C}:\hat{D}=6:5:4:3$. Tính các góc của tứ giác ABCD.

Hướng dẫn giải

Tứ giác ABCD có $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$.

Mặt khác $\hat{A}:\hat{B}:\hat{C}:\hat{D}=6:5:4:3$, theo tính chất dãy tỷ số bằng nhau ta có:

$\frac{\hat{\text{A}}}{6}+\frac{\hat{\text{B}}}{5}+\frac{\hat{\text{C}}}{4}+\frac{\hat{\text{D}}}{3}=\frac{\hat{\text{A}}+\hat{\text{B}}+\hat{\text{C}}+\hat{\text{D}}}{6+5+4+3}=\frac{360°}{18}=20°$.

Suy ra $\hat{A}=20°.6=120°$; $\hat{\text{B}}\text{= 20°. 5 = 100°}$;

$\hat{C}=20°.4=80°$; $\hat{D}=20°.3=60°$.

Vậy $\hat{A}=120°;\hat{B}=100°;\hat{C}=80°;\hat{D}=60°.$