Hãy lập các biểu thức tính một trong ba đại lượng s, v và t theo hai đại lượng còn lại.
Có phải tất cả các biểu thức đó đều là đa thức? Hãy giải thích.
Lời giải:
Ta lập được các biểu thức tính một trong ba đại lượng s, v và t theo hai đại lượng còn lại như sau: s = vt; v = ; t = .
Trong ba biểu thức trên, chỉ có biểu thức s = vt là đa thức; hai biểu thức còn lại không phải là đa thức, vì hai biểu thức v = và t = có chứa phép chia giữa các biến.
1. Phân thức đại số
Khám phá 1 trang 26 Toán 8 Tập 1: a) Viết biểu thức biểu thị các đại lượng sau đây:
• Chiều rộng của hình chữ nhật có chiều dài bằng a (m) và diện tích bằng 3 m2.
• Thời gian để một người thợ làm được x sản phẩm, biết rằng mỗi giờ người thợ đó làm được y sản phẩm.
• Năng suất trung bình của một mảnh ruộng gồm hai thửa, một thửa có diện tích a (ha) cho thu hoạch được m tấn lúa, thửa kia có diện tích b (ha) cho thu hoạch n tấn lúa.
b) Các biểu thức trên có đặc điểm nào giống nhau? Chúng có phải là đa thức không?
Lời giải:
a)
• Biểu thức biểu thị chiều rộng của hình chữ nhật có chiều dài bằng a (m) và diện tích bằng 3 m2 là: (m).
• Gọi t là thời gian để người thợ đó làm được x sản phẩm.
Vì thời gian làm việc và số sản phẩm làm được là hai đại lượng tỉ lệ thuận nên ta có:
= , suy ra t = (giờ)
Vậy biểu thức biểu thị thời gian để người thợ đó làm được x sản phẩm là: (giờ).
• Diện tích của mảnh ruộng là: a + b (ha).
Mảnh ruộng cho thu hoạch được số tấn lúa là: m + n (tấn lúa).
Biểu thức biểu thị năng suất trung bình của mảnh ruộng gồm hai thửa đó là: (tấn/ha).
b) Các biểu thức trên đều là biểu thức có dạng , trong đó A, B là những đa thức và B khác đa thức không.
Do đó các biểu thức này không phải là đa thức.
Khám phá 2 trang 27 Toán 8 Tập 1: Cho biểu thức
a) Tính giá trị của biểu thức tại x = 0.
b) Tại - , giá trị của biểu thức có xác định không? Tại sao?
Lời giải:
a) Tại x = 0, ta có: .
b) Tại ta có mẫu thức có giá trị là: .
Khi đó giá trị của biểu thức P không xác định.
Thực hành 1 trang 27 Toán 8 Tập 1: Tìm giá trị của phân thức:
a) tại x = –3, x = 1;
b) tại x = 3, y = –1.
Lời giải:
a) Xét phân thức
Điều kiện xác định của phân thức trên là x + 2 ≠ 0, hay x ≠ ‒2.
• Khi x = –3 (điều kiện xác định được thỏa mãn), ta có:
• Khi x = 1 (điều kiện xác định được thỏa mãn), ta có:
.
b) Xét phân thức
Điều kiện xác định của phân thức trên là x + y ≠ 0 (nghĩa là các giá trị của x và y thỏa mãn x + y ≠ 0).
Khi x = 3 và y = –1 thì x + y = 2 ≠ 0 nên điều kiện xác định được thỏa mãn.
Khi đó ta có: .
Thực hành 2 trang 27 Toán 8 Tập 1: Viết điều kiện xác định của mỗi phân thức:
a) ;
b) .
Lời giải:
a) Điều kiện xác định của phân thức là a + 4 ≠ 0 hay a ≠ ‒4.
b) Điều kiện xác định của phân thức là x – 2y ≠ 0 (nghĩa là tại các giá trị của x và y thỏa mãn x – 2y ≠ 0).
Lời giải:
• Khi x = 100, thay vào biểu thức C(x) ta được:
(nghìn đồng).
• Khi x = 1000, thay vào biểu thức C(x) ta được:
(nghìn đồng).
2. Hai phân thức bằng nhau
Khám phá 3 trang 28 Toán 8 Tập 1: Xét hai phân thức và
a) Tính giá trị của các phân thức trên khi x = 3, y = 2 và khi x = ‒1, y = 5.
Nêu nhận xét về giá trị của M và N khi cho x và y nhận những giá trị nào đó (y ≠ 0 và xy – y ≠ 0).
b) Nhân tử thức của phân thức này với mẫu thức của phân thức kia, rồi so sánh hai đa thức nhận được.
Lời giải:
a) • Khi x = 3 và y = 2 ta có: ;
• Khi x = ‒1 và y = 5 ta có: ;
.
Nhận xét: Giá trị của M và N bằng nhau khi cho x và y nhận những giá trị thỏa mãn y ≠ 0 và xy – y ≠ 0.
b) • Nhân tử thức của phân thức M với mẫu thức của phân thức N ta được:
x.(xy – y) = x2y – xy.
• Nhân tử thức của phân thức N với mẫu thức của phân thức M ta được:
(x2 – x).y = x2y – xy.
Ta thấy cả hai kết quả đều là đa thức x2y – xy nên hai đa thức nhận được bằng nhau.
Thực hành 3 trang 28 Toán 8 Tập 1: Mỗi cặp phân thức sau đây có bằng nhau không? Tại sao?
a) và ;
b) và
Lời giải:
a) Ta có: xy2.(x + 1) = x2y2 + xy2;
(xy + y).xy = x2y2 + xy2.
Do đó xy2.(x + 1) = (xy + y).xy.
Vậy = .
b) Ta có: (xy – y).y = xy2 – y2;
x.(xy – x) = x2y – x2.
Do đó (xy – y).y ≠ x.(xy – x)
Vậy hai phân thức và không bằng nhau.
3. Tính chất cơ bản của phân thức
Khám phá 4 trang 28 Toán 8 Tập 1: Xét các phân thức , ,
a) Các phân thức trên có bằng nhau không? Tại sao?
b) Có thể biến đổi như thế nào để chuyển Q thành P và R thành Q?
Lời giải:
a) • Xét hai phân thức và ta có:
x2y.y = x2y2;
xy2.x = x2y2.
Do đó x2y.y = xy2.x
Vậy = hay P = Q (1)
• Xét hai phân thức và ta có:
x.(xy + y2) = x2y + xy2;
y.(x2 + xy) = x2y + xy2.
Do đó x.(xy + y2) = y.(x2 + xy)
Vậy = , hay Q = R (2)
Từ (1) và (2) ta có P = Q = R.
Vậy các phân thức P, Q và Q bằng nhau.
b) • Ta nhân cả tử và mẫu của phân thức với cùng đơn thức xy khác đa thức không thì được: .
• Ta có:
Ta chia cả tử và mẫu của phân thức R cho cùng nhân tử chung là (x + y) thì được:
.
Giải Toán 8 trang 29 Tập 1
Thực hành 4 trang 29 Toán 8 Tập 1: Chứng tỏ hai phân thức và bằng nhau theo hai cách khác nhau
Lời giải:
Cách 1:
Xét hai phân thức và ta có:
(a2 – b2).ab = a3b – ab3;
(a2b + ab2)(a – b) = a3b – a2b2 + a2b2 – ab3 = a3b – ab3.
Do đó (a2 – b2).ab = (a2b + ab2)(a – b).
Vậy = .
Cách 2: Dùng tính chất cơ bản của phân thức
Ta có .
Vậy = .
Thực hành 5 trang 30 Toán 8 Tập 1: Rút gọn các phân thức sau:
a) ;
b) ;
c) .
Lời giải:
a) ;
b) ;
c) .
Bài tập
Bài 1 trang 30 Toán 8 Tập 1: Trong các biểu thức sau, biểu thức nào là phân thức?
; 2x2 – 5x + 3; .
Lời giải:
Trong các biểu thức trên, và 2x2 – 5x + 3 là phân thức.
Biểu thức không phải là phân thức, vì không phải là đa thức.
Bài 2 trang 30 Toán 8 Tập 1: Viết điều kiện xác định của các phân thức sau:
a) ;
b) ;
c) 3x2 – x + 7.
Lời giải:
a) Điều kiện xác định của phân thức là x – 6 ≠ 0, hay x ≠ 6.
b) Điều kiện xác định của phân thức là x + 3y ≠ 0 (nghĩa là tại các giá trị của x và y thỏa mãn x + 3y ≠ 0).
c) Phân thức 3x2 – x + 7 xác định với mọi giá trị x ∈ ℝ.
Bài 3 trang 30 Toán 8 Tập 1: Tìm giá trị của phân thức:
a) tại x = ‒ 4;
b) tại a = 4, b = ‒2.
Lời giải:
a) Xét phân thức
Điều kiện xác định của phân thức A là (x + 1)2 ≠ 0, hay x + 1 ≠ 0, do đó x ≠ –1.
Với điều kiện xác định x ≠ –1 thì .
Tại x = ‒ 4 (điều kiện xác định được thỏa mãn), ta có:
.
b) Xét phân thức .
Điều kiện xác định của phân thức B là a2 – b2 ≠ 0 (nghĩa là các giá trị của a và b thỏa mãn a2 – b2 ≠ 0).
Với điều kiện xác định trên thì .
Tại a = 4 và b = ‒2 thì a2 – b2 = 12 ≠ 0 nên điều kiện xác định được thỏa mãn.
Khi đó, .
Bài 4 trang 30 Toán 8 Tập 1: Mỗi cặp phân thức sau có bằng nhau không? Tại sao?
a) và ;
b) và .
Lời giải:
a) Xét hai phân thức và ta có:
3ac.2a2b = 6a3bc;
a3b.6c = 6a3bc.
Do đó 3ac.2a2b = a3b.6c
Vậy = .
b) Ta có: .
Vậy .
Bài 5 trang 30 Toán 8 Tập 1: Tìm đa thức thích hợp thay vào 
Lời giải:
a) Ta có
Vậy đa thức thay vào 
b) Ta có .
Vậy đa thức thay vào 
Bài 6 trang 30 Toán 8 Tập 1: Rút gọn các phân thức sau:
b) ;
c) ;
d) .
Lời giải:
a) ;
b) ;
c) ;
d) .
Video bài giảng Toán 8 Phân thức đại số - Chân trời sáng tạo


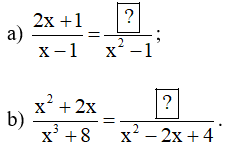
0 Comments:
Đăng nhận xét