Giải bài tập Toán lớp 8 Bài 6: Cộng, trừ phân thức

Giải Toán 8 trang 31 Tập 1

Khởi động trang 31 Toán 8 Tập 1: Tại một cuộc đua thuyền diễn ra trên một khúc sông từ A đến B dài 3 km. Mỗi đội thực hiện một vòng đua, xuất phát từ A đến B, rồi quay về A là đích. Một đội đua đạt tốc độ (x + 1) km/h khi xuôi dòng từ A đến B và đạt tốc độ (x – 1) km/h khi ngược dòng từ B về A. Thời gian thi của đội là bao nhiêu? Chiều về mất thời gian nhiều hơn chiều đi bao nhiêu giờ? Cần dùng phép tính nào để tìm các đại lượng đó?

Lời giải:

Thời gian đội đua xuôi dòng từ A đến B là: $\frac{3}{x+1}$ (giờ).

Thời gian đội đua ngược dòng từ B về A là: $\frac{3}{x-1}$ (giờ).

Thời gian thi của đội là: $\frac{3}{x+1}$ + $\frac{3}{x-1}$ (giờ).

Chiều về mất thời gian nhiều hơn chiều đi là: $\frac{3}{x-1}$ - $\frac{3}{x+1}$(giờ).

Như vậy ta cần dùng phép tính cộng để tìm thời gian thi của đội và dùng phép tính trừ để tìm thời gian chiều về nhiều hơn chiều đi.

1. Cộng, trừ hai phân thức cùng mẫu

Khám phá 1 trang 31 Toán 8 Tập 1: Một hình chữ nhật lớn được ghép bởi hai hình chữ nhật A và B lần lượt có diện tích là a cm2, b cm2 và có cùng chiều dài x cm (Hình 1)

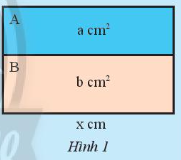
a) Tính chiều rộng của hình chữ nhật lớn theo hai cách khác nhau.

b) Chiều rộng của B lớn hơn chiều rộng của A bao nhiêu? Biết b > a.

Lời giải:

a) Cách 1:

Diện tích của hình chữ nhật lớn là: a + b (cm2).

Chiều rộng của hình chữ nhật lớn là: $\frac{a+b}{x}$ (cm).

Cách 2:

Chiều rộng của hình chữ nhật A là: $\frac{a}{x}$ (cm).

Chiều rộng của hình chữ nhật B là: $\frac{b}{x}$ (cm).

Chiều rộng của hình chữ nhật lớn là: $\frac{a}{x}$ + $\frac{b}{x}$ (cm).

b) Chiều rộng của hình chữ nhật B lớn hơn chiều rộng của hình chữ nhật A là:

$\frac{b}{x}$ - $\frac{a}{x}$ (cm).

Giải Toán 8 trang 32 Tập 1

Thực hành 1 trang 32 Toán 8 Tập 1: Thực hiện các phép cộng, trừ phân thức sau:

a) $\frac{x}{x+3}+\frac{2-x}{x+3}$;

b) $\frac{x^{2}y}{x-y}-\frac{x{y}^2}{x-y}$;

c) $\frac{2x}{2x-y}+\frac{y}{y-2x}$.

Lời giải:

a) $\frac{x}{x+3}+\frac{2-x}{x+3}=\frac{x+2-x}{x+3}=\frac{2}{x+3}$;

b) $\frac{x^{2}y}{x-y}-\frac{x{y}^2}{x-y}=\frac{x^{2}y-x{y}^2}{x-y}=\frac{xy\left(x-y\right)}{x-y}=xy$;

c) $\frac{2x}{2x-y}+\frac{y}{y-2x}=\frac{2x}{2x-y}+\frac{y}{-\left(2x-y\right)}$

$=\frac{2x}{2x-y}+\frac{-y}{2x-y}$                              

$=\frac{2x+\left(-y\right)}{2x-y}=\frac{2x-y}{2x-y}=1$        

2. Cộng, trừ hai phân thức khác mẫu

Khám phá 2 trang 32 Toán 8 Tập 1: Cho hai phân thức $A=\frac{a+b}{ab}$ và $B=\frac{a-b}{a^2}$

a) Tìm đa thức thích hợp thay vào mỗi  sau đây:

b) Sử dụng kết quả trên, tính A + B và A – B.

Lời giải:

a) Ta có: $\frac{a+b}{ab}=\frac{\left(a+b\right).a}{ab.a}=\frac{a^2+ab}{a^{2}b}$. Do đó đa thức thay vào  là: a2 + ab.

  $\frac{a-b}{a^2}=\frac{\left(a-b\right).b}{a^2.b}=\frac{ab-b^2}{a^{2}b}$ . Do đó đa thức thay vào  là: ab – b2.

b) $A+B=\frac{a+b}{ab}+\frac{a-b}{a^2}$

 $=\frac{a^2+ab}{a^{2}b}+\frac{ab-b^2}{a^{2}b}$             

  $=\frac{a^2+ab+ab-b^2}{a^{2}b}$            

  $=\frac{a^2+2ab-b^2}{a^{2}b}$            .

$A-B=\frac{a+b}{ab}-\frac{a-b}{a^2}$

$=\frac{a^2+ab}{a^{2}b}-\frac{ab-b^2}{a^{2}b}$          

$=\frac{a^2+ab-\left(ab-b^2\right)}{a^{2}b}$          

$=\frac{a^2+ab-ab+b^2}{a^{2}b}$          

$=\frac{a^2+b^2}{a^{2}b}$.

Giải Toán 8 trang 34 Tập 1

Thực hành 2 trang 34 Toán 8 Tập 1: Thực hiện các phép cộng, trừ phân thức sau:

a) $\frac{a}{a-3}-\frac{3}{a+3}$;

b) $\frac{1}{2x}+\frac{2}{x^2}$;

c) $\frac{4}{x^2-1}-\frac{2}{x^2+x}$.

Lời giải:

a) $\frac{a}{a-3}-\frac{3}{a+3}$

$=\frac{a\left(a+3\right)}{\left(a-3\right)\left(a+3\right)}-\frac{3\left(a-3\right)}{\left(a-3\right)\left(a+3\right)}$

$=\frac{a^2+3a-\left(3a-9\right)}{\left(a-3\right)\left(a+3\right)}$

$=\frac{a^2+3a-3a+9}{\left(a-3\right)\left(a+3\right)}$

$=\frac{a^2+9}{\left(a-3\right)\left(a+3\right)}$;

b) $\frac{1}{2x}+\frac{2}{x^2}=\frac{x}{2x^2}+\frac{4}{2x^2}=\frac{x+4}{2x^2}$;

c) $\frac{4}{x^2-1}-\frac{2}{x^2+x}$

$=\frac{4}{\left(x+1\right)\left(x-1\right)}-\frac{2}{x\left(x+1\right)}$

$=\frac{4x}{x\left(x+1\right)\left(x-1\right)}-\frac{2\left(x-1\right)}{x\left(x+1\right)\left(x-1\right)}$

$=\frac{4x-\left(2x-2\right)}{x\left(x+1\right)\left(x-1\right)}=\frac{4x-2x+2}{x\left(x+1\right)\left(x-1\right)}$

$=\frac{2x+2}{x\left(x+1\right)\left(x-1\right)}=\frac{2\left(x+1\right)}{x\left(x+1\right)\left(x-1\right)}=\frac{2}{x\left(x-1\right)}$.

Thực hành 3 trang 34 Toán 8 Tập 1: Thực hiện phép tính $\frac{x}{x+y}+\frac{2xy}{x^2-y^2}-\frac{y}{x+y}$

Lời giải:

$\frac{x}{x+y}+\frac{2xy}{x^2-y^2}-\frac{y}{x+y}$

$=\frac{x}{x+y}-\frac{y}{x+y}+\frac{2xy}{x^2-y^2}$

$=\frac{x-y}{x+y}+\frac{2xy}{\left(x+y\right)\left(x-y\right)}$

$=\frac{{\left(x-y\right)}^2}{\left(x+y\right)\left(x-y\right)}+\frac{2xy}{\left(x+y\right)\left(x-y\right)}$

$=\frac{x^2-2xy+y^2+2xy}{\left(x+y\right)\left(x-y\right)}$

$=\frac{x^2+y^2}{\left(x+y\right)\left(x-y\right)}$

Vận dụng trang 34 Toán 8 Tập 1: Viết biểu thức tính tổng thời gian đi và về, chênh lệch thời gian giữa đi và về của đội đua thuyền ở tình huống trong Hoạt động khởi động (trang 31). Tính giá trị của các đại lượng này khi v = 6 km/h

Lời giải:

Thời gian đội đua xuôi dòng từ A đến B là: $\frac{3}{x+1}$ (giờ).

Thời gian đội đua ngược dòng từ B về A là: $\frac{3}{x-1}$ (giờ).

Thời gian thi của đội là:

$\frac{3}{x+1}+\frac{3}{x-1}=\frac{3\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}+\frac{3\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}$

                    $=\frac{3x-3+3x+3}{\left(x+1\right)\left(x-1\right)}=\frac{6x}{\left(x+1\right)\left(x-1\right)}$ (giờ).

Chiều về mất thời gian nhiều hơn chiều đi là:

$\frac{3}{x-1}-\frac{3}{x+1}=\frac{3\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}-\frac{3\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}$

                    $=\frac{3x+3-\left(3x-3\right)}{\left(x+1\right)\left(x-1\right)}=\frac{3x+3-3x+3}{\left(x+1\right)\left(x-1\right)}=\frac{6}{\left(x+1\right)\left(x-1\right)}$ (giờ).

Bài tập

Giải Toán 8 trang 35 Tập 1

Bài 1 trang 35 Toán 8 Tập 1: Thực hiện các phép cộng, trừ phân thức sau:

a) $\frac{a-1}{a+1}+\frac{3-a}{a+1}$

b) $\frac{b}{a-b}+\frac{a}{b-a}$

c) $\frac{{\left(a+b\right)}^2}{ab}-\frac{{\left(a-b\right)}^2}{ab}$

Lời giải:

a) $\frac{a-1}{a+1}+\frac{3-a}{a+1}=\frac{a-1+3-a}{a+1}=\frac{2}{a+1}$

b) $\frac{b}{a-b}+\frac{a}{b-a}$

$=\frac{b}{a-b}+\frac{a}{-\left(a-b\right)}=\frac{b}{a-b}-\frac{a}{a-b}$

$=\frac{b-a}{a-b}=\frac{-\left(a-b\right)}{a-b}=-1$

c) $\frac{{\left(a+b\right)}^2}{ab}-\frac{{\left(a-b\right)}^2}{ab}$

$=\frac{{\left(a+b\right)}^2-{\left(a-b\right)}^2}{ab}$

$=\frac{\left(a+b+a-b\right).\left[\left(a+b\right)-\left(a-b\right)\right]}{ab}$

$=\frac{2a.\left(a+b-a+b\right)}{ab}$

$=\frac{2a.2b}{ab}=4$

Bài 2 trang 35 Toán 8 Tập 1: Thực hiện các phép cộng, trừ phân thức sau:

a) $\frac{1}{2a}+\frac{2}{3b}$

b) $\frac{x-1}{x+1}-\frac{x+1}{x-1}$

c) $\frac{x+y}{xy}-\frac{y+z}{yz}$

d) $\frac{2}{x-3}-\frac{12}{x^2-9}$

e) $\frac{1}{x-2}+\frac{2}{x^2-4x+4}$

Lời giải:

a) $\frac{1}{2a}+\frac{2}{3b}=\frac{3b}{2a.3b}+\frac{2.2a}{3b.2a}=\frac{3b+4a}{6ab}$

b) $\frac{x-1}{x+1}-\frac{x+1}{x-1}$

$=\frac{{\left(x-1\right)}^2}{\left(x+1\right)\left(x-1\right)}-\frac{{\left(x+1\right)}^2}{\left(x+1\right)\left(x-1\right)}$

$=\frac{x^2-2x+1-\left(x^2+2x+1\right)}{\left(x+1\right)\left(x-1\right)}$

$=\frac{x^2-2x+1-x^2-2x-1}{\left(x+1\right)\left(x-1\right)}$

$=\frac{-4x}{\left(x+1\right)\left(x-1\right)}$;

c) $\frac{x+y}{xy}-\frac{y+z}{yz}$

$=\frac{\left(x+y\right)z}{xyz}-\frac{\left(y+z\right)x}{xyz}$

$=\frac{xz+yz-\left(xy+xz\right)}{xyz}$

$=\frac{xz+yz-xy-xz}{xyz}$

$=\frac{yz-xy}{xyz}=\frac{y\left(z-x\right)}{xyz}=\frac{z-x}{xz}$

d) $\frac{2}{x-3}-\frac{12}{x^2-9}$

$=\frac{2}{x-3}-\frac{12}{\left(x-3\right)\left(x+3\right)}$

$=\frac{2\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}-\frac{12}{\left(x-3\right)\left(x+3\right)}$

$=\frac{2x+6-12}{\left(x-3\right)\left(x+3\right)}=\frac{2x-6}{\left(x-3\right)\left(x+3\right)}$

$=\frac{2\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{2}{x+3}$

e) $\frac{1}{x-2}+\frac{2}{x^2-4x+4}$

$=\frac{1}{x-2}+\frac{2}{{\left(x-2\right)}^2}$

$=\frac{x-2}{{\left(x-2\right)}^2}+\frac{2}{{\left(x-2\right)}^2}$

$=\frac{x-2+2}{{\left(x-2\right)}^2}=\frac{x}{{\left(x-2\right)}^2}$

Bài 3 trang 35 Toán 8 Tập 1: Thực hiện các phép tính sau:

a) $\frac{x+2}{x-1}-\frac{x-3}{x-1}+\frac{x-4}{1-x}$

b) $\frac{1}{x+5}-\frac{1}{x-5}+\frac{2x}{x^2-25}$

c) $x+\frac{2y^2}{x+y}-y$

Lời giải:

a) $\frac{x+2}{x-1}-\frac{x-3}{x-1}+\frac{x-4}{1-x}$

$=\frac{x+2-\left(x-3\right)}{x-1}+\frac{x-4}{-\left(x-1\right)}$

$=\frac{x+2-x+3}{x-1}-\frac{x-4}{x-1}$

$=\frac{5-\left(x-4\right)}{x-1}=\frac{5-x+4}{x-1}=\frac{9-x}{x-1}$

b) $\frac{1}{x+5}-\frac{1}{x-5}+\frac{2x}{x^2-25}$

$=\frac{1}{x+5}-\frac{1}{x-5}+\frac{2x}{\left(x+5\right)\left(x-5\right)}$

$=\frac{x-5}{\left(x+5\right)\left(x-5\right)}-\frac{x+5}{\left(x+5\right)\left(x-5\right)}+\frac{2x}{\left(x+5\right)\left(x-5\right)}$

$=\frac{x-5-\left(x+5\right)+2x}{\left(x+5\right)\left(x-5\right)}$

$=\frac{x-5-x-5+2x}{\left(x+5\right)\left(x-5\right)}$

$=\frac{2x-10}{\left(x+5\right)\left(x-5\right)}$

$=\frac{2\left(x-5\right)}{\left(x+5\right)\left(x-5\right)}=\frac{2}{x+5}$

c) $x+\frac{2y^2}{x+y}-y$

$=x-y+\frac{2y^2}{x+y}$

$=\frac{\left(x-y\right)\left(x+y\right)}{x+y}+\frac{2y^2}{x+y}$

$=\frac{x^2-y^2+2y^2}{x+y}=\frac{x^2+y^2}{x+y}$

Bài 4 trang 35 Toán 8 Tập 1: Cùng đi từ thành phố A đến thành phố B cách nhau 450 km, xe khách chạy với tốc độ x (km/h); xe tải chạy với tốc độ y (km/h) (x > y). Nếu xuất phát cùng lúc thì xe khách đến thành phố B sớm hơn xe tải bao nhiêu giờ?

Lời giải:

Thời gian xe khách đi từ thành phố A đến thành phố B là: $\frac{450}{x}$ (giờ).

Thời gian xe tải đi từ thành phố A đến thành phố B là: $\frac{450}{y}$ (giờ).

Vì x > y nên xe khách đến thành phố B sớm hơn xe tải hay xe tải đi mất thời gian nhiều hơn xe khách.

Do đó nếu xuất phát cùng lúc thì xe khách đến thành phố B sớm hơn xe tải số giờ là:

$\frac{450}{y}-\frac{450}{x}=\frac{450x}{xy}-\frac{450y}{xy}=\frac{450x-450y}{xy}$ (giờ).

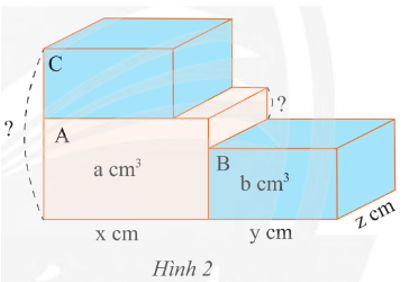
Bài 5 trang 35 Toán 8 Tập 1: Có ba hình hộp chữ nhật A, B, C có chiều dài, chiều rộng và thể tích được cho như Hình 2. Hình B và C có các kích thước giống nhau, hình A có cùng chiều rộng với B và C

a) Tính chiều cao của các hình hộp chữ nhật. Biểu thị chúng bằng các phân thức cùng mẫu số.

b) Tính tổng chiều cao của hình A và C, chênh lệch chiều cao của hình A và B.

Lời giải:

a) Diện tích đáy của hình hộp chữ nhật A là: xz (cm2).

Chiều cao của hình hộp chữ nhật A là: $\frac{a}{xz}$ (cm).

Diện tích đáy của hình hộ chữ nhật B là: yz (cm2).

Chiều cao của hình hộp chữ nhật B là: $\frac{b}{yz}$ (cm).

Do hình B và C có các kích thước giống nhau nên chiều cao của hình hộp chữ nhật C là $\frac{b}{yz}$ (cm).

Biểu thị các phân thức $\frac{a}{xz}$ và $\frac{b}{yz}$ bằng các phân thức cùng mẫu số như sau: $\frac{a}{xz}=\frac{ay}{xyz};\frac{b}{yz}=\frac{bx}{xyz}$.

Vậy chiều cao của hình hộp chữ nhật A, B và C lần lượt là $\frac{ay}{xyz}$ (cm); $\frac{bx}{xyz}$ (cm) và $\frac{bx}{xyz}$ (cm).

b) Tổng chiều cao của hình A và C là: $\frac{ay}{xyz}+\frac{bx}{xyz}=\frac{ay+bx}{xyz}$ (cm).

Chênh lệch chiều cao của hình A và B là: $\frac{ay}{xyz}-\frac{bx}{xyz}=\frac{ay-bx}{xyz}$ (cm).

Video bài giảng Toán 8 Bài 6: Cộng, trừ phân thức - Chân trời sáng tạo