Diện tích xung quanh và thể tích của hình chóp tứ giác đều

 1. Công thức 

a) Diện tích xung quanh của hình chóp tứ giác đều

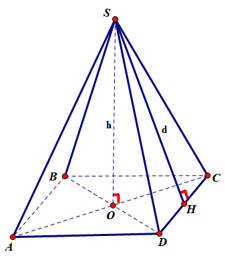
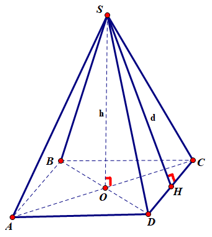
Diện tích xung quanh của hình chóp tứ giác đều bằng tích của nửa chu vi đáy với trung đoạn.

Sxq = p.d

Trong đó: p: nửa chu vi đáy;

      d: trung đoạn.

b) Thể tích của hình chóp tứ giác đều

Thể tích của hình chóp tứ giác đều bằng $\frac{1}{3}$ tích của diện tích mặt đáy với chiều cao của nó.

$V=\frac{1}{3}.S.h$

Trong đó: S: diện tích đáy,

                 h: chiều cao của hình chóp.

2. Ví dụ minh hoạ

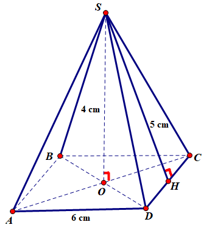
Ví dụ 1. Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều S.ABCD, biết độ dài cạnh đáy bằng 6 cm, chiều cao bằng 4 cm, trung đoạn bằng 5 cm.

Hướng dẫn giải

Nửa chu vi đáy ABCD là: (4 . 6) : 2 = 12 (cm)

Diện tích xung quanh của hình chóp tứ giác đều S.ABCD là:

Sxq  = p.d = 12. 5 = 60 (cm2)

Diện tích đáy ABCD là: S = 62 = 36 (cm2)

Thể tích của hình chóp tứ giác đều S.ABCD là:

$V=\frac{1}{3}S.h=\frac{1}{3}\cdot 36\cdot 4=48\left(c{m}^3\right)$

Vậy diện tích xung quanh và thể tích của hình chóp tứ giác đều S.ABCD lần lượt là 60 cm2 và 48 cm3.

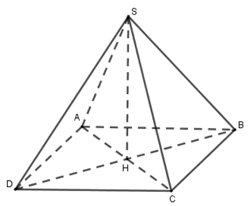
Ví dụ 2. Một hình chóp tứ giác đều có thể tích bằng 200cm3, chiều cao bằng 12cm. Tính độ dài cạnh bên.

Hướng dẫn giải

Xét hình chóp tứ giác đều S.ABCD có V = 200cm3, đường cao SH = 12cm.

Ta có: $V=\frac{1}{3}S.h$

Suy ra $S=\frac{3V}{SH}=\frac{3.200}{12}=50\left(c{m}^2\right)$

Do đó BC2 = 50

Tam giác BHC vuông cân nên HB2 + HC2 = BC2(định lý Pythagore)

Hay 2HC2 = BC2 hay 2HC2 = 50

Suy ra HC2 = 25

SC2 = SH2 + HC2 = 122 + 252 = 169 = 132

Vậy SC = 13cm.

Vậy độ dài cạnh bên là 13cm.