Công thức Trường hợp bằng nhau thứ nhất của tam giác cạnh cạnh cạnh

 1. Công thức

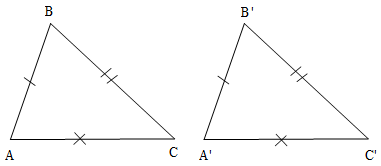
Cho hai tam giác ABC và A'B'C' có AB = A'B', AC = A'C', BC = B'C'.

Khi đó: ∆ABC = ∆A'B'C' (c.c.c)

2. Ví dụ minh họa:

Ví dụ 1. Cho hình chữ nhật ABCD như hình vẽ. Chứng minh ∆ABC = ∆CDA.

Hướng dẫn giải:

Xét ∆ABC và ∆CDA ta có:

AB = CD (tính chất hình chữ nhật)

BC = DA (tính chất hình chữ nhật)

Cạnh AC chung

Vậy ∆ABC = ∆CDA (c.c.c)

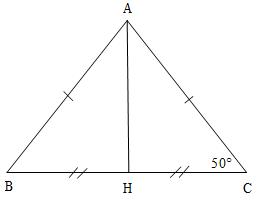
Ví dụ 2. Cho tam giác ABC như hình vẽ. Biết AB = AC và H là trung điểm đoạn BC.

a) Chứng minh ∆ABH = ∆ACH

b) Tính số đo góc BAH

Hướng dẫn giải:

GT	∆ABC, AB = AC H là trung điểm đoạn BC
KL	a) ∆ABH = ∆ACH. b) $\widehat{BAH}=?$

a) Xét ∆ABH và ∆ACHta có:

AB = AC (giả thiết)

AH là cạnh chung

BH = CH (vì H là trung điểm BC)

Vậy ∆ABH = ∆ACH (c.c.c)

b) Vì ∆AHC vuông tại H nên $\widehat{CAH}+\widehat{ACH}=90°$ (hai góc phụ nhau)

Suy ra $\widehat{\text{CAH}}\text{=90°}-\widehat{\text{ACH}}\text{=90°}-\text{50°=40°}$

Lại có $\widehat{CAH}=\widehat{BAH}$ (vì ∆ABH = ∆ACH)

Vậy $\widehat{BAH}=40°$.

3. Bài tập tự luyện

Bài 1. Cho đoạn thẳng AB dài 4 cm. Vẽ đường tròn tâm A bán kính 2 cm và đường tròn tâm B bán kính 3 cm, chúng cắt nhau ở C và D. Chứng minh rằng:

a) ∆ACB = ∆ADB;

b) AB là tia phân giác góc CAD.

Bài 2. Cho tam giác MNP có NP = 2 cm, MN = MP = 3 cm. Gọi E là trung điểm của cạnh NP.

a) Chứng minh rằng ∆NME = ∆PME;

b) Tính số đo góc $\widehat{NME}$, biết $\widehat{NMP}=24°$.

Bài 3. Cho tam giác ABC có AB < AC. Gọi K $\in$ AC sao cho AB = CI. Gọi I là một điểm nằm trong tam giác sao cho IA = IC, IB = IK.

a) Chứng minh ∆AIB = ∆CIK;

b) Tính số đo góc ABI. Biết $\widehat{IKC}=46°$.

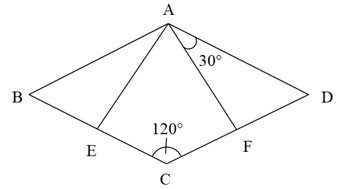
Bài 4. Cho hình thoi ABCD như hình vẽ. Biết E, F lần lượt là trung điểm các cạnh BC, DC.

a) Chứng minh ∆ABE = ∆ADF;

b) Tính số đo góc EAF.

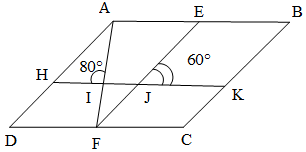
Bài 5. Cho hình bình hành ABCD như hình vẽ.

a) Chứng minh ∆ADF = ∆FEA;

b) Tính số đo góc IEJ.