1. Công thức
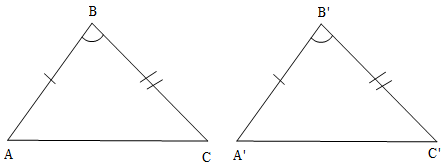
Cho hai tam giác ABC và A'B'C' có AB = A'B', , BC = B'C'.
Khi đó: ∆ABC = ∆A'B'C' (c.g.c).
2. Ví dụ minh họa:
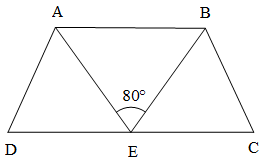
Ví dụ 1. Cho hình thang cân ABCD như hình vẽ. Biết E là trung điểm của đoạn CD.
a) Chứng minh ∆ADE = ∆BCE.
b) Tính .
Hướng dẫn giải:
GT | ABCD là hình thang cân E là trung điểm của đoạn CD |
KL | a) ∆ADE = ∆BCE b) |
a) Xét ∆ADE và ∆BCE, ta có:
AD = BC (tính chất hình thang)
(tính chất hình thang)
DE = EC (E là trung điểm đoạn CD)
Vậy ∆ADE = ∆BCE (c.g.c)
b) Ta có: (1)
Từ câu a: ∆ADE = ∆BCE nên suy ra (hai góc tương ứng) (2)
Từ (1) và (2) suy ra
Do đó
Áp dụng định lý tổng ba góc của tam giác vào ∆ADE, ta có:
Suy ra
Vậy .
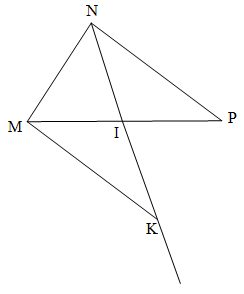
Ví dụ 2. Cho tam giác MNP. Gọi I là trung điểm của MP. Trên tia đối của tia IN lấy điểm K sao cho IN = IK. Chứng minh rằng:
a) MK = PN;
b) MK // PN.
Hướng dẫn giải:
GT | ∆MNP, I là trung điểm của đoạn MP IN = IK |
KL | a) MK = PN b) MK // PN |
a) Xét ∆MIK và ∆PIN, có:
IN = IK (giả thiết)
(hai góc đối đỉnh)
IM = IP (I là trung điểm của MP)
Do đó ∆MIK = ∆PIN (c.g.c).
Suy ra MK = PN (hai cạnh tương ứng).
b) Từ câu a: ∆MIK = ∆PIN suy ra (hai góc tương ứng)
Mà hai góc và nằm ở vị trí so le trong nên suy ra MK // PN.
3. Bài tập tự luyện
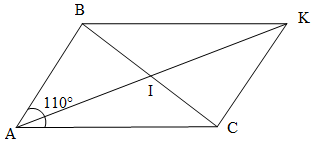
Bài 1. Cho hình vẽ bên dưới. Biết rằng I trung điểm BC và IK = IA
a) Chứng minh ∆ABI = ∆KCI.
b) Tính số đo góc ABK.
Bài 2. Cho tam giác ABC có I là trung điểm của BC. Trên tia đối IA lấy điểm K sao cho IK = IA. Về phía ngoài của tam giác ABC vẽ các đoạn thẳng AD vuông góc và bằng AB, AE vuông góc và bằng AC.
a) Chứng minh ∆ABK = ∆DAE.
b) Chứng minh IA ⊥ DE.
Bài 3. Cho tam giác ABC, kẻ AH vuông góc với BC (H ∈ BC). Trên tia đối của tia HA, lấy điểm K sao cho HK = HA. Nối KB, KC. Tìm các cặp tam giác bằng nhau.
Bài 4. Cho góc xOy. Trên cạnh Ox lấy các điểm M và N, trên cạnh Oy lấy các điểm P và Q sao cho OM = OP, ON = OQ.
a) Chứng minh rằng MQ = NP.
b) Chứng minh MQ // NP.
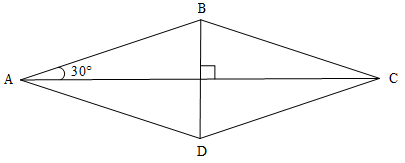
Bài 5. Cho hình thoi ABCD như hình vẽ.
a) Chứng minh ∆ABO = ∆CDO
b) Tính số đo góc CDA.

0 Comments:
Đăng nhận xét