Công thức Trường hợp bằng nhau thứ ba của tam giác góc cạnh góc

 1. Công thức

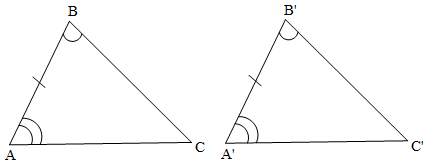
Cho hai tam giác ABC và A'B'C' có $\widehat{CAB}=\widehat{C\text{'}A\text{'}B\text{'}}$ , AB = A'B'.

Khi đó: ∆ABC = ∆A'B'C' (g.c.g).

2. Ví dụ minh họa:

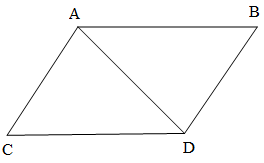
Ví dụ 1. Cho hình bình hành ABCD như hình vẽ.

a) Chứng minh $\widehat{ADC}=\widehat{DAB}$;

b) Chứng minh ∆CAD = ∆BDA.

Hướng dẫn giải:

GT	ABCD là hình bình hành
KL	a) $\widehat{ADC}=\widehat{DAB}$ b) ∆CAD = ∆BDA

a) Ta cóABCD là hình bình hành nên AB // CD

Mà $\widehat{ADC}$ và $\widehat{DAB}$ở vị trí so le trong

Do đó $\widehat{ADC}=\widehat{DAB}$ (đpcm)

b) Xét ∆CAD và ∆BDAta có:

$\widehat{ADC}=\widehat{DAB}$ (cmt)

AD cạnh chung

$\widehat{CAD}=\widehat{BDA}$ (hai góc so le trong)

Vậy ∆CAD = ∆BDA (g.c.g)

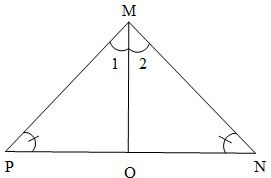
Ví dụ 2. Cho tam giác MNP có $\hat{N}=\hat{P}$, PQ = 3 cm. Tia phân giác góc M cắt NP tại Q. Chứng minh rằng:

a) ∆MQN = ∆MQP;

b) MN = MP.

c) Tính độ dài NQ.

Hướng dẫn giải:

GT	∆MNP, $\hat{N}=\hat{P}$ MQ là tia phân giác $\widehat{NMP}$ (Q $\in$ NP)
KL	a) ∆MQN = ∆MQP b) MN = MP c) NQ = ?

a) Áp dụng định lý tổng ba góc của một tam giác, ta có:

${\hat{M}}_1+\hat{P}+\widehat{\text{MQN}}\text{=}{\hat{M}}_2+\hat{N}+\widehat{\text{MQP}}={180}^o$.

Mặt khác: $\hat{\text{N}}\text{=}\hat{\text{P}}$ (giả thiết);

${\hat{\text{M}}}_{\text{1}}\text{=}{\hat{\text{M}}}_{\text{2}}$ (vì MQ là tia phân giác $\widehat{NMP}$ )

Do đó $\widehat{\text{MQN}}\text{=}\widehat{\text{MQP}}$.

Xét ∆MQN và ∆MQPta có:

${\hat{\text{M}}}_{\text{1}}\text{=}{\hat{\text{M}}}_{\text{2}}$ (vì MQ là tia phân giác $\widehat{NMP}$ )

MQ là cạnh chung

$\widehat{\text{MQN}}\text{=}\widehat{\text{MQP}}$ (cmt)

Vậy ∆MQN = ∆MQP (g.c.g)

b) Từ câu a: ∆MQN = ∆MQP

Suy ra MN = MP (hai cạnh tương ứng).

c) Từ câu a: ∆MQN = ∆MQP

Suy ra PQ = NQ (hai cạnh tương ứng)

Vậy NQ = 3 cm.

3. Bài tập tự luyện

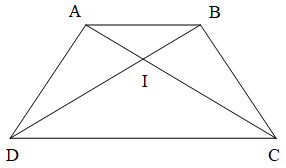
Bài 1. Cho hình thang ABCD cân như hình vẽ. Chứng minh rằng:

a) ∆ABD = ∆BAC;

b) ∆AID = ∆BIC;

c) $\widehat{\text{IDC}}\text{=}\widehat{\text{ICD}}$.

Bài 2. Cho tam giác ABC, có AK là tia phân giác góc A (K $\in$ BC), BH là tia phân giác góc B (H $\in$ AC). Gọi I là giao điểm của AK và BH. Chứng minh rằng: ∆BAH = ∆BKH. Biết rằng AB = BK.

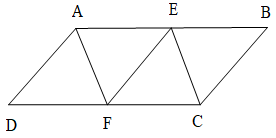
Bài 3. Cho hình bình hành ABCD có AB = 8 cm(như hình vẽ). Cho E , F lần lượt là trung điểm của đoạn AB và DC. Chứng minh rằng:

a) ∆DAF = ∆BCE;

b) ∆AFE = ∆CEF.

c) Tính độ dài DF.

Bài 4. Cho đoạn thẳng MP và NQ cắt nhau tại điểm I so cho IM = IP, IN = IQ. Chứng minh rằng:

a) MN // PQ;

b) ∆NMP = ∆QPN;

c) $\widehat{\text{QMP}}\text{=}\widehat{\text{NPM}}$.

Bài 5. Cho tam giác ABC có $\widehat{ABC}={45}^o$ . Đường thẳng qua A và song song với BC cắt đường thẳng qua C và song song với AB tại D.

a) Chứng minh rằng: ∆ABC = ∆CDA.

b) Gọi M và N lần lượt là trung điểm của AD và BC. Chứng minh rằng: MN và AC cắt nhau tại trung điểm của mỗi đường thẳng.

c) Tính $\widehat{MNC}$ .