Công thức Các trường hợp bằng nhau của tam giác vuông

 1. Công thức

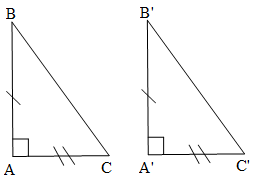
Trường hợp 1:Cho ∆ABC vuông tại A và ∆A'B'C' vuông tại A' có AB = A'B', AC = A'C'.

Khi đó: ∆ABC = ∆A'B'C' (hai cạnh góc vuông).

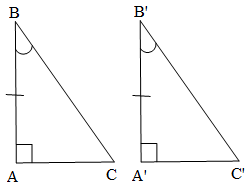
Trường hợp 2:Cho ∆ABC vuông tại A và ∆A'B'C' vuông tại A' có AB = A'B', $\widehat{\text{ABC}}\text{=}\widehat{\text{A'B'C'}}$ .

Khi đó: ∆ABC = ∆A'B'C'(cạnh góc vuông – góc nhọn kề).

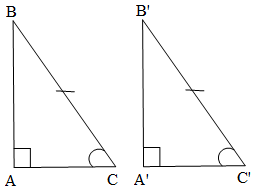
Trường hợp 3:Cho ∆ABC vuông tại A và ∆A'B'C' vuông tại A' có BC = B'C', $\widehat{\text{ACB}}\text{=}\widehat{\text{A'C'B'}}$ .

Khi đó: ∆ABC = ∆A'B'C' (cạnh huyền – góc nhọn).

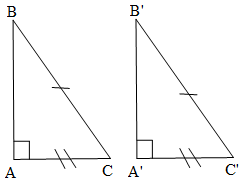
Trường hợp 4:Cho ∆ABC vuông tại A và ∆A'B'C' vuông tại A' có BC = B'C', AC = A'C'.

Khi đó: ∆ABC = ∆A'B'C' (cạnh huyền – cạnh góc vuông).

2. Ví dụ minh họa:

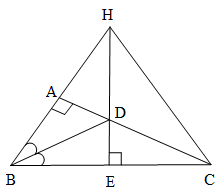
Ví dụ 1. Cho tam giác ABC vuông tại A có $\widehat{\text{ABC}}={60}^o$. Kẻ tia phân giác của $\widehat{\text{ABC}}$cắt AC tại D. Kẻ DE vuông góc với BC tại E. Hai đường thẳng BA và ED cắt nhau tại H. Chứng minh rằng:

a) ∆ABD = ∆EBD

b) ∆ADH = ∆EDC

c) ∆AHC = ∆ECH

Hướng dẫn giải:

GT	∆ABC vuông tại A có AB < AC DE ^BC tại E BA và ED cắt nhau tại H Tia phân giác của $\widehat{\text{ABC}}$cắt AC tạiD
KL	a) ∆ABD = ∆EBD b) ∆ADH = ∆EDC c) ∆AHC = ∆ECH

a) Xét ∆ABD và ∆EBD có:

$\widehat{\text{BAD}}\text{=}\widehat{\text{BED}}\text{=90°}$

Cạnh BD chung

$\widehat{\text{ABD}}\text{=}\widehat{\text{DEB}}$ (vì BD là tia phân giác )

Do đó ∆ABD = ∆EBD (cạnh huyền – góc nhọn)

b) Theo câu a: ∆ABD = ∆EBD (cmt)

Suy ra AD = ED (hai cạnh tương ứng)

Xét ∆ADH và ∆EDC có:

$\widehat{\text{DAH}}\text{=}\widehat{\text{DEC}}\text{=90°}$

AD = ED (cmt)

$\widehat{\text{ADH}}\text{=}\widehat{\text{EDC}}$ (hai góc đối đỉnh)

Do đó ∆ADH = ∆EDC (cạnh góc vuông – góc nhọn kề)

c) Từ câu b: ∆ADH = ∆EDC (cmt)

Suy ra AH = EC (hai cạnh tương ứng)

Xét ∆AHC và ∆ECH có:

$\widehat{\text{CAH}}\text{=}\widehat{\text{HEC}}\text{=90°}$

AH = EC (cmt)

Cạnh HC chung

Do đó ∆AHC = ∆ECH (cạnh huyền – cạnh góc vuông)

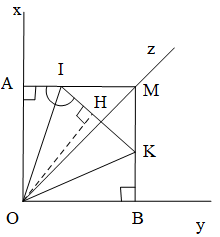
Ví dụ 2. Cho góc vuông xOy và tia phân giác Oz. Từ một điểm M trên tia Oz ta hạ MA vuông góc với Ox. MB vuông góc với Oy.

a) Chứng minh OA = OB.

b) Lấy điểm I trên đoạn thẳng AM. Nối I với O. Từ I kẻ một tia tạo với IO một góc bằng góc AIO. Tia này cắt đoạn thẳng MB ở K. Nối O với K. Tính số đo góc IOK.

Hướng dẫn giải:

GT	$\widehat{xOy}$ = 90o MA^ Ox MB^ Oy Oz là tia phân giác $\widehat{xOy}$ .
KL	OA = OB $\widehat{\text{IOK}}\text{=?}$

a) Vì MA⊥ Ox nên $\widehat{\text{MAO}}\text{=90°}$ ;

Vì MB⊥ Oy nên $\widehat{\text{MBO}}\text{=90°}$ .

Do đó $\widehat{\text{MAO}}\text{=}\widehat{\text{MBO}}\text{=90°}$

Xét ∆MAO và ∆MBO có:

$\widehat{\text{MAO}}\text{=}\widehat{\text{MBO}}\text{=90°}$ (cmt)

Cạnh MO chung

$\widehat{\text{MOA}}\text{=}\widehat{\text{MOB}}$ (vì Oz là tia phân giác $\widehat{xOy}$ )

Do đó ∆MAO = ∆MBO (cạnh huyền – góc nhọn)

Suy ra OA = OB (hai cạnh tương ứng)

b) Kẻ OH $\text{⊥}$ IK (H $\in$ IK).

Xét ∆OAI và ∆OHI có:

$\widehat{\text{OAI}}\text{=}\widehat{\text{OHI}}\text{=90°}$

Cạnh OI chung

$\widehat{\text{AIO}}\text{=}\widehat{\text{HIO}}$ (giả thiết)

Do đó ∆OAI = ∆OHI (cạnh huyền – góc nhọn)

Suy ra OA = OH và $\widehat{\text{AOI}}\text{=}\widehat{\text{IOH}}$ (1)

Xét hai tam giác vuông OHK và OBK có:

Cạnh OK chung

OH = OB (= OA)

Vậy ∆OHK = ∆OBK (cạnh huyền – cạnh góc vuông)

Suy ra $\widehat{\text{HOK}}\text{=}\widehat{\text{BOK}}$ (2)

Từ (1) và (2) suy ra $\widehat{\text{IOK}}\text{=}\frac{\text{1}}{\text{2}}\widehat{\text{xOy}}\text{=}\frac{\text{1}}{\text{2}}\text{.90°=45°}$

3. Bài tập tự luyện

Bài 1. Cho tam giác đều ABC. Trên nửa mặt phẳng không chứa C có bờ là đường thẳng AB ta kẻ đoạn thẳng BM vuông góc với BA và BM = BA, trên nửa mặt phẳng không chứa B có bờ là đường thẳng AC ta kẻ đoạn thẳng CN vuông góc với CA và CN = CA. Nối M với N. Chứng minh rằng:

a) ∆MHB = ∆NKC

b) MN // BC

Bài 2. Cho ∆ABC và ∆A’B’C’. Trong ∆ABC kẻ BH ⊥ AC. Tia phân giác góc B cắt AC tại D. Trong ∆A’B’C’ kẻ B’H’ ⊥ A’C’. Tia phân giác góc B’ cắt A’C’ ở D’. Biết rằng $\hat{\text{B}}\text{=}\widehat{\text{B'}}$, BH = B’H’, BD = B’D’. Chứng minh rằng:

a) ∆BHD = ∆B’H’D’;

b) ∆ABC = ∆A’B’C’.

Bài 3. Cho tam giác ABC vuông tại A (AB < AC) và các điểm M thuộc cạnh AC, H thuộc cạnh Bc sao cho MH vuông góc với BC và MH = HB. Chứng minh rằng:

a) ∆HKM = ∆HIB;

b) AH là tia phân giác của góc A.

Bài 4. Cho tam giác ABC vuông tại A (AB > AC). Tia phân gaics của góc B cắt AC ở D. Kẻ DH vuông góc với BC. Trên tia AC lấy điểm E sao cho AE = AB. Đường thẳng vuông góc với AE tại E cắt tia DH ở K. Chứng minh rằng:

a) BA = BH;

b) ∆HBK = ∆IBK;

c) $\widehat{\text{DBK}}\text{=90°}$.

Bài 5.Cho tam giác ABC có $\hat{A}$ = 35o. Đường thẳng AH vuông góc với BC tại H. Trên đường vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH = BD.

a) Chứng minh ΔAHB = ΔDBH.

b) Chứng minh AB // HD.

c) Gọi O là giao điểm của AD và BC. Chứng minh O là trung điểm của BH.