Công thức Tam giác cân, đường trung trực

 1. Công thức

a) Tam giác cân

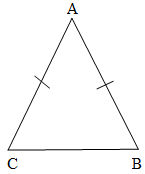
Tam giác cân là tam giác có hai cạnh bằng nhau.

• Cho ∆ABC cân tại A khi và chỉ khi AB = AC.

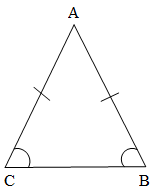
Tính chất: Trong một tam giác cân, hai góc ở đáy bằng nhau. Ngược lại, một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

• Cho ∆ABC cân tại A khi và chỉ khi $\hat{B}=\hat{C}$.

b) Đường trung trực của một đoạn thẳng

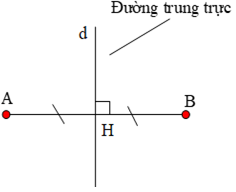
Định nghĩa:Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

• Cho d là trung trực của AB khi và chỉ khi $\left(\begin{array}{c}d\perp AB(\text{H}\in d)\\ HA=HB\end{array}\right)$

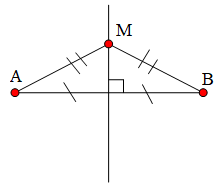
Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai nút của đoạn thẳng đó.

• Cho M thuộc đường trung trực của AB khi và chỉ khi MA = MB.

2. Ví dụ minh họa:

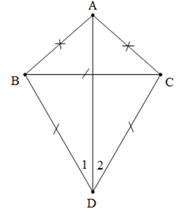
Ví dụ 1.Cho tam giác ABC cân tại A và tam giác đều BCD (D và A nằm khác phía đối với BC). Tính số đo góc BDA.

Giải:

GT	∆ABC, AB = AC ∆BCD, BC = BD = CD (D và A nằm khác phía đối với BC)
KL	$\widehat{BDA}=?$

Xét ∆ABD và ∆ACD có:

AB = AC (∆ABC cân)

BD = CD (∆BCD đều)

Cạnh AD chung

Do đó ∆ABD = ∆ACD (c.c.c)

Suy ra ${\hat{D}}_1={\hat{D}}_2$ (hai góc tương ứng)

Mặt khác, ∆BCD đều nên $\widehat{BDC}={60}^o={\hat{D}}_1+{\hat{D}}_2$

Suy ra ${\hat{D}}_1={\hat{D}}_2={30}^o$ .

Vậy $\widehat{BDA}={30}^o$

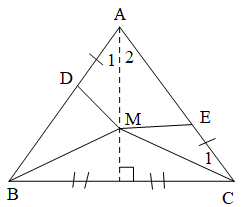
Ví dụ 2. Cho tam giác ABC cân tại A. Hai đường trung trực của các cạnh AB và BC cắt nhau tại M. Trên cạnh AB lấy một điểm D và trên cạnh AC lấy một điểm E sao cho AD = CE. Chứng minh rằng: MD = ME.

Hướng dẫn giải:

GT	∆ABC cân tại A M là giao hai đường trung trực của AB và BC AD = CE (D Î AB, E Î AC)
KL	MD = ME.

Vì ∆ABC cân tại A nên đường trung trực của cạnh BC đi qua đỉnh A chia góc tại đỉnh A ra làm hai góc bằng nhau ${\hat{\text{A}}}_{\text{1}}\text{=}{\hat{\text{A}}}_{\text{2}}$ (1)

Mặt khác M là giao của ba đường trung trục nên ta có: MA = MB = MC.

Vì MA = MC (cmt) nên ∆MAC cân tại M nên ${\hat{\text{A}}}_{\text{2}}\text{=}{\hat{\text{C}}}_{\text{1}}$ (2)

Từ (1) và (2) suy ra ${\hat{\text{A}}}_{\text{1}}\text{=}{\hat{\text{C}}}_{\text{1}}$

Xét ∆ADM và ∆CEM có:

AD = CE (giả thiết)

${\hat{\text{A}}}_{\text{1}}\text{=}{\hat{\text{C}}}_{\text{1}}$ (cmt)

MA = MC (cmt)

Do đó ∆ADM = ∆CEM (c.g.c)

Suy ra MD = ME (hai cạnh tương ứng)

3. Bài tập tự luyện

Bài 1. Cho tam giác ABC với phân giác trong AD. Từ một đỉnh P thuộc đoạn DC, kẻ một đường thẳng song song với AD, cắt các đường thẳng AB, AC lần lượt tại M và N. Chứng minh rằng: Đường trung trực của đoạn MN đi qua điểm A.

Bài 2. Cho tam giác ABC có AB < AC. Trên cạnh AC lấy điểm D sao cho CD = AB. Hai đường trung trực của BD và AC cắt nhau tại E. Chứng minh rằng:

a) ∆AEB = ∆CED

b) Tam giác AEC cân

c) AE là tia phân giác trong tại đỉnh A của tam giác ABC.

Bài 3. Cho góc nhọn xOy và một điểm M nằm trong góc ấy. Từ M kẻ các đường vuông góc MA, MB lần lượt xuống Ox và Oy. Gọi C là trung điểm của đoạn thẳng OM, P là trung điểm của đoạn thẳng AB. Chứng minh rằng: CP là đường trung trực của tam giác ABC.

Bài 4. Cho tam giác ABC vuông tại A có $\hat{\text{C}}\text{=30°}$. Trên cạnh BC lấy điểm M sao cho BM = BA. Chứng minh rằng:

a) Tam giác AMB cân.

b) $\text{AM=}\frac{\text{BC}}{\text{2}}$.

Bài 5. Cho tam giác ABC không vuông. Các đường trung trực của AB và AC cắt nhau tại O, cắt đường thẳng BC theo thứ tự M và N. Chứng minh rằng:

a) ∆AOM = ∆BOM.

b) Tam giác BOC cân.

c) Tia AO là tia phân giác của góc MAN.