Công thức Hai tam giác bằng nhau

 1. Công thức

Cho hai tam giác ABC và A'B'C' có $\left(\begin{array}{c}AB=A\text{'}B\text{'},AC=A\text{'}C\text{'},BC=B\text{'}C\text{'}\\ \hat{A}=\widehat{A\text{'}},\hat{B}=\widehat{B\text{'}},\hat{C}=\widehat{C\text{'}}\end{array}\right)$

Khi đó: ∆ABC = ∆A'B'C'.

2. Ví dụ minh họa:

Ví dụ 1. Cho ∆ABC = ∆MNP. Biết rằng AC = 3cm, $\widehat{BAC}=50°$, $\widehat{ACB}=60°$. Tính:

a) Độ dài cạnh MP.

b) Số đo góc MNP.

Hướng dẫn giải:

a) Theo đề bài, ∆ABC = ∆MNP (1)

Suy ra MP = AC = 3 cm (cặp cạnh tương ứng)

Vậy độ dài cạnh MP = 3cm.

b) Từ (1) suy ra $\widehat{ABC}=\widehat{MNP}$(cặp góc tương ứng)

Lại có $\widehat{ABC}+\widehat{BCA}+\widehat{CAB}=180°$ (tổng ba góc trong tam giác)

Suy ra $\widehat{ABC}=180°-\widehat{BCA}-\widehat{CAB}=180°-60°-50°=70°$

Do đó $\widehat{MNP}=\widehat{ABC}=70°$ .

Vậy $\widehat{MNP}=70°$.

Ví dụ 2. Cho ∆ABC = ∆DEF. Biết AB = 5 cm, DF = 6 cm, EF = 3 cm. Tính:

a) Tính số đo đoạn thẳng BC.

b) Tính chu vi tam giác ABC.

Hướng dẫn giải:

a) Theo đề bài, ∆ABC = ∆DEF (1)

Suy ra BC = EF = 3 cm (hai cạnh tương ứng)

Vậy BC = 3 cm.

b) Từ (1) ta suy ra AC = DF = 6 cm (hai cạnh tương ứng)

Chu vi tam giác ABC bằng:

AB + BC + AC = 5 + 3 + 6 = 14 (cm)

Vậy chu vi tam giác ABC bằng 14 cm.

3. Bài tập tự luyện

Bài 1. Cho hai tam giác ABC và DEF có AB = DE, BC = EF, AC = DF, $\hat{A}=\hat{D}$, $\hat{\text{C}}\text{=}\hat{\text{F}}$. Chứng minh rằng:

a) $\hat{\text{B}}\text{=}\hat{\text{E}};$

b) ∆ABC = ∆DEF.

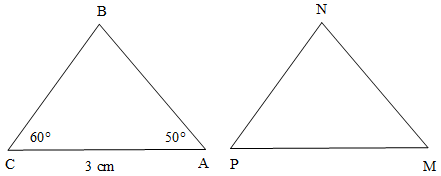
Bài 2. Cho ∆MNP = ∆DEF. Biết rằng MN = 8 cm, $\widehat{DEF}=90°$. Tính:

a) Độ dài cạnh DE.

b) $\widehat{NPM}+\widehat{PMN}=?$

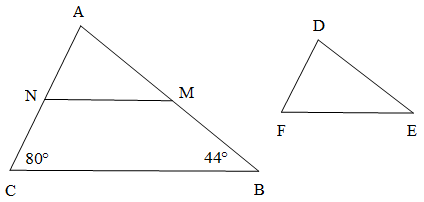
Bài 3. Cho hai tam giác ABC và DEF như hình vẽ. Biết MN // BC và ∆AMN = ∆DEF.

Tính:

a) Số đo góc DEF và góc NAM;

b) $\widehat{\text{FDE}}\text{+}\widehat{\text{DEF}}\text{+}\widehat{\text{NMB}}\text{=?}$

c) $\widehat{ANM}-\widehat{DEF}=?$

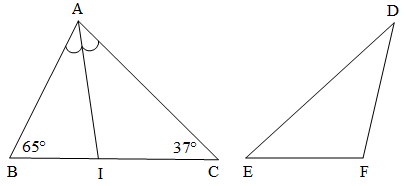
Bài 4. Cho hai tam giác ABC và DEF như hình vẽ. Biết rằng ∆AIC = ∆DEF và AI là tia phân giác góc BAC.

Tính:

a) Số đo góc BAC và góc DEF.

b) $\widehat{EDF}-\widehat{CAI}=?$

c) $\widehat{AIC}+\widehat{DEF}+\widehat{EDF}=?$

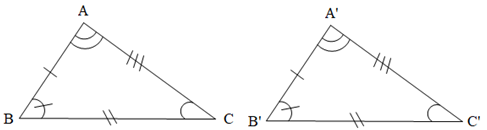
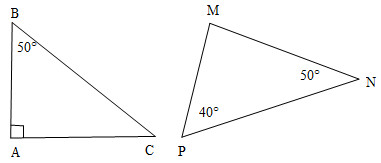
Bài 5. Cho hai tam giác ABC và MNP như hình vẽ. Biết rằng AB = MN, BC = NP, AC = MP.

a) Tính số đo góc ACB.

b) Tam giác MNP là tam giác gì?

c) Chứng minh ∆ABC = ∆MNP.