1. Công thức
a) Lũy thừa với số mũ tự nhiên
(x ∈ ℚ, n ∈ ℕ, n > 1);
Nếu (a, b ∈ ℤ, b ≠ 0) thì:
.
Quy ước:
(x ∈ ℚ, x ≠ 0);
(x ∈ ℚ).
b) Nhân hai lũy thừa cùng cơ số
xm .xn = xm+n (x ℚ, m, n ℕ);
c) Chia hai lũy thừa cùng cơ số
xm : xn = xm-n (x ≠ 0, m ≥ n);
d) Lũy thừa của lũy thừa
= xm.n (x ℚ, m, n ℕ).
2. Ví dụ minh họa
Ví dụ 1. Tính:
a) (–3)3;
b) ;
c) ;
d) .
Hướng dẫn giải:
a) (–3)3 = (–3).(–3).(–3)= –27;
b)
;
c)
;
d)
Ví dụ 2. Viết các biểu thức dưới dạng lũy thừa:
Hướng dẫn giải:
Ví dụ 3. Tìm x, biết:
a) x : 73 = 79 ;
b) ;
c) 25x : 52 = 54 .
Hướng dẫn giải:
a) x : 72 = 73
x = 73. 72
x = 75 = 1807
Vậy x = 1807.
b)
Vậy .
c) 25x : 52 = 54
(52)x = 54. 52
52x = 56
2.x = 6
x = 3
Vậy x = 3.
3. Bài tập tự luyện
Bài 1. Viết các số sau đây:
a) ; dưới dạng lũy thừa cơ số ;
b) 625; 3126 dưới dạng lũy thừa cơ số 5.
Bài 2. Không sử dụng máy tính, hãy tính:
a) (–3)8, biết (–3)7 = –2187;
b) , biết .
Bài 3. Viết các biểu thức sau dưới dạng lũy thừa của một số hữu tỉ:
a) (–2)8. (–2)4;
b) ;
c) (–125)3 : 253 .
Bài 4. Tính
a) ;
b) .
Bài 5. Viết các biểu thức sau dưới dạng lũy thừa của một số hữu tỉ:
a) 158. 24;
b) 275 : 323.

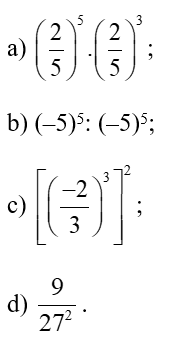
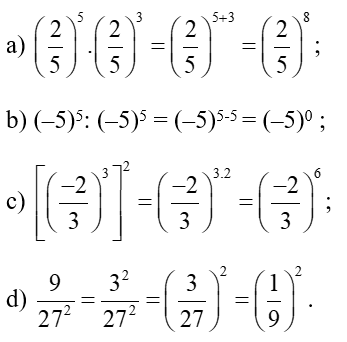
0 Comments:
Đăng nhận xét