
I. Số hữu tỉ là gì?
Trong toán học, cụ thể là đại số, số hữu tỉ là các số x có thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên với b khác 0.Tập hợp các số hữu tỉ, hay còn gọi là trường số hữu tỉ, có ký hiệu là Q.
Số hữu tỉ là số có thể viết dưới dạng a/b với a, b ∈ Z,b ≠ 0 và được kí hiệu là Q
Ví dụ: Các số 3; -1/2; 2/3;... là các số hữu tỉ
Định nghĩa của số hữu tỉ. (Ảnh: Sưu tầm Internet)
Tập hợp số hữu tỉ gồm:
Số thập phân hữu hạn: 0.5 (½), 0.2 (⅕),...Số thập phân vô hạn tuần hoàn: 0.16666… (⅙), 0.3333… (⅓),...
Tập hợp số nguyên (Z): -2, -1, 0, 1, 2,...
Tập hợp số tự nhiên (N): 1, 2, 3, 4, 5, 6,…
Tính chất của số hữu tỉ:
Tập hợp số hữu tỉ là tập hợp đếm được.Phép nhân số hữu tỉ có dạng
Phép chia số hữu tỉ có dạng:
Nếu số hữu tỉ là số hữu tỉ dương thì số đối của nó là số hữu tỉ âm và ngược lại. Tức tống số hữu tỉ và số đối của nó bằng 0.
II. Số vô tỉ là gì?
Trong toán học, các số vô tỉ là tất cả các số thực không phải là số hữu tỉ, mà là các số được xây dựng từ các tỷ số (hoặc phân số) của các số nguyên.
Các bạn cần ghi nhớ các số thực không phải là số hữu tỉ có nghĩa là các bạn không thể biểu diễn được dưới dạng tỉ số như a/ b (trong đó a, b là các số nguyên).
Ví dụ:
Số vô tỉ: 0,1010010001000010000010000001… (đây là số thập phân vô hạn không tuần hoàn)
Số căn bậc 2: √2 (căn 2)
Số pi (π): 3,14159 26535 89793 23846 26433 83279 50 288…..
Số vô tỉ kí hiệu là gì?
Số vô tỉ là các số viết được dưới dạng số thập phân vô hạn không tuần hoàn. Và kí hiệu của số vô tỉ là I.Các bạn cần ghi nhớ các số thực không phải là số hữu tỉ có nghĩa là các bạn không thể biểu diễn được dưới dạng tỉ số như a/ b (trong đó a, b là các số nguyên).
Tính chất của số vô tỉ:
Tập hợp số vô tỉ là tập hợp không đếm được.Ví dụ:
Số vô tỉ: 0,1010010001000010000010000001… (đây là số thập phân vô hạn không tuần hoàn)
Số căn bậc 2: √2 (căn 2)
Số pi (π): 3,14159 26535 89793 23846 26433 83279 50 288…..
III. Sự khác nhau giữa số hữu tỉ và số vô tỉ
Số hữu tỉ bao gồm số thập phân vô hạn tuần hoàn, còn số vô tỉ là các số thập phân vô hạn không tuần hoàn.
Số hữu tỉ chỉ là phân số, còn số vô tỉ có rất nhiều loại số khác nhau
Số hữu tỉ là số đếm được, còn số vô tỉ là số không đếm được
Số hữu tỉ chỉ là phân số, còn số vô tỉ có rất nhiều loại số khác nhau
Số hữu tỉ là số đếm được, còn số vô tỉ là số không đếm được
IV. Các loại số hữu tỉ phổ biến
Số hữu tỉ gồm những số nào?
Thì trong toán học sẽ có 2 loại số hữu tỉ, bao gồm số hữu tỉ âm và số hữu tỉ dương.
Cụ thể:
Số hữu tỉ âm: Bao gồm những số hữu tỉ nhỏ hơn 0
Số hữu tỉ dương: Bao gồm những sổ hữu tỉ lớn hơn 0
Lưu ý: số 0 không phải là số hữu tỉ âm và cũng không phải là số hữu tỉ dương.

Cụ thể:
Số hữu tỉ âm: Bao gồm những số hữu tỉ nhỏ hơn 0
Số hữu tỉ dương: Bao gồm những sổ hữu tỉ lớn hơn 0
Lưu ý: số 0 không phải là số hữu tỉ âm và cũng không phải là số hữu tỉ dương.

Số hữu tỉ âm và số hữu tỉ dương. (Ảnh: Sưu tầm Internet)
V. Các phép toán cơ bản với số hữu tỉ
Trong chương trình toán học lớp 7 trở lên, các em sẽ được làm quen với các phép toán cơ bản với số hữu tỉ như sau:
Bước 1: Viết các số hữu tỉ dưới dạng phân số
Bước 2: Áp dụng quy tắc cộng, trừ và các tính chất để tính
Quy tắc cộng, trừ: Đưa các số hữu tỉ về cùng mẫu (quy đồng, rút gọn,…) rồi cộng, trừ tử số, giữ nguyên mẫu số.
Tính chất:
Tính chất giao hoán: x + y = y + x
Tính chất kết hợp: (x + y) + z = x + (y + z)
Tính chất cộng với 0: x + 0 = 0 + x = x
Bước 3: Rút gọn kết quả (nếu có thể)
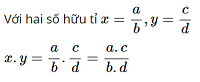
Chia hai số hữu tỉ:
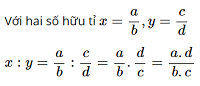
Nếu x > 0 thì |x| = x.
Nếu x = 0 thì |x| = 0.
Nếu x < 0 thì |x| = -x.Dựa vào định nghĩa trên, công thức xác định giá trị tuyệt đối của 1 số hữu tỉ như sau:
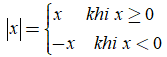
1. Phép tính cộng trừ
Sau đây là các bước mà bạn có thể áp dụng để tính các phép toán cộng trừ với các số hữu tỉ.Bước 1: Viết các số hữu tỉ dưới dạng phân số
Bước 2: Áp dụng quy tắc cộng, trừ và các tính chất để tính
Quy tắc cộng, trừ: Đưa các số hữu tỉ về cùng mẫu (quy đồng, rút gọn,…) rồi cộng, trừ tử số, giữ nguyên mẫu số.
Tính chất:
Tính chất giao hoán: x + y = y + x
Tính chất kết hợp: (x + y) + z = x + (y + z)
Tính chất cộng với 0: x + 0 = 0 + x = x
Bước 3: Rút gọn kết quả (nếu có thể)
2. Phép tính nhân chia
Nhân hai số hữu tỉ: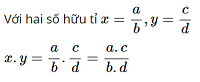
Chia hai số hữu tỉ:
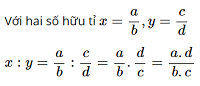
VI. Các phép tính và công thức toán khác với số hữu tỉ
Bên cạnh các phép tính cơ bản kể trên, thì các bạn còn cần phải lưu ý một số phép tính và công thức liên quan đến số hữu tỉ thường gặp sau.Giá trị tuyệt đối của 1 số hữu tỉ
Giá trị tuyệt đối của một số hữu tỉ x được kí hiệu là |x|, là khoảng cách từ điểm x tới điểm O trên trục số.Nếu x > 0 thì |x| = x.
Nếu x = 0 thì |x| = 0.
Nếu x < 0 thì |x| = -x.Dựa vào định nghĩa trên, công thức xác định giá trị tuyệt đối của 1 số hữu tỉ như sau:
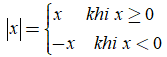
Công thức tính lũy thừa của 1 số hữu tỉ:
Các công thức tính lũy thừa của 1 số hữu tỉ mà bạn cần phải ghi nhớ:


Cách so sánh hai số hữu tỉ
Để so sánh hai số hữu tỉ x, y ta có thể làm như sau:
Viết x, y dưới dạng phân số cùng mẫu dương.
x = a /m; y = b/m ( m > 0)
Để so sánh hai số hữu tỉ x, y ta có thể làm như sau:
Viết x, y dưới dạng phân số cùng mẫu dương.
x = a /m; y = b/m ( m > 0)
So sánh các tử là số nguyên a và b
Nếu a > b thì x > y
Nếu a = b thì x = y
Nếu a < b thì x < y
VII. Các dạng bài tập về số hữu tỉ thường gặp và phương pháp giải
Dưới đây là một số dạng bài tập về số hữu tỉ thường gặp và phương pháp giải để các em tham khảo và áp dụng:
Dạng 1: Thực hiện phép tính
Phương pháp giải: Đầu tiên cần viết 2 số hữu tỉ đã cho dưới dạng phân số, rồi tiến hành áp dụng quy tắc tính toán để tính và đưa ra đáp số chính xác, cũng như rút gọn kết quả nếu có thể.Lưu ý: Chỉ được áp dụng tính chất:a.b + a.c = a.(b+c)
a.c + b.c = (a+b).c)
Chứ không được áp dụng: a:b + a:c = a:(b+c)
Ví dụ:
a) $\frac{-2}{3}+\frac{-1}{12}$
b) $\frac{11}{30}-\frac{1}{5}$;
c) $\frac{-5}{2}:\frac34$;
d) $4\frac{1}{5}:(-2\frac{2}{5})$
•Hướng dẫn
a) $\frac{-2}{3} + \frac {-1}{12} = \frac {-8}{12} + \frac {-1}{12}= \frac {-9}{12} = \frac {-3}{4}$
b) $\frac{11}{30} - \frac {1}{5} = \frac {11}{30} - \frac {6}{30}= \frac {5}{30} = \frac {1}{6}$
c) $\frac{-5}{2} \times \frac {3}{4} = \frac {-5}{2} \times \frac {4}{3} = \frac {-20}{6} = \frac {-10}{3}$
d) $\frac{21}{5} \times \frac {-12}{5} = \frac {21}{5} \times \frac {-5}{12} = \frac {-21}{12} = \frac {-7}{4}$
b) $\frac{11}{30} - \frac {1}{5} = \frac {11}{30} - \frac {6}{30}= \frac {5}{30} = \frac {1}{6}$
c) $\frac{-5}{2} \times \frac {3}{4} = \frac {-5}{2} \times \frac {4}{3} = \frac {-20}{6} = \frac {-10}{3}$
d) $\frac{21}{5} \times \frac {-12}{5} = \frac {21}{5} \times \frac {-5}{12} = \frac {-21}{12} = \frac {-7}{4}$
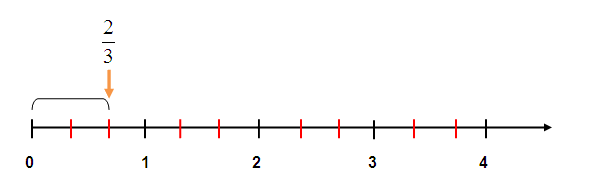
Dạng 2: Biểu diễn số hữu tỉ trên trục số
Phương pháp giải:
Trường hợp a/b là số hữu tỉ dương: ta tiến hành chia khoảng có độ dài 1 đơn vị làm b phần bằng nhau. Sau đó tiến hành lấy về chiều dương trục Ox với a phần. Lúc này ta sẽ được vị trí của số a/b.
Trường hợp a/b là số hữu tỉ âm: ta tiến hành chia khoảng có độ dài 1 đơn vị làm b phần bằng nhau. Sau đó tiến hành lấy về chiều âm trục Ox với a phần. Lúc này ta sẽ được vị trí của số a/b.
Ví dụ: Biểu diễn số 5/4
Giải:
Ta thấy 5/4 là số hữu tỉ dương. Lúc này ta chia các khoảng tương ứng với độ dài 1 đơn vị làm thành 4 phần bằng nhau. Lấy 5 phần ta sẽ biểu diễn được phân số 5/4.
Ví dụ: So sánh các số hữu tỉ sau:


Ví dụ:



Trường hợp a/b là số hữu tỉ âm: ta tiến hành chia khoảng có độ dài 1 đơn vị làm b phần bằng nhau. Sau đó tiến hành lấy về chiều âm trục Ox với a phần. Lúc này ta sẽ được vị trí của số a/b.
Ví dụ: Biểu diễn số 5/4
Giải:
Ta thấy 5/4 là số hữu tỉ dương. Lúc này ta chia các khoảng tương ứng với độ dài 1 đơn vị làm thành 4 phần bằng nhau. Lấy 5 phần ta sẽ biểu diễn được phân số 5/4.
Dạng 3: So sánh các số hữu tỉ
Phương pháp giải: Ta sẽ đưa các số hữu tỉ đã cho dưới dạng phân số có cùng mẫu số dương rồi so sánh tử số. Ngoài ra, các em cũng có thể so sánh với số 0, so sánh với số 1, -1 hay dựa vào phần bù của 1, cũng như so sánh với phân số trung gian để tìm đáp án chính xác.Ví dụ: So sánh các số hữu tỉ sau:


Dạng 4: Tìm điều kiện để một số hữu tỉ là âm, dương hoặc là 0
Phương pháp giải: Các em dựa vào tính chất của số hữu tỉ để xác định được đó là số âm, dương hay là 0.Ví dụ:


Dạng 5: tìm các số hữu tỉ nằm trong một khoảng
Phương pháp giải: Đưa các số hữu tỉ đó về cùng mẫu hoặc tử số.

Dạng 6: Tìm x để biểu thức nguyên
Phương pháp giải: Trường hợp tử số không chứa x ta dùng dấu chia hết, nếu tử số chứa x ta dùng dấu chia hết hoặc áp dụng cách tách tử số theo mẫu số. Đối với những bài toán tìm đồng thời cả x và y, ta sẽ nhóm x hoặc y rồi rút chúng đưa về dạng phân thức.


Dạng 7: Các bài toán tìm x với số hữu tỉ
Phương pháp giải: Đầu tiên ta phải quy đồng khử mẫu số, rồi chuyển những số hạng chứa x về một vế, các số hạng còn lại về một vế (chuyển vế đổi dấu) rồi tiến hành tìm x.
Ví dụ:




Ví dụ:


Dạng 8: Bài toán tìm x trong các bất phương trình
Phương pháp giải:

Quy tắc 1: Tính tổng dãy số với những số hạng cách nhau một số không đổi
Phương pháp giải:


* Quy tắc 2: Tính tổng dãy số với những số hạng có số đứng sau gấp n số đứng trước.
Phương pháp giải: Tiến hành phân tích từ số thành hiệu của 2 số (số cuối – số đầu) phía mẫu số.












Phương pháp giải:


* Quy tắc 2: Tính tổng dãy số với những số hạng có số đứng sau gấp n số đứng trước.
Phương pháp giải: Tiến hành phân tích từ số thành hiệu của 2 số (số cuối – số đầu) phía mẫu số.

VIII. Một số bài tập mẫu về số hữu tỉ tự luyện













0 Comments:
Đăng nhận xét