TN T7. 15 Bài tập Tập hợp các số hữu tỉ

 

Câu 1:

• ℚ;
• ℕ
• ℤ
• ℝ

Tập hợp số hữu tỉ được kí hiệu là ℚ.

Câu 2:

• $\frac {a}{b}$với a, b ∈ ℕ;
• $ \frac {a}{b}$với a, b ∈ ℤ;
• $ \frac {a}{b}$với a, b ∈ ℕ, b ≠ 0;
• $\frac {a}{b}$với a, b ∈ ℤ, b ≠ 0/

Số hữu tỉ là số viết được dưới dạng phân số $\frac {a}{b}$với a, b ∈ ℤ, b ≠ 0.

Câu 3: Số không phải số hữu tỉ là

• $ \frac {-1}{2}$
• $ \frac {3}{0}$
• $ 3\frac {5}{8}$
• 1,5

Số hữu tỉ được viết dưới dạng $\frac {a}{b}$ với a, b ∈ ℤ, b ≠ 0.

Nên $ \frac {-1}{2}$ là số hữu tỉ.
Các số $ 3\frac {5}{8}$; 1,5 cũng là số hữu tỉ vì đều viết được dưới dạng $\frac {a}{b}$ với a, b ∈ ℤ, b ≠ 0;
$ 3\frac {5}{8}$ = $ \frac {29}{8}$
1,5 = $ \frac {3}{2}$.
$ \frac {3}{0}$ không là số hữu tỉ vì có mẫu số bằng 0.

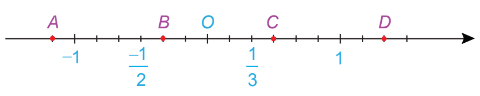
Câu 4: Các điểm B, C lần lượt biểu diễn những số hữu tỉ nào?

• $ \frac {-1}{3}$, $ \frac {1}{2}$
• $ \frac {1}{3}$, $ \frac {1}{2}$
• $ \frac {-1}{3}$, $ \frac {1}{4}$
• $ \frac {-1}{3}$, $ \frac {1}{6}$

Đoạn thẳng từ điểm O đến 1 được chia thành 6 phần bằng nhau.
Đoạn thẳng OB chiếm 2 phần; B nằm trước O nên biểu diễn số hữu tỉ âm.

Vậy điểm B biểu diễn số hữu tỉ là $ \frac {-2}{6}$ = $ \frac {-1}{3}$.

Đoạn thẳng OC chiếm 3 phần; C nằm sau O nên biểu diễn số hữu tỉ dương.

Vậy điểm C biểu diễn số hữu tỉ là $ \frac {3}{6}$ = $ \frac {1}{2}$.

Câu 5: Số đối của số hữu tỉ $ \frac {7}{2}$ là

• $ \frac {-7}{2}$
• $ \frac {2}{7}$
• $ \frac {-2}{7}$
• 3,5

Số đối của số hữu tỉ $ \frac {7}{2}$là $ \frac {-7}{2}$.

Câu 6: Số hữu tỉ có thể là

• số thập phân có thể viết dưới dạng phân số thập phân;
• số nguyên;
• hỗn số;
• Cả A, B và C đều đúng.

Số hữu tỉ có thể là số thập phân có thể viết dưới dạng phân số thập phân (ví dụ 0,3 = $\frac {3}{10}$);
số nguyên (ví dụ 2 = $ \frac {2}{1}$);
hỗn số (ví dụ $ 3\frac {5}{8}$ = $ \frac {29}{8}$).

Câu 7: Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau

• nằm về cùng một phía so với điểm O;
• nằm về hai phía khác nhau so với điểm O;
• nằm về hai phía khác nhau so với điểm O và có cùng khoảng cách đến O;
• trùng nhau.

Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau nằm về hai phía khác nhau so với điểm O và có cùng khoảng cách đến O.

Câu 8: Điểm biểu diễn số đối của của số hữu tỉ $\frac{-2}{1}$là

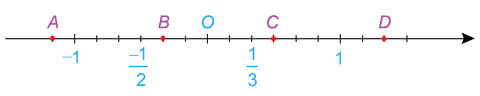
• điểm A
• điểm B
• điểm C;
• điểm D

Điểm biểu diễn số hữu tỉ đối của $\frac{-1}{2}$ nằm khác phía với so với điểm O. Như vậy điểm này nằm sau O.
Khoảng cách tử O đến $\frac{-1}{2}$là 3 đoạn nên khoảng cách từ O đến điểm đó cũng là 3 đoạn.
Vậy điểm biểu diễn số hữu tỉ đối của $\frac{-1}{2}$ là điểm C.

Câu 9: Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì:

• a = c;
• a < c;
• a > c;
• a ≤ c

Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

Câu 10: Trên trục số, nếu a < b thì

• điểm a trùng với điểm b;
• điểm a nằm sau điểm b;
• điểm b nằm trước điểm a.
• điểm a nằm trước điểm b;

Trên trục số, nếu a < b thì điểm a nằm trước điểm b.

Câu 11: Cho hai số hữu tỉ a và b được biểu diễn trên trục số như sau

Khẳng định đúng nhất là

• b < 0 < a.
• b > 0 > a;
• b > a;
• b < a < 0;

Ta có: b nằm trước O nên b < 0; a nằm sau O nên a > 0. Do đó: b < 0 < a.

Câu 12: Trong các số hữu tỉ: ; ; 0,75; . Số lớn nhất là

• -1$\frac{1}{2}$
• -5
• 0,75
• $\frac{4}{5}$

Ta có: -1$\frac{1}{2}$= $\frac{-3}{2}$ ;
-5 = -$\frac{10}{2}$
mà -$\frac{10}{2}$ < $\frac{-3}{2}$ < 0 nên -5 < -1$\frac{1}{2}$ , 0;
0,75 = $\frac{3}{4}$ = $\frac{15}{20}$;
$\frac{4}{5}$ = $\frac{16}{20}$ > $\frac{15}{20}$ > 0 nên $\frac{4}{5}$ > 0,75 > 0.
Do đó -5 < -1$\frac{1}{2}$ < 0,75 < $\frac{4}{5}$

Câu 13: Dãy các số hữu tỉ được sắp xếp theo chiều tăng dần là

• $\frac{7}{25}$; $\frac{8}{125}$; $\frac{-1}{9}$; $\frac{-5}{27}$
• $\frac{-1}{9}$; $\frac{-5}{27}$; $\frac{7}{25}$; $\frac{8}{125}$
• $\frac{-5}{27}$; $\frac{-1}{9}$; $\frac{8}{125}$; $\frac{7}{25}$
• $\frac{8}{125}$; $\frac{7}{25}$; $\frac{-1}{9}$; $\frac{-5}{27}$

Ta có:
$\frac{-1}{9}$; $\frac{-3}{27}$ mà $\frac{-3}{27}$ > $\frac{-5}{27}$ >0 nên $\frac{-1}{9}$ > $\frac{-5}{27}$ >0.
$\frac{7}{25}$ = $\frac{35}{125}$ mà $\frac{35}{125}$ > $\frac{8}{125}$ > 0
Do đó: $\frac{-5}{27}$ < $\frac{-1}{9}$ < $\frac{8}{125}$ < $\frac{7}{25}$.

Câu 14: So sánh đúng là

• $\frac{2020}{2021}$ > $\frac{2021}{2022}$
• $\frac{2020}{2021}$ < $\frac{2021}{2022}$
• $\frac{2020}{2021}$ = $\frac{2021}{2022}$
• không so sánh được

Ta có: $\frac{2020}{2021}$ + $\frac{1}{2021}$ = 1
$\frac{2021}{2022}$ + $\frac{1}{2022}$ = 1.
mà $\frac{1}{2021}$ > $\frac{1}{2022}$ nên $\frac{2020}{2021}$ < $\frac{2021}{2022}$

Câu 15: Phân số biểu diễn số hữu tỉ -0,625

• $\frac{-5}{8}$
• $\frac{-6}{25}$
• $\frac{6}{25}$
• $\frac{-625}{100}$

0,625 = $\frac{-625}{100}$ = $\frac{-5}{8}$

Hãy trả lời các câu hỏi để biết kết quả của bạn