Toán lớp 8 có khối lượng kiến thức khá lớn khiến các em học sinh gặp nhiều khó khăn để ghi nhớ. Trong bài chia sẻ này, Mathnasium sẽ hệ thống hóa toàn bộ kiến thức hình học lớp 8 để giúp đỡ trẻ ôn luyện, học tập tại nhà hiệu quả hơn.
Kiến thức Hình học lớp 8 Chương 1
Nội dung của chương học này gồm các phần quan trọng dưới đây:
Tứ giác
- Định nghĩa: Tứ giác ABCD là hình có 4 cạnh: AB, BC, CD, DA, trong đó không có bất kì hai đoạn thẳng nào cùng nằm trên một đường thẳng.
- Nhận biết: Tứ giác lồi là tứ giác có cả 4 cạnh nằm hoàn toàn trong một nửa mặt phẳng lấy bờ là đường thẳng cạnh bất kì của tam giác. Tứ giác lõm là tứ giác có ít nhất 1 cạnh khi lấy làm bờ mặt phẳng sẽ có các cạnh còn lại không thuộc cùng một nửa mặt phẳng.
- Định lí: Tổng các góc trong của một tứ giác là 360 độ.
- Tính chất: Góc kề bù liền với một góc bất kỳ trong tứ giác gọi là góc ngoài của tứ giác. Tổng số đo các góc ngoài của tứ giác tại một góc bất kỳ luôn bằng 360 độ.
Hình thang
ABCD là hình thang nếu có:
- AB // CD
- Tổng các góc trong bằng 180 độ
- hai cặp cạnh đối diện song song và bằng nhau.
- Nếu có một góc vuông, sẽ là hình thang vuông.
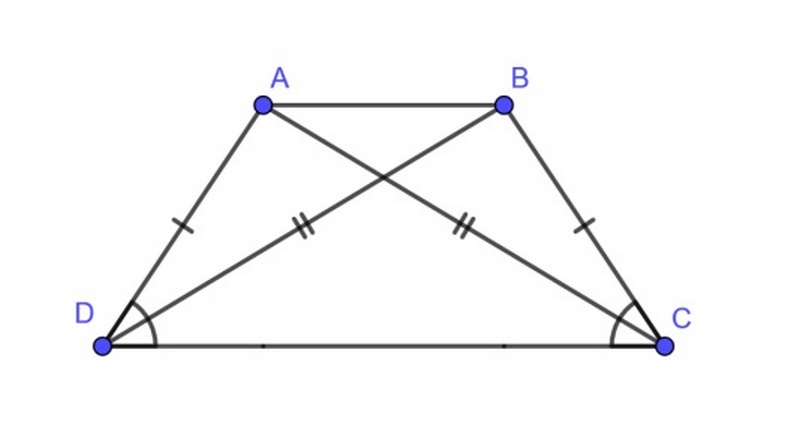
Hình thang cân
- Định nghĩa: Hình thang cân là hình thang có hai góc liền kề một cạnh đáy bằng nhau. Hai góc đối nhau trong hình thang cân bằng 180 độ.
- Tính chất: ABCD là hình thang cân thì cạnh AD = BC; AC = BD.
Đường trung bình trong tam giác, trong hình thang
- Đường trung bình trong tam giác là đoạn thẳng nối liền trung điểm hai cạnh bất kỳ của tam giác.
- Đường trung bình trong hình thang là đoạn thẳng nối liền trung điểm hai cạnh bên đối diện nhau của hình thang.
Hình bình hành
Hình bình hành là tứ giác có 2 cặp cạnh đối nhau song song và bằng nhau.
Dấu hiệu nhận biết một hình là hình bình hành:
- Tứ giác có các cạnh đối nhau song song và bằng nhau
- Tứ giác có các góc đối bằng nhau sẽ là hình bình hành.
- Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường là hình bình hành.
Hình chữ nhật
Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông.
Tính chất của hình chữ nhật:
- Hình chữ nhật sở hữu tất cả các tính chất mà hình hành, hình thang cân sở hữu
- Trong hình chữ nhật, hai đường chéo luôn bằng nhau và giao nhau tại trung điểm mỗi đường.
Dấu hiệu nhận biết hình chữ nhật:
- Tứ giác có ba góc vuông là hình chữ nhật
- Hình thang cân có một góc vuông là hình chữ nhật
- Hình bình hành có một góc vuông là hình chữ nhật
- Hình bình hành có hai đường chéo giao nhau, chiều dài bằng nhau là hình chữ nhật.
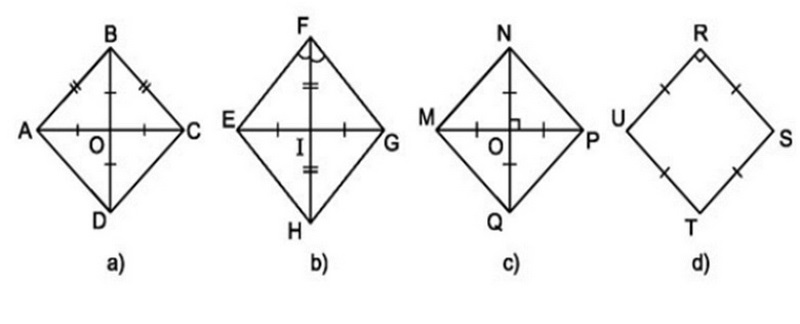
Hình thoi
Định nghĩa: Hình thoi là tứ giác có bốn cạnh độ dài bằng nhau. Hình thoi cũng có thể là một hình bình hành với các góc đối nhau bằng nhau
Tính chất: Hình thoi có tất cả các tính chất hình bình hành sở hữu
Dấu hiệu nhận biết:
- Tứ giác có bốn cạnh bằng nhau không nhất định 2 cạnh đối nhau song song là hình thoi.
- Hình bình hành nếu có hai cạnh kề độ dài bằng nhau là hình thoi.
- Hình bình hành nếu có hai đường chéo vuông góc thì là hình thoi.
- Hình bình hành nếu có một đường chéo đi qua trung điểm đường chéo còn lại, hay đi qua đường phân giác của một góc thì đó là hình thoi.
Hình vuông
Định nghĩa: Hình tứ giác có bốn góc vuông và bốn cạnh bằng nhau thì là hình vuông.
Tính chất:
- Hình vuông là hình chữ nhật sở hữu bốn cạnh bằng nhau.
- Hình vuông là hình thoi sở hữu một góc vuông.
- Hình vuông vừa là hình chữ nhật, vừa chính là hình thoi. Hình vuông sở hữu mọi tính chất hình chữ nhật và hình thoi sở hữu
- 2 đường chéo của hình vuông luôn bằng nhau và vuông góc với nhau
Dấu hiệu nhận biết:
- Hình chữ nhật có hai cạnh liền kề bằng nhau là hình vuông.
- Hình chữ nhật có hai đường chéo bằng nhau và vuông góc là hình vuông
- Hình chữ nhật có đường chéo chính là đường phân giác của góc đối diện là hình vuông
- Hình thoi sở hữu một góc vuông là hình vuông
- Hình thoi có hai đường chéo chiều dài bằng nhau là hình vuông.
Kiến thức Toán Hình học lớp 8 Chương 2
Nội dung chương 2 chủ yếu gồm các công thức tính diện tích, chu vi các hình học đã làm quen, hiểu rõ ở chương 1. Chi tiết các công thức nhu sau:
Đa giác
Đa giác lồi là đa giác nếu lấy một đường thẳng bất kì chứa cạnh nào đó của đa giác làm bờ sẽ có toàn bộ đa giác nằm trong một nửa mặt phẳng. Đa giác đều là đa giác có mọi cạnh bằng nhau, các góc bằng nhau. Như vậy hình vuông, hình tam giác đều là các đa giác đều.
Diện tích đa giác
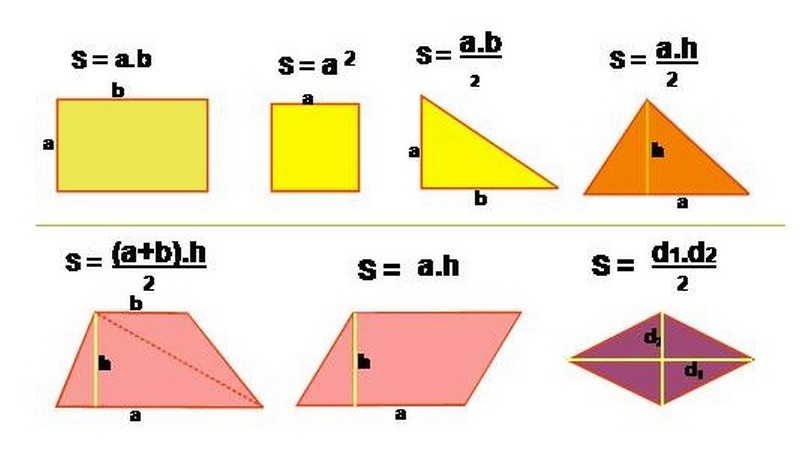
Công thức có trong nội dụng phần này bao gồm:
- Diện tích hình chữ nhật: S = a. b
- Diện tích tam giác: S = 1/2.a.h
- Diện tích tam giác vuông: S = 1/2.a.h
- Diện tích hình thang: S = [(a+b)xh]/2
- Diện tích hình bình hành: S = ah
- Diện tích hình thoi: S = 1/2.d1.d2

0 Comments:
Đăng nhận xét