Bài tập Chương 3 HH _ Bài 5 Hình chữ nhật - Hình vuông

Bài 1 trang 71 SBT Toán 8 tập 1 CTST: Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC.
Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh tứ giác ABDC là hình chữ nhật.
b) Gọi E là điểm đối xứng của A qua B. Chứng minh tứ giác BEDC là hình bình hành.
c) EM cắt BD tại K. Chứng minh EK = 2KM.

a) Xét tứ giác ABDC có: AM = MD (M ∈ AD); BM = MC (M ∈ BC).

Suy ra tứ giác ABDC là hình bình hành.

Ta có $\widehat{BAC} = 90^{\circ}$ (do ∆ABC vuông tại A).

Do đó, tứ giác ABDC là hình chữ nhật.

b) Tứ giác ABDC là hình chữ nhật (theo câu a), suy ra AB = CD và AB // CD.

Do E đối xứng với A qua B nên B, A, E thẳng hàng và AB = BE.

Vì AB // CD nên BE // CD.

Vì AB = CD và AB = BE nên CD = BE.

Xét tứ giác BEDC có BE // CD và BE = CD nên là hình bình hành.

c) ∆AED có hai đường trung tuyến EM và DB cắt nhau tại K, nên K là trọng tâm của tam giác AED.

Suy ra $EK =\frac{2}{3}EM $ và $KM = \frac{2}{3} EM$ nên $EK = 2KM$

Bài 2 trang 71 SBT Toán 8 tập 1 CTST: Cho tam giác DEF vuông tại D (DE > DF), DM là đường trung tuyến (M ∈ EF). Gọi MN là đường vuông góc kẻ từ M đến DE (N ∈ DE), MK là đường vuông góc kẻ từ M đến DF (K ∈ DF), H là điểm đối xứng với M qua N.

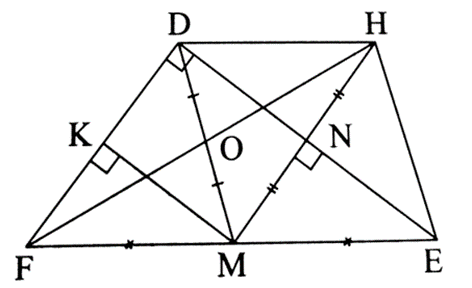
a) Tứ giác DKMN là hình gì Vì sao?

b) Gọi O là trung điểm của DM. Chứng minh ba điểm H, O , F thẳng hàng.

c) Tam giác DEF cần thêm điều kiện gì để tứ giác DKMN là hình vuông?

Giải

a) Do MN ⊥ DE tại N, MK ⊥ DF tại K nên và

Tứ giác DKMN có nên DKMN là hình chữ nhật.

b) ∆DEF vuông tại D và DM là đường trung tuyến ứng với cạnh huyền nên

Suy ra ∆MDE cân tại M.

Ta lại có MN ⊥ DE tại N, suy ra đường cao MN cũng đồng thời là đường trung tuyến của ∆MDE, suy ra .

Tứ giác DHEM có: ND = NE và NH = NM (do H là điểm đối xứng với M qua N).

Suy ra DHEM là hình bình hành.

Do đó DH // ME và DH = ME.

Mà M là trung điểm EF nên ME = MF

Khi đó DH // MF và DH = MF nên tứ giác DHMF là hình bình hành.

Hơn nữa, O là trung điểm của DM, suy ra O cũng là trung điểm của HF.

Vậy H, O, F thẳng hàng.

c) Hình chữ nhật DKMN là hình vuông khi DM là đường phân giác của , hay DM là đường phân giác của .

Khi đó DM là đường trung tuyến và cũng là đường phân giác xuất phát từ D của ∆DEF

Do đó ∆DEF cân tại D

Suy ra ∆DEF vuông cân tại D.

Vậy ∆DEF vuông cân tại D thì DKMN là hình vuông.

Bài 3 trang 71 SBT Toán 8 tập 1 CTST: Cho tam giác ABC vuông tại A, AB = 4 cm, AC = 8 cm. Gọi E là trung điểm của AC, M là trung điểm của BC. a) Tính EM. b) Vẽ tia Bx song song với AC sao cho Bx cắt EM tại D. Chứng minh tứ giác ABDE là hình vuông. c) Gọi I là giao điểm của BE và AD, K là giao điểm của BE và AM. Chứng minh tứ giác BDCE là hình bình hành và DC= 6KI.

Giải

a) ∆ABC có E là trung điểm của AB, M là trung điểm của BC (giả thiết).

Ta có $ME = \frac{1}{2}AB$ và ME // AB

Do đó $ME = \frac{1}{2}AB = \frac{1}{2}.4=2 (cm)$

b) Tứ giác ABDE có: AB // DE (do AB // ME) và BD // AE (do Bx // AC ).

Suy ra ABDE là hình bình hành.

Hình bình hành ABDE có $\widehat{BAE} = 90^{\circ}$ (do ∆ABC vuông tại A) nên ABDE là hình chữ nhật.

Ta lại có $AE=\frac{1}{2}AC$ (do E là trung điểm của AC), suy ra $AE = \frac{1}{2} .8 = 4 (cm)$

Khi đó AB = AE = 4 (cm).

Hình chữ nhật ABDE có AB = AE nên ABDE là hình vuông.

c) Hình vuông ABDE có AD cắt BE tại I, suy ra I là trung điểm của AD và BE.

Xét ∆ADC có I là trung điểm AD, E là trung điểm AC

Theo bài 4, trang 63, SBT Toán 8 Tập Một, ta có: IE // CD và $IE = \frac{1}{2}CD$

Tứ giác BDCE có: BE // CD (vì IE // CD); BD // EC (vì Bx // AC).

Suy ra BDCE là hình bình hành.

Do đó, hai đường chéo BC và DE cắt nhau tại trung điểm của mỗi đường.

Mà M là trung điểm của BC, suy ra M cũng là trung điểm của DE.

∆ADE có đường trung tuyến AM và EI cắt nhau tại K nên K là trọng tâm của ∆ADE.

Suy ra $KI = \frac{1}{3}EI = \frac{1}{3}.(\frac{1}{2}EB)= \frac{1}{6}EB = \frac{1}{6}DC$ 

Vậy DC = 6KI.

Bài 4 trang 72 SBT Toán 8 tập 1 CTST: Cho tam giác ABC cân tại A ($\widehat{A} < 90^{\circ}$), các đường cao BD và CE cắt nhau tại H. Tia phân giác của góc ABD cắt EC và AC lần lượt tại M và P. Tia phân giác của góc ACE cắt DB và AB lần lượt tại Q và N. Chứng minh rằng: 

a) $\widehat{ABD} = \widehat{ACE}$

b) BH = CH;

c) Tam giác BOC vuông cân;

d) MNPQ là hình vuông.

Giải

a) Ta có:

∆ABD vuông tại D (do BD là đường cao ∆ABC), suy ra $\widehat{ABD} + \widehat{BAC} = 90^{\circ}$

∆AEC vuông tại E (do CE là đường cao ∆ABC), suy ra $\widehat {ACE} + \widehat{BAC} = 90^{\circ}$

Do đó $\widehat{ABD} = \widehat{ACE}$

b) ∆ABC cân tại A nên $\widehat{ABC} = \widehat{ACB}$

Mà $\widehat{ABD} = \widehat{ACE}$

Suy ra $\widehat{ABC} -\widehat{ABD} = \widehat{ACB} - \widehat{ACE}$ hay $\widehat{B_{3}} = \widehat{C_{3}}$

Do đó ∆HBC cân tại H nên BH = CH.

c) Ta có $\widehat{B_{2}} = \frac{1}{2} \widehat{ABD}$ (do BP là tia phân giác $\widehat{ABD}$ và $\widehat{C_{2}} = \frac{1}{2} \widehat{ACE}$ do CN là tia phân giác $\widehat{ACE}$)

Mà $\widehat{ABD} = \widehat{ACE}$ suy ra $\widehat{B_{2}}=\widehat{C_{2}}$

∆OBC có $\widehat{B_{3}}=\widehat{C_{3}}, \widehat{B_{2}}=\widehat{C_{2}}$ nên  $\widehat{B_{3}}+\widehat{B_{2}} =  \widehat{C_{3}}+\widehat{C_{2}}$ hay $\widehat{OBC} = \widehat{OCB}$

Suy ra ∆OBC cân tại O (1)

Mặt khác vì $\widehat{C_{2}} =\widehat{B_{1}}$ (cùng bằng $\widehat{B_{2}}$) nên ta có 

$\widehat{B_{3}}+\widehat{B_{2}}  +\widehat{C_{3}}+\widehat{C_{2}}=\widehat{B_{3}}+\widehat{B_{2}} + \widehat{B_{1}}+\widehat{B_{3}}  $

= $ \widehat{EBC} + \widehat{ECB} = 180^{\circ} - \widehat{BEC} =  180^{\circ} - 90^{\circ} =  90^{\circ}$

Mà $ \widehat{OBC} +  \widehat{OCB} = \widehat {B_{2}} +  \widehat {B_{3}} + \widehat {C_{2}}+ \widehat {C_{3}} = 90^{\circ}$

Suy ra $ \widehat{BOC} = 180^{\circ} - (  \widehat{OBC} +  \widehat{OCB}) = 180^{\circ} - 90^{\circ} =  90^{\circ}$

Do đó tam giác OBC vuông tại O (2)

Từ (1) và (2) suy ra ∆OBC vuông cân tại O.

d) ∆OBC cân tại O nên OB = OC. (3)

Xét ∆BMH và ∆CQH có:

$\widehat{B_{2}}+\widehat{C_{2}}  $

BH = CH (do ∆HBC cân tại H);

$\widehat{BHM}+\widehat{CHQ} $ (hai góc đối đỉnh).

Do đó ∆BMH= ∆CQH (g.c.g).

Suy ra BM = CQ. (4)

Từ (3) và (4) suy ra OB ‒ BM = OC ‒ CQ hay OM = OQ. (5)

Mà ∆BNQ có BO là đường cao cũng đường phân giác nên ∆BNQ cân tại B.

Suy ra BO cũng là đường trung tuyến, nên O là trung điểm của QN hay ON = OQ.(6)

Chứng minh tương tự, ta được OP = OM. (7)

Từ (5), (6), (7) suy ra OM = ON = OQ = OP.

Khi đó ON + OQ = OM + OP hay NQ = MP.

Xét tứ giác MNPQ có: OM = OP và OQ = ON nên tứ giác MNPQ là hình bình hành.

Mà NQ = MP nên MNPQ là hình chữ nhật.

Ta lại có MP ⊥ NP tại O nên MNPQ là hình vuông.

Bài 5 trang 72 SBT Toán 8 tập 1 CTST: Cho hình vuông ABCD. Lấy các điểm E, F, G, H theo thứ tự thuộc các cạnh AB, BC, CD, DA, sao cho AE = BF = CG = DH = a, BE = CF = DG = AH = b.
a) Tứ giác EFGH là hình gì?
b) Tính diện tích tư giác EFGH theo a và b.

Giải

a) Xét các tam giác HAE, EBF, FCG, GDH có:

AE = BF = CG = DH = a, BE = CF = DG = AH = b (giả thiết);

$\widehat{A} = \widehat{B} = \widehat{C} = \widehat{D} = 90^{\circ}$ (do ABCD là hình vuông)

Suy ra ∆HAE = ∆EBF = ∆FCG = ∆GDH (c.g.c) nên HE = EF = FG = GH

Do đó EFGH là hình thoi.

Ta lại có

$\widehat{E_{1}} + \widehat{E_{2}} = \widehat{E_{1}} + \widehat{H_{1}} = 90^{\circ}$ nên $\widehat{E_{3}} = 90^{\circ}$

Hình thoi EFGH có $\widehat{E_{3}} = 90^{\circ}$ nên EFGH là hình vuông.

b)Ta có $S_{ABCD} = AB^{2} = (a + b)^{2}$ (1)

$S_{\Delta HAE} = \frac{1}{2} AE . AH = \frac{1}{2}ab$

nên $S_{\Delta HAE}   + S_{\Delta EBF} + S_{\Delta FCG} + S_{\Delta GDH} = \frac{1}{2} ab.4 = 2ab$ (2)

Từ (1) và (2) suy ra $S_{EFGH} = (a + b)^{2} ‒ 2ab = a^{2} + 2ab + b^{2} – 2ab = a^{2} + b^{2}$.

Bài 6 trang 72 SBT Toán 8 tập 1 CTST: Trong hình chữ nhật có chu vi 100 m, hình nào có diện tích lớn nhất? Tính diện tích đó.

Giải

Gọi một kích thước của hình chữ nhật là x (m).

Do chu vi hình chữ nhật là 100 m nên ta có kích thước cạnh còn lại của hình chữ nhật là

$\frac{100}{2} - x = 50 -x $ (m)

Diện tích hình chữ nhật là:

$S = x(50 ‒ x) = ‒x^{2} + 50x$

$= ‒(x^{2} – 2.25x + 25^{2} ‒ 25^{2}) = ‒(x ‒ 25)^{2} + 625 ≤ 625.$

Giá trị lớn nhất của S bằng 625 tại x = 25.

Khi đó độ dài hai cạnh của hình chữ nhật là 25 m và 50 – 25 = 25 m, nên hình chữ nhật này là hình vuông.

Vậy diện tích lớn nhất của hình chữ nhật bằng 625 $m^{2}$, khi đó hình chữ nhật là hình vuông có cạnh dài 25 m.

Bài 7 trang 72 SBT Toán 8 tập 1 CTST: Hình chữ nhật ABCD được chia thành bốn hình chữ nhật nhỏ như Hình 10. Biết diện tích ba hình chữ nhật nhỏ lần lượt là 10 $cm^{2} , 15 cm^{2}, 6 cm^{2}$. Tính diện tích x ($cm^{2}$) của hình chữ nhật nhỏ còn lại.

Giải

Đặt AE = a; EB = b; AG = c; GD = d.

Do diện tích ba hình chữ nhật nhỏ lần lượt là 10 $cm^{2}$ , 15 $cm^{2}$, 6 $cm^{2}$ nên ta có:

ac= 10; bc = 6; ad =15.

Suy ra ac.bc.ad = 10.6.15, nên $(ac)^{2}$bd = 9000

Hay $10^{2}.bd = 9 000$, do đó bd = 9.

Vậy x = bd = 9 $cm^{2}$.

Lý thuyết Hình chữ nhật - Hình vuông SGK Toán 8 - Chân trời sáng tạo

Giải mục 1 trang 82, 83, 84 SGK Toán 8 tập 1– Chân trời sáng tạo
Giải mục 2 trang 84, 85, 86 SGK Toán 8 tập 1– Chân trời sáng tạo
Giải bài 1 trang 87 SGK Toán 8 tập 1– Chân trời sáng tạo
Giải bài 2 trang 87 SGK Toán 8 tập 1– Chân trời sáng tạo
Giải bài 3 trang 87 SGK Toán 8 tập 1– Chân trời sáng tạo
Giải bài 4 trang 87 SGK Toán 8 tập 1– Chân trời sáng tạo
Giải bài 5 trang 87 SGK Toán 8 tập 1– Chân trời sáng tạo

 

 

0000