Câu 1: Hãy chọn câu sai.
- Hình thang là tứ giác có hai cạnh đối song song.
- Nếu hình thanh có hai cạnh bên song song thì tất cả các cạnh của hình thang bằng nhau.
- Nếu một hình thang có hai cạnh đáy bằng nhau thị hai cạnh bên bằng nhau, hai cạnh bên song song.
- Hình thang vuông là hình thang có một góc vuông.
+ Hình thang là tứ giác có hai cạnh đối song song nên A đúng.
+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau nên B sai vì cạnh bên và cạnh đáy chưa chắc bằng nhau.
+ Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau nên C đúng.
+ Hình thang vuông là hình thang có một góc vuông nên D đúng.
Câu 2: Hình thang cân là hình thang có tính chất nào trong số các tính chất dưới đây?
- Có bốn cạnh song song với nhau.
- Có hai đường chéo vuông góc với nhau.
- Có hai góc kề một đáy bằng nhau.
- Có bốn cạnh bằng nhau.
Câu 3: Câu nào sau đây là đúng khi nói về hình thang:
- Hình thang là tứ giác có hai cạnh đối bằng nhau
- Hình thang là tứ giác có hai cạnh kề bằng nhau
- Hình thang là tứ giác có hai cạnh đối song song.
- Cả A, B, C đều sai
Theo định nghĩa: ”Hình thang là tứ giác có hai cạnh đối song song”
Câu 4: Chọn câu đúng nhất.
- Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
- Trong hình thang cân, hai cạnh bên bằng nhau.
- Trong hình thang cân, hai đường chéo bằng nhau
- Cả A, B, C đều đúng
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
+ Trong hình thang cân, hai cạnh bên bằng nhau.
+ Trong hình thang cân, hai đường chéo bằng nhau.
Vậy cả A, B, C đều đúng
Câu 5: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho AD = AE. Tứ giác BDEC là hình gì?
- Hình thang
- Hình thang cân
- Hình thang vuông
- Cả A, B, C đều sai
Tam giác ADE có AD = AE (gt) nên tam giác ADE cân tại A.
Suy ra $\widehat{A
D
E}$ = $\widehat{A
E
D}$ =
(
180
°
− $\widehat{D
A
E}$ )
÷
2
(1)
Tam giác ABC cân tại A (gt) nên $\widehat{A
B
C}$ = $\widehat{A
C
B}$ =
(
180
°
− $\widehat{B
A
C}$ )
÷
2
(2)
Từ (1) và (2) suy ra $\widehat{A
D
E}$ = $\widehat{A
B
C}$ Mà 2 góc này là hai góc ở vị trí đồng vị nên suy ra DE // BC
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang
Lại có $\widehat{A
B
C}$ =$\widehat{A
C
B}$ (vì tam giác ABC cân tại A) nên BDEC là hình thang cân
Câu 6: Góc kề cạnh bên của hình thang có số đo là 130°. Góc kề còn lại của cạnh bên đó là:
- 70°
- 100°
- 40°
- 50°
Vì tổng hai góc ké cạnh bên của hình thang bằng 180° nên góc kẻ còn lại của cạnh bên đó có số đo bằng 180° - 130° = 50°.
Câu 7: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho AD = AE. Tứ giác BDEC là hình gì?
- Hình thang
- Hình thang cân
- Hình thang vuông
- Cả A, B, C đều sai
Tam giác ADE có AD = AE (gt) nên tam giác ADE cân tại A.
Suy ra $\widehat{A
D
E} = {A
E
D} =
(
180
°
− {D
A
E}$ )
÷
2
(1)
Tam giác ABC cân tại A (gt) nên $\widehat{A
B
C} = {A
C
B}$ =
(
180
°
− $\widehat{B
A
C}$ )
÷
2
(2)
Từ (1) và (2) suy ra $\widehat{A
D
E} = {A
B
C}$
Mà 2 góc này là hai góc ở vị trí đồng vị nên suy ra DE // BC
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang
Lại có $\widehat{A
B
C} = {A
C
B}$ (vì tam giác ABC cân tại A) nên BDEC là hình thang cân
Câu 8: Cho hình thang vuông ABCD có $\widehat{A}={B}$ = 90°, AB = AD = 2cm, DC = 4cm. Tính góc ABC của hình thang.
- 135°
- 137°
- 36°
- 136°
 Từ B kẻ BH vuông góc với CD.
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có $\widehat{BHC}$ =
90
°
(do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó $\widehat{B
C
H}$ =
(
180
°
− $\widehat{B C H}$ )
÷
2
=
(
180
°
−
90
°
)
÷
2
=
45
°
Xét hình thang ABCD có:
ˆ
A
B
C
=
360
°
−
( $\widehat{A}$ + $\widehat{D}$ + $\widehat{C}$ )
=
360
°
−
(
90
°
+
90
°
+
45
°
)
=
135
°
Vậy $\widehat{A
B
C}$ =
135
°
.
Câu 9: Một hình thang cân có cạnh bên là 2,5cm; đường trung bình là 3cm. Chu vi của hình thang là:
- 8cm
- 11,5cm
- 12cm
- 11cm
Câu 10: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho DE // BC. Chọn đáp án đúng nhất. Tứ giác BDEC là hình gì?
- Hình thang
- Hình thang cân
- Hình thang vuông
- Cả A, B, C đều sai
Câu 11: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E. Chọn khẳng định đúng nhất?
- Hình thang
- Hình thang vuông
- Hình thang cân
- Cả A, B, C đều sai
Tam giác ADE có AD = AE (gt) nên tam giác ADE cân tại A.
Suy ra $\widehat{A
D
E} = {A
E
D} =
(
180
°
− {D
A
E}$ )
÷
2
(1)
Tam giác ABC cân tại A (gt) nên $\widehat{A
B
C} = {A
C
B} =
(
180
°
− { B
A
C}$ )
÷
2
(2)
Từ (1) và (2) suy ra $\widehat{A
D
E} = {A
B
C}$
Mà 2 góc này là hai góc ở vị trí đồng vị nên suy ra DE // BC
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang
Lại có $\widehat{A
B
C} = {A
C
B}$ (vì tam giác ABC cân tại A) nên BDEC là hình thang cân
Câu 12: Cho hình thang cân MNPQ (MN // PQ) có góc MPQ = 45 độ và hai đáy có độ dài 8cm, 30cm. Diện tích của hình thang cân là:
- $209 cm^2$
- $418 cm^2$
- $290 cm^2$
- $580 cm^2$
Câu 13: Cho hình thang cân MNPQ (MN // PQ) có góc $\widehat{MQP}$ = 45° và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là:
- $728cm^2$
- $364cm^2 $
- $346cm^2 $
- $362cm^2$
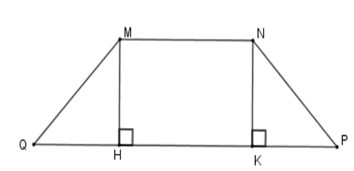
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNKH có MN // HK nên MNKH là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNPK (ch – cgv)
=> QH = KP = $\frac{Q
P
−
H
K}{ 2}$
Mà HK = MN = 12 cm nên QH = KP = $\frac{40
−
12}{ 2}$ = 14 cm
Mà $\widehat{M
Q
P}$ =
45
°
=> ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là $S_{MNPQ} = \frac{(
M
N
+
P
Q
) . M
H }{2}$ = $\frac{(
12
+
40
)
.14}{ 2}$ = $364 cm ^2$
Câu 14: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho DE // BC. Chọn đáp án đúng nhất. Tứ giác BDEC là hình gì?
- Hình thang
- Hình thang vuông
- Hình thang cân
- Cả A, B, C đều sai
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang.
Lại có $\widehat{A
B
C} = {A
C
B}$ (vì tam giác ABC cân tại A) nên BDEC là hình thang cân
Câu 15: Cho hình thang cân ABCD có đáy nhỏ AB = 4cm, đường AH = 6cm, và $\widehat{D}$ = 45° . Độ dài đáy lớn CD bằng
- 12 cm
- 16 cm
- 18 cm
- 20 cm
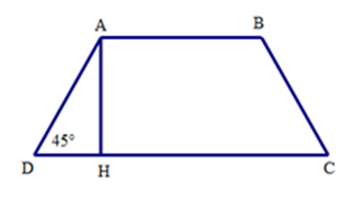 Ta có tam giác ADH vuông cân tại H vì $\widehat{D}$= $45^0$.
Ta có tam giác ADH vuông cân tại H vì $\widehat{D}$= $45^0$.
Do đó DH = AH = 6cm
Mà DH = $\frac{1 }{2} (CD – AB)$
Suy ra CD = 2DH + AB = 12 + 4 = 16 (cm)
Vậy CD = 16 cm.
Câu 16: Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE. Tứ giác BDEC là hình gì ?
- Hình thang
- Hình thang vuông
- Hình thang cân
- Hình chữ nhật
 Ta có: AD = AE
Ta có: AD = AE
⇒ Tam giác ADE cân tại A
⇒ ADE = $90^0$ - DAE/2
mà ABC = $90^0$- BAC/2 (tam giác ABC cân tại A)
⇒ ADE = ABC
mà 2 góc này ở vị trí so le trong
⇒ DE // BC
⇒ BDEC là hình thang
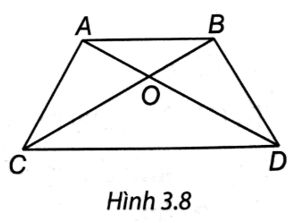
Câu 17: Cho hình thang ABCD có AB // CD , hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD . Tìm khẳng định sai trong các khẳng định sau?
- ABCD là hình thang cân
- AC = BD
- Tam giác AOD cân tại O.
- BC = AD
Ta có: OA = OB; OC = OD suy ra OA + OC = OB + OD
Khi đó AC = BD nên ABCD là hình thang cân. Do đó A, B đúng.
ABCD là hình thang cân nên hai cạnh bên bằng nhau nên BD = AC. Do đó D đúng.
Vì A, O, C thẳng hàng nên C là khẳng định sai.
Câu 18: Cho hình thang cân ABCD (AB // CD, AB < CD ). Kẻ các đường cao AE, BF của hình thang. So sánh DE và CF.
- DE > CF
- DE = CF
- DE < CF
- Không so sánh được
Xét hai tam giác vuông ADE và BCF
Có: AD=BC (hình thang cân ABCD)
góc D = góc C (hình thang cân ABCD)
=> tam giác vuông ADE = Tam giác vuông BCF (cạnh huyền_góc nhọn)
=> DE = CF

0 Comments:
Đăng nhận xét