Bài 1: (1,75 điểm) Phân tích các đa thức sau thành nhân tử :
a) \(3x{y^3} + 6{x^3}y\)
b) \({a^3} + 2{a^2} - 4a - 8\)
c) \(4{x^2} - 4{y^2} + 4x + 1\)
Bài 2: (3,25 điểm) Thực hiện các phép tính :
a) \(\left( {3 - 2a} \right)\left( {a + 1} \right) + a\left( {2a - 1} \right)\)
b) \(\dfrac{{{x^2} + 9}}{{{x^2} + 3x}} + \dfrac{6}{{x + 3}}\) (với \(x \ne 0,\,x \ne - 3\)).
c)\(\dfrac{{2 + x}}{{2 - x}} + \dfrac{{4{x^2}}}{{4 - {x^2}}} + \dfrac{{x - 2}}{{2 + x}}\) (với \(x \ne 2,\) \(x \ne - 2\))
d) \(\left( {{x^3} + 4{x^2} + 6x + 4} \right):\left( {x + 2} \right)\)
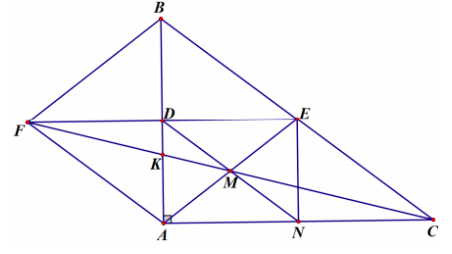
Bài 3: (3,5 điểm) Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 12cm,\,BC = 20cm.\) Gọi \(D\) là trung điểm của \(AB,\) \(E\) là trung điểm của \(BC\).
a) Tính độ dài của \(AC\) và \(DE.\)
b) Gọi \(F\) là điểm đối xứng của \(E\) qua \(D\). Chứng minh tứ giác \(AFEC\) là hình bình hành và tứ giác \(AFBE\) là hình thoi.
c) \(CF\) cắt \(AE\) và \(AB\) lần lượt tại \(M\) và \(K\). \(DM\) cắt \(AC\) tại \(N\). Chứng minh \(\Delta MDF = \Delta MNC\) và tứ giác \(ADEN\) là hình chữ nhật.
d) Tính độ dài của \(BK.\)
Bài 4: (1,0 điểm) Nhân dịp cuối năm, một cửa hàng cần thanh lý một lô hàng (cùng loại sản phẩm) với giá bán là \(2.400.000\) đồng. Lần đầu cửa hàng giảm \(10\% \) so với giá bán thì được \(12\) sản phẩm, lần sau cửa hàng giảm thêm \(5\% \) nữa (so vớ giá đã giảm lần đầu) thì bán được thêm \(20\) sản phẩm.
a) Hỏi sau hai lần giảm giá thì một sản phẩm được bán với giá bao nhiêu tiền ?
b) Sau khi bán hết \(32\) sản phẩm thì cửa hàng lãi được \(9.360.000\) đồng. Hỏi giá vốn của một sản phẩm trong lô hàng cần thanh lý là bao nhiêu tiền ?
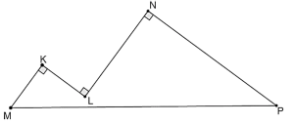
Bài 5: (0,5 điểm) Mặt cắt của một công trình có thiết kế như hình bên, hai dỉnh của công trình là hai góc vuông, hai mái nhà giao nhau tại \(L\) và tạo thành một góc vuông. Biết rằng chều dài các mái lần lượt từ trái sang phải như sau : \(KM = KL = 10m,\) \(LN = 20m,\,NP = 30m.\) Tính chiều dài đoạn \(MP\) trong hình.
HƯỚNG DẪN GIẢI CHI TIẾT
Thực hiện: Ban chuyên môn Loigiaihay.com
Bài 1 (VD):
Phương pháp:
a) Dùng phương pháp đặt nhân tử chung để phân tích thành nhân tử
b) Dùng phương pháp nhóm hạng tử và đặt nhân tử chung để phân tích
c) Dùng hằng đẳng thức \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\) và \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) để phân tích thành nhân tử
Cách giải:
a) \(3x{y^3} + 6{x^3}y\)
\( = 3xy.\left( {{y^2} + 2{x^2}} \right)\)
b) \({a^3} + 2{a^2} - 4a - 8\)
\( = {a^2}\left( {a + 2} \right) - 4\left( {a + 2} \right)\)
\( = \left( {a + 2} \right)\left( {{a^2} - 4} \right)\)
\( = {\left( {a + 2} \right)^2}\left( {a - 2} \right).\)
c) \(4{x^2} - 4{y^2} + 4x + 1\)
\( = \left( {4{x^2} + 4x + 1} \right) - 4{y^2}\)
\( = {\left( {2x + 1} \right)^2} - {\left( {2y} \right)^2}\)
\( = \left( {2x + 1 - 2y} \right)\left( {2x + 1 + 2y} \right)\).
Bài 2 (VD):
Phương pháp:
a) Nhân đa thức với đa thức, nhân đơn thức với đa thức rồi rút gọn
b) Qui đồng mẫu các phân thức rồi cộng các phân thức và rút gọn
c) Qui đồng mẫu các phân thức rồi cộng các phân thức và rút gọn
d) Chia đa thức một biến đã sắp xếp theo hàng dọc hoặc phân tích đa thức bị chia thành nhân tử rồi chia.
Cách giải:
a) \(\left( {3 - 2a} \right)\left( {a + 1} \right) + a\left( {2a - 1} \right)\)
\( = 3a + 3 - 2{a^2} - 2a + 2{a^2} - a\)
\( = 3.\)
b) \(\dfrac{{{x^2} + 9}}{{{x^2} + 3x}} + \dfrac{6}{{x + 3}}\)
\( = \dfrac{{{x^2} + 9}}{{x\left( {x + 3} \right)}} + \dfrac{6}{{x + 3}}\)
\( = \dfrac{{{x^2} + 9 + 6x}}{{x\left( {x + 3} \right)}} = \dfrac{{{{\left( {x + 3} \right)}^2}}}{{x\left( {x + 3} \right)}}\)
\( = \dfrac{{x + 3}}{x}.\)
c) \(\dfrac{{2 + x}}{{2 - x}} + \dfrac{{4{x^2}}}{{4 - {x^2}}} + \dfrac{{x - 2}}{{2 + x}}\)
\( = \dfrac{{{{\left( {2 + x} \right)}^2}}}{{\left( {2 - x} \right)\left( {2 + x} \right)}} + \dfrac{{4{x^2}}}{{\left( {2 - x} \right)\left( {2 + x} \right)}} + \dfrac{{\left( {x - 2} \right)\left( {2 - x} \right)}}{{\left( {2 - x} \right)\left( {2 + x} \right)}}\)
\( = \dfrac{{4 + 4x + {x^2}}}{{\left( {2 - x} \right)\left( {2 + x} \right)}} + \dfrac{{4{x^2}}}{{\left( {2 - x} \right)\left( {2 + x} \right)}} + \dfrac{{2x - {x^2} - 4 + 2x}}{{\left( {2 - x} \right)\left( {2 + x} \right)}}\)
\( = \dfrac{{4 + 4x + {x^2} + 4{x^2} + 2x - {x^2} - 4 + 2x}}{{\left( {2 - x} \right)\left( {2 + x} \right)}}\)
\( = \dfrac{{4{x^2} + 8x}}{{\left( {2 - x} \right)\left( {2 + x} \right)}}\)
\( = \dfrac{{4x\left( {x + 2} \right)}}{{\left( {2 - x} \right)\left( {2 + x} \right)}}\) \( = \dfrac{{4x}}{{2 - x}} \cdot \)
d) \(\left( {{x^3} + 4{x^2} + 6x + 4} \right):\left( {x + 2} \right)\)
\(\begin{array}{l}\left( {{x^3} + 4{x^2} + 6x + 4} \right):\left( {x + 2} \right)\\ = \left( {{x^3} + 2{x^2} + 2{x^2} + 4x + 2x + 4} \right)\\ = \left[ {{x^2}\left( {x + 2} \right) + 2x\left( {x + 2} \right) + 2\left( {x + 2} \right)} \right]:\left( {x + 2} \right)\\ = \left[ {\left( {x + 2} \right)\left( {{x^2} + 2x + 2} \right)} \right]:\left( {x + 2} \right)\\ = {x^2} + 2x + 2\end{array}\)
Bài 3 (VD ):
Phương pháp:
a) Sử dụng định lý Pytago và tính chất đường trung bình trong tam giác
b) Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành
Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường là hình bình hành
Hình bình hành có hai đường chéo vuông góc là hình thoi
c) Chứng minh hai tam giác bằng nhau theo trường hợp góc-cạnh-góc
Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành
Hình bình hành có 1 góc vuông là hình chữ nhật
d) Tính \(AK\) dựa vào tính chất trọng tâm tam giác
Từ đó tính \(BK.\)
Cách giải:
a) Tính độ dài của \(AC\) và \(DE.\)
Xét tam giác \(ABC\) vuông tại \(A,\) áp dụng định lý Py-ta-go :
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow A{C^2} = B{C^2} - A{B^2}\) \( = {20^2} - {12^2} = 256\)
Suy ra \(AC = 16\left( {cm} \right)\)
Vì \(D,E\) lần lượt là trung điểm của \(AB\) và \(BC\) nên \(DE\) là đường trung bình của tam giác \(ABC\)
Suy ra \(DE = \dfrac{1}{2}AC = \dfrac{{16}}{2} = 8\left( {cm} \right)\)
b) Gọi \(F\) là điểm đối xứng của \(E\) qua \(D\). Chứng minh tứ giác \(AFEC\) là hình bình hành và tứ giác \(AFBE\) là hình thoi.
+) Vì \(F\) đối xứng với \(E\) qua \(D\) nên \(D\) là trung điểm của \(EF\) suy ra \(EF = 2.DE\)
Mà \(AC = 2DE\) (cmt) nên \(EF = AC\,\,\left( 1 \right)\)
Lại có \(DE//AC\) (cmt) nên \(EF//AC\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra tứ giác \(AFEC\) là hình bình hành (tứ giác có hai cạnh đối song song và bằng nhau).
+) Vì \(EF//AC\left( {cmt} \right)\) mà \(AB \bot AC \Rightarrow EF \bot AB\)
Xét tứ giác \(AFBE\) có \(EF\) và \(AB\) là hai đường chéo cắt nhau tại trung điểm \(D\) của mỗi đường, suy ra tứ giác\(AFBE\) là hình bình hành.
Mà \(EF\) vuông góc với \(AB\) (cmt)
Nên tứ giác \(AFBE\) là hình thoi (hình bình hành có hai đường chéo vuông góc).
c) \(CF\) cắt \(AE\) và \(AB\) lần lượt tại \(M\) và \(K\). \(DM\) cắt \(AC\) tại \(N\). Chứng minh \(\Delta MDF = \Delta MNC\) và tứ giác \(ADEN\) là hình chữ nhật.
Theo câu b) ta có \(AFEC\) là hình bình hành nên \(M\) là trung điểm của hai đường chéo \(FC,AE.\)
Hay \(MF = MC\)
Xét hai tam giác \(MDF\) và \(MNC\) có:
+) \(\widehat {FMD} = \widehat {CMN}\) (đối đỉnh)
+) \(MF = MC\) (cmt)
+) \(\widehat {DFM} = \widehat {NCM}\) (hai góc ở vị trí so le trong)
Nên \(\Delta MDF = \Delta MNC\) theo trường hợp góc – cạnh – góc
Suy ra \(NC = FD = \dfrac{1}{2}EF = \dfrac{1}{2}AC.\) Do đó \(N\) là trung điểm của \(AC.\)
Xét tứ giác \(DENA\) có: \(DE\) song song với \(AN\) (do \(DE//AC\)) và \(DE = AN = \dfrac{1}{2}AC\) nên tứ giác \(DENA\) là hình bình hành (tứ giác có hai cạnh đối song song và bằng nhau).
Mà \(\widehat {DAN} = 90^\circ \left( {gt} \right)\)
Suy ra tứ giác \(ADEN\) là hình chữ nhật (hình bình hành có một góc vuông).
d) Tính độ dài của \(BK.\)
Xét tam giác \(AFE\) có hai đường trung tuyến \(AD\) và \(FM\) giao nhau tại \(K\) nên \(K\) là trọng tâm của tam giác \(AFE.\)
Nên \(AK = \dfrac{2}{3}AD = \dfrac{2}{3} \cdot \left( {\dfrac{1}{2}AB} \right) = \dfrac{1}{3}AB\)
Suy ra \(BK = AB - AK = AB - \dfrac{1}{3}AB = \dfrac{2}{3}AB = \dfrac{2}{3} \cdot 12 = 8\left( {cm} \right)\)
Bài 4 (VD ):
Phương pháp:
a) Tính giá tiền 1 sản phẩm sau lần giảm giá thứ nhất rồi tính giá tiền 1 sản phẩm sau lần giảm giá thứ hai
b) Tính số tiền thực tế cửa hàng thu được khi bán hết \(32\) sản phẩm, tứ đó tính giá vốn 1 sản phẩm.
Cách giải:
a) Hỏi sau hai lần giảm giá thì một sản phẩm được bán với giá bao nhiêu tiền ?
Giá tiền một sản phẩm sau lần giảm giá đầu :
\(2400000.\left( {1 - 10\% } \right) = 2160000\) (đồng)
Giá tiền một sản phẩm sau lần giảm giá thứ hai :
\(2160000.\left( {1 - 5\% } \right) = 2052000\) (đồng)
b) Sau khi bán hết \(32\) sản phẩm thì cửa hàng lãi được \(9.360.000\) đồng. Hỏi giá vốn của một sản phẩm trong lô hàng cần thanh lý là bao nhiêu tiền ?
Số tiền thực tế cửa hàng thu được khi bán hết \(32\) sản phẩm :
\(2160000.12 + 2052000.20 = 66960000\) (đồng)
Giá vốn của một sản phẩm :
\(\left( {66960000 - 9360000} \right):32 = 1800000\) (đồng)
Bài 5 (VD ):
Phương pháp:
Kéo dài tia \(MK\) cắt tia \(PN\) tại \(Q.\)
Sử dụng định lý Pytago trong tam giác vuông \(MPQ\) để tính \(MP.\)
Cách giải:
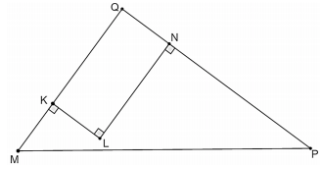
Kéo dài tia \(MK\) cắt tia \(PN\) tại \(Q.\)
Tứ giác \(KLNQ\) có \(\widehat K = \widehat L = \widehat N\) nên \(KLNQ\) là hình chữ nhật, do đó \(\widehat {KQN} = 90^\circ ,\) \(QN = KL = 10\left( m \right),\) \(QK = NL = 20\left( m \right).\)
Từ đó ta có:
\(\begin{array}{l}QM = KQ + KM = 20 + 10 = 30\left( m \right),\\\,QP = QN + NP = 10 + 30 = 40\left( m \right)\end{array}\)
Áp dụng định lý Py-ta-go trong tam giác vuông \(QMP,\) ta có:
\(M{P^2} = M{Q^2} + Q{P^2} = {30^2} + {40^2} = 2500\) nên \(MP = 50\left( m \right).\)
Loigiaihay.com

0 Comments:
Đăng nhận xét