Câu 1 (2,5 điểm) :
a) Phân tích đa thức sau thành nhân tử \({x^2} - 6x + 2\left( {x - 6} \right).\)
b) Tính và rút gọn : \(\dfrac{6}{{x - 2}} - \dfrac{{12}}{{x\left( {x - 2} \right)}} - \dfrac{7}{x}\)
c) Tìm \(x\) biết : \(10x + 8 - 4x\left( {5x + 4} \right) = 0\)
Câu 2 (1 điểm) : Một phòng học có kích thước dài \(10m,\) rộng \(6m.\) Người ta lát nền bằng gạch có hình vuông cạnh dài \(50cm.\) Tính số tiền mua gạch để lát nền lớp học đó biết một thùng gạch giá \(120\,000\) đồng. (\(1\) thùng có \(8\) viên gạch)
Câu 3 (1 điểm) : Mức đóng bảo hiểm y tế của các thành viên thuộc hộ gia đình theo Luật Bảo hiểm y tế được tính như sau : Người thứ nhất đóng bằng \(4,5\% \) mức lương cơ sở của người đó; người thứ hai đóng bằng \(70\% \) mức đóng của người thứ nhất. Hiện tại, người thứ nhất có mức lương cơ sở là \(14\,520\,000\) đồng một năm. Hỏi người thứ hai trong gia đình sẽ đóng bảo hiểm y tế là bao nhiêu tiền một năm ?
Câu 4 (1 điểm) : Bạn Việt muốn tính độ dài \(BC\) của một hồ bơi nhưng bạn chỉ đo được độ dài đoạn \(MN = 2m,\) biết \(M\) và \(N\) lần lượt là trung điểm của \(AC\) và \(AB.\) Bạn hãy tính độ dài \(BC\) dùm bạn Việt?

Câu 5 (1 điểm) : Một tủ kệ trang trí hình tam giác đều có chu vi là \(180cm,\) gồm \(2\) tam giác đều nhỏ và \(1\) hình thoi bên trong (như hình bên). Tính chu vi hình thoi ?

Câu 6 (3,5 điểm) : Cho tam giác \(ABC\) cân tại \(A.\) Gọi \(M,N,H\) theo thứ tự là trung điểm của \(AB,AC\) và \(BC.\)
a) Tứ giác \(BMNC\) và tứ giác \(BMNH\) là hình gì? Vì sao?
b) Gọi \(D\) là điểm đối xứng với \(H\) qua \(N.\) Chứng minh: \(ADCH\) là hình chữ nhật
c) Kẻ \(DE \bot AC,\) gọi \(K\) là trung điểm của \(EC.\) Qua \(K\) vẽ đường thẳng \(d \bot DK.\) Chứng minh: Ba đường thẳng \(AH,MN\) và \(d\) đồng qui (cùng gặp nhau tại 1 điểm)
HƯỚNG DẪN GIẢI CHI TIẾT
Thực hiện: Ban chuyên môn Loigiaihay.com
Câu 1 (VD):
Phương pháp:
a) Sử dụng phương pháp nhóm hạng tử và đặt nhân tử chung để phân tích
b) Qui đồng mẫu các phân thức và rút gọn
c) Phân tích vế trái để đưa về dạng \(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)
Cách giải:
a) Phân tích đa thức sau thành nhân tử \({x^2} - 6x + 2\left( {x - 6} \right).\)
Ta có:
\(\begin{array}{l}{x^2} - 6x + 2\left( {x - 6} \right)\\ = x\left( {x - 6} \right) + 2\left( {x - 6} \right)\\ = \left( {x + 2} \right)\left( {x - 6} \right)\end{array}\)
b) Tính và rút gọn : \(\dfrac{6}{{x - 2}} - \dfrac{{12}}{{x\left( {x - 2} \right)}} - \dfrac{7}{x}\)
Điều kiện: \(x \ne \left\{ {0;2} \right\}\)
Ta có:
\(\begin{array}{l}\dfrac{6}{{x - 2}} - \dfrac{{12}}{{x\left( {x - 2} \right)}} - \dfrac{7}{x}\\ = \dfrac{{6x}}{{x\left( {x - 2} \right)}} - \dfrac{{12}}{{x\left( {x - 2} \right)}} - \dfrac{{7\left( {x - 2} \right)}}{{x\left( {x - 2} \right)}}\\ = \dfrac{{6x - 12 - 7x + 14}}{{x\left( {x - 2} \right)}}\\ = \dfrac{{ - x + 2}}{{x\left( {x - 2} \right)}}\\ = \dfrac{{ - \left( {x - 2} \right)}}{{x\left( {x - 2} \right)}} = - \dfrac{1}{x}\end{array}\)
c) Tìm \(x\) biết : \(10x + 8 - 4x\left( {5x + 4} \right) = 0\)
Ta có:
\(\begin{array}{l}10x + 8 - 4x\left( {5x + 4} \right) = 0\\ \Leftrightarrow 2\left( {5x + 4} \right) - 4x\left( {5x + 4} \right) = 0\\ \Leftrightarrow \left( {2 - 4x} \right)\left( {5x + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2 - 4x = 0\\5x + 4 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}4x = 2\\5x = - 4\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\\x = - \dfrac{4}{5}\end{array} \right.\end{array}\)
Vậy \(x = \dfrac{1}{2};x = - \dfrac{4}{5}\)
Câu 2 (VD):
Phương pháp:
Tính diện tích phòng học
Tính diện tích 1 viên gạch
Tính số viên gạch cần dùng
Tính giá tiền 1 viên gạch
Tính số tiền mua gạch
Cách giải:
Diện tích phòng học là: \(10.6 = 60{m^2}\)
Đổi \(50cm = 0,5m\)
Diện tích 1 viên gạch là \(0,5.0,5 = 0,25{m^2}\)
Số gạch cần dùng để lát nền là: \(60:0,25 = 240\) viên
Giá tiền 1 viên gạch là: \(120000:8 = 15000\) đồng
Số tiền mua gạch là: \(240.15000 = 3600000\) đồng.
Câu 3 (VD):
Phương pháp:
Tính mức đóng bảo hiểm y tế của người thứ nhất
Tính mức đóng bảo hiểm y tế của người thứ hai trong gia đình
Cách giải:
Mức đóng bảo hiểm y tế của người thứ nhất là: \(14520000.4,5\% = 653400\) đồng/1 năm
Mức đóng bảo hiểm y tế của người thứ hai là: \(653400.70\% = 457380\) đồng/1 năm
Câu 4 (VD):
Phương pháp:
Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
Cách giải:
Xét tam giác \(ABC\) có \(MN\) là đường trung bình nên \(MN = \dfrac{1}{2}BC \Rightarrow BC = 2MN = 2.2 = 4m\)
Vậy \(BC = 4m.\)
Câu 5 (VD):
Phương pháp:
Chu vi hình thoi bằng cạnh nhân 4
Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
Cách giải:
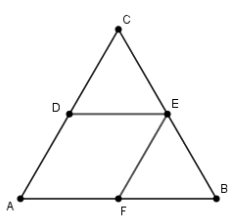
Ta đưa về bài toán: Cho tam giác \(ABC\) đều có chu vi \(180cm,\) các tam giác \(CED,BEF\) là các tam giác đều, \(DEFA\) là hình thoi. Tính chu vi hình thoi \(ADEF\).
Giải: Vì các tam giác \(CED,BEF\) là các tam giác đều nên \(CD = CE = DE = CF = EB = FB\)
Lại có \(ADEF\) là hình thoi nên \(CD = CE = DE = CF = EB = FB = AF = AD\)
Hay \(D,E,F\) lần lượt là trung điểm cạnh \(AC,BC,AB.\)
Suy ra \(AD = \dfrac{{AC}}{2}\)
Lại có \(AB + AC + BC = 180 \Leftrightarrow 3AC = 180\) \( \Rightarrow AC = 60cm\)
Nên \(AD = \dfrac{{AC}}{2} = \dfrac{{60}}{2} = 30cm\)
Chu vi hình thoi \(ADEF\) là \(30.4 = 120cm.\)
Câu 6 (VD):
Phương pháp:
a) Sử dụng: Tứ giác có hai cạnh đối song song là hình thang
Hình thang có hai góc ở đáy bằng nhau là hình thang cân
Tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành
b) Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường là hình bình hành
Hình bình hành có 1 góc vuông là hình chữ nhật
c) Lấy \(P\) là trung điểm cạnh \(EP.\) Gọi \(I\) là giao điểm của \(MN\) và \(AH.\) Ta sẽ chứng minh \(IK \bot DK\)
Chỉ ra \(IAPK\) là hình bình hành, \(P\) là trực tâm tam giác \(ADK.\) Từ đó sử dụng quan hệ từ vuông góc đến song sông để chứng minh \(IK \bot DK\).
Cách giải:
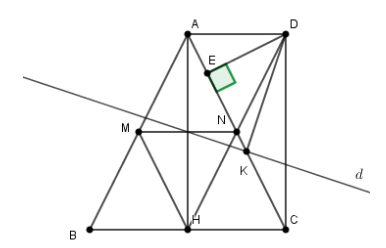
a) Tứ giác \(BMNC\) và tứ giác \(BMNH\) là hình gì? Vì sao?
Xét tam giác \(ABC\) có \(MN\) là đường trung bình của tam giác nên \(MN//BC,\,MN = \dfrac{{BC}}{2} = BH\)
Suy ra \(MNCB\) là hình thang. Lại có \(\widehat B = \widehat C\) nên \(MNCB\) là hình thang cân (dhnb)
Xét tứ giác \(MNHB\) có \(MN//HB;MN = HB\) nên \(MNHB\) là hình bình hành (dhnb)
b) Gọi \(D\) là điểm đối xứng với \(H\) qua \(N.\) Chứng minh: \(ADCH\) là hình chữ nhật
Xét tứ giác \(AHCD\) có \(N\) là trung điểm \(AC\left( {gt} \right)\) và \(N\) là trung điểm \(HD\) (do \(D\) đối xứng với \(H\) qua \(N\))
Nên hai đường chéo \(AC,HD\) giao nhau tại trung điểm mỗi đường.
Suy ra \(AHCD\) là hình bình hành
Lại có \(\Delta ABC\) cân tại \(A\) có \(AH\) là đường trung tuyến nên \(AH\) cũng là đường cao.
Suy ra \(AH \bot HC \Rightarrow \widehat {AHC} = {90^0}\)
Từ đó \(AHCD\) là hình chữ nhật (dhnb)
c) Kẻ \(DE \bot AC,\) gọi \(K\) là trung điểm của \(EC.\) Qua \(K\) vẽ đường thẳng \(d \bot DK.\) Chứng minh: Ba đường thẳng \(AH,MN\) và \(d\) đồng qui (cùng gặp nhau tại 1 điểm)
(fb: Thầy Lê Minh Đức)
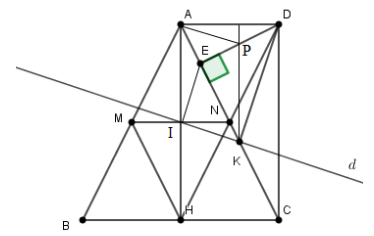
Lấy \(P\) là trung điểm cạnh \(EP.\) Gọi \(I\) là giao điểm của \(MN\) và \(AH.\) Ta sẽ chứng minh \(IK \bot DK\)
Xét tam giác \(AHC\) có \(IN//HC\) và \(N\) là trung điểm \(AC\) nên \(I\) là trung điểm của \(AH\)
Suy ra \(AI = \dfrac{{AH}}{2}\) và \(AI//DC;AH = DC\) (do \(ADCH\) là hình chữ nhật) nên \(AI = \dfrac{{DC}}{2}\)
Xét tam giác \(EPC\) có \(PK\) là đường trung bình của tam giác \( \Rightarrow PK//DC,PK = \dfrac{1}{2}DC\)
Xét tứ giác \(AIPK\) có \(AI = PK\left( { = \dfrac{{DC}}{2}} \right);AI//PK//DC\) nên \(AIPK\) là hình bình hành.
Do đó: \(IK//AP\)
Lại có \(PK//DC\) mà \(DC \bot AD \Rightarrow PK \bot AD\)
Từ đó suy ra \(P\) là trực tâm tam giác \(ADK.\)
Suy ra \(AP \bot DK\) mà \(IK//AP\) nên \(IK \bot DK\)
Do đó \(IK \equiv d\) nên ba đường thẳng \(AH,MN,d\) đồng qui tại điểm \(I\) (đpcm)
Loigiaihay.com

0 Comments:
Đăng nhận xét