Giải bài tập Toán lớp 8 Bài 3: Tính chất đường phân giác của tam giác

 

Giải Toán 8 trang 55 Tập 2

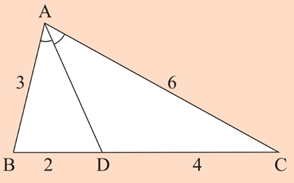
Khởi động trang 55 Toán 8 Tập 2: Đường phân giác AD của tam giác ABC chia cạnh đối diện BC thành hai đoạn tỉ lệ với hai đoạn thẳng nào trong hình?

Lời giải:

Dựa vào độ dài các cạnh ở trên hình vẽ, ta có:

$\frac{AB}{AC}=\frac{3}{6}=\frac{1}{2};\frac{BD}{CD}=\frac{2}{4}=\frac{1}{2}$

Do đó, đường phân giác AD của tam giác ABC chia cạnh đối diện BC thành hai đoạn BD. CD tỉ lệ với hai đoạn thẳng AB, AC trong hình.

1. Tính chất đường phân giác của tam giác

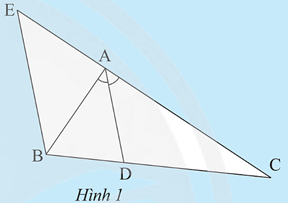
Khám phá trang 55 Toán 8 Tập 2: Cho tam giác ABC có đường phân giác AD. Vẽ đường thẳng qua B song song với AD và cắt đường thẳng AC tại E (Hình 1). Hãy giải thích tại sao:

a) Tam giác BAE cân tại A.

b) $\frac{DB}{DC}=\frac{AE}{AC}=\frac{AB}{AC}$.

Lời giải:

a) Ta có: BE // AD suy ra $\widehat{AEB}=\widehat{CAD}$ (hai góc đồng vị), $\widehat{ABE}=\widehat{BAD}$ (hai góc so le trong)

AD là tia phân giác góc $\widehat{BAC}$ nên $\widehat{BAD}=\widehat{CAD}$

Do đó: $\widehat{AEB}=\widehat{ABE}$ suy ra tam giác BAE cân tại A

b) Xét tam giác BCE có AD // BE, theo định lí Thalès, ta có:

$\frac{DB}{DC}=\frac{AE}{AC}$

Mà AE = AB (do tam giác ABE cân tại A)

Do đó: $\frac{DB}{DC}=\frac{AE}{AC}=\frac{AB}{AC}$

2. Áp dụng tính chia tỉ lệ của đường phân giác của tam giác

Giải Toán 8 trang 56 Tập 2

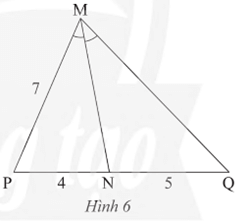
Thực hành trang 56 Toán 8 Tập 2: Tính độ dài cạnh MQ của tam giác MPQ trong Hình 6.

Lời giải:

Trong tam giác MPQ, ta có MN là đường phân giác góc M nên ta có

$\frac{NP}{NQ}=\frac{MP}{MQ}$ hay $\frac{4}{5}=\frac{7}{MQ}$

Do đó $\mathrm{MQ}=\frac{7.5}{4}=8,75$

Bài tập

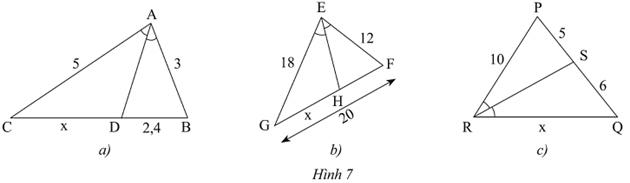
Bài 1 trang 56 Toán 8 Tập 2: Tính độ dài x trong Hình 7.

Lời giải:

a) Trong tam giác ABC, ta có AD là đường phân giác góc A nên ta có

$\frac{DC}{DB}=\frac{AC}{AB}$ hay $\frac{x}{2,4}=\frac{5}{3}$

Suy ra $x=\frac{5.2,4}{3}=4$

b) Trong tam giác EFG, ta có EH là đường phân giác góc E nên ta có

$\frac{HG}{HF}=\frac{EG}{EF}$ hay $\frac{x}{20-x}=\frac{18}{12}$

Suy ra $12x=18(20-x)\Rightarrow x=\frac{18.20}{30}=12$

c) Trong tam giác PQR, ta có RS là đường phân giác góc R nên ta có

$\frac{SP}{SQ}=\frac{PR}{QR}$ hay $\frac{5}{6}=\frac{10}{x}$.

Suy ra $x=\frac{6.10}{5}=12$

Giải Toán 8 trang 57 Tập 2

Bài 2 trang 57 Toán 8 Tập 2: Tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Đường phân giác của góc BAC cắt cạnh BC tại D.

a) Tính độ dài các đoạn thẳng DB và DC.

b) Tính tỉ số diện tích giữa ΔADB và ΔADC.

Lời giải:

a) Tam giác ABC có AD là đường phân giác nên $\frac{DB}{AB}=\frac{DC}{AC}$

Áp dụng tính chất dãy tỉ số bằng nhau, ta có

$\frac{DB}{AB}=\frac{DC}{AC}=\frac{DB+DC}{AB+AC}=\frac{BC}{AB+AC}$

Nên $\frac{DB}{8}=\frac{DC}{6}=\frac{10}{8+6}$

Vậy $\mathrm{DB}=\frac{40}{7}\mathrm{cm},\mathrm{BC}=\frac{30}{7}\mathrm{cm}$

b) Vẽ AH ⊥ BC tại H

$\frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH.DB}{\frac{1}{2}AH.DC}=\frac{DB}{DC}=\frac{\frac{40}{7}}{\frac{30}{7}}=\frac{4}{3}$.

Bài 3 trang 57 Toán 8 Tập 2: Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt BC tại D. Qua D vẽ DE // AB (E ∈ AC).

a) Tính độ dài các đoạn thẳng DB, DC và DE.

b) Chứng minh ABC là tam giác vuông. Tính diện tích tam giác ABC.

c) Tính diện tích các tam giác ADB, ADE và DCE.

Lời giải:

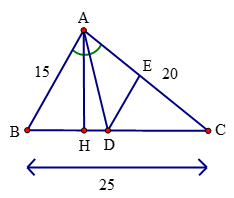
a) Trong tam giác ABC, ta có: AD là tia phân giác của $\widehat{BAC}$.

Suy ra: $\frac{DB}{DC}=\frac{AB}{AC}$(tính chất đường phân giác)

Mà AB = 15 cm; AC = 20 cm.

Nên $\frac{DB}{Dc}=\frac{15}{20}$

Suy ra: $\frac{DB}{DB+DC}=\frac{15}{15+20}$ (tính chất tỉ lệ thức)

Suy ra: $\frac{DB}{BC}=\frac{15}{35}$

Nên: $\mathrm{DB}=\frac{15}{35}.25=\frac{75}{7}\left(\mathrm{cm}\right)$

Do đó $DC=BC-BD=25-\frac{75}{7}=\frac{100}{7}\left(\mathrm{cm}\right)$

Xét tam giác ABC có DE // AB, theo hệ quả định lí Thalès, ta có:

$\frac{DE}{AB}=\frac{CD}{BC}\Rightarrow \frac{DE}{15}=\frac{\frac{100}{7}}{25}$

Vậy $\mathrm{DE}=\frac{60}{7}\mathrm{cm}$.

b) Xét tam giác ABC ta có: AB = 15 cm, AC = 20 cm, BC = 25 cm.

Nên ${\mathrm{BC}}^2=A{B}^2+A{C}^2$ suy ra tam giác ABC vuông tại A.

Khi đó, ta có: $S_{ABC}=\frac{1}{2}AC.AB=\frac{1}{2}.20.15=150\left(c{m}^2\right)$

Vậy diện tích tam giác ABC là 150 cm2.

c) Kẻ AH ⊥ BC ta có: 

$\frac{S_{ADB}}{S_{ABC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.BC}=\frac{DB}{DC}=\frac{\frac{40}{7}}{\frac{30}{7}}=\frac{4}{3}$

Suy ra $S_{ADB}=\frac{3}{7}\cdot S_{ABC}=\frac{3}{7}\cdot 150=\frac{450}{7}\left(c{m}^2\right)$

$\frac{S_{DCE}}{S_{ABC}}=\frac{\frac{1}{2}CE.DE}{\frac{1}{2}AC.AB}={\left(\frac{DE}{AB}\right)}^2={\left(\frac{\frac{60}{7}}{25}\right)}^2=\frac{144}{1225}$

Suy ra

$S_{DCE}=\frac{144}{1225}\cdot S_{ABC}=\frac{144}{1225}\cdot 150=\frac{864}{49}\left(c{m}^2\right)$

$S_{ADE}=S_{ABC}-S_{ADB}-S_{DCE}=150-\frac{450}{7}-\frac{864}{49}=\frac{3336}{49}\left(c{m}^2\right)$

Vậy $S_{ADB}=\frac{450}{7}c{m}^2;S_{DCE}=\frac{864}{49}c{m}^2;S_{ADE}=\frac{3336}{49}c{m}^2$

Bài 4 trang 57 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Đường phân giác của góc A cắt BC tại D.

a) Tính BC, DB, DC.

b) Vẽ đường cao AH. Tính AH, HD và AD.

Lời giải:

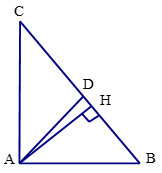
a) Tam giác ABC vuông tại A, áp dụng định lí Pythagore, ta có: 

$B{C}^2=A{C}^2+A{B}^2$ suy ra BC = 5 cm

AD là tia phân giác góc A nên $\frac{DB}{DC}=\frac{AB}{AC}$ suy ra $\frac{DB}{5-DB}=\frac{3}{4}$

$\Rightarrow 4DB=15-3DB\Rightarrow DB=\frac{15}{7}\left(cm\right).$

Do đó $DC=BC-DB=5-\frac{15}{7}=\frac{20}{7}\left(cm\right).$

Vậy BC = 5 cm, $DB=\frac{15}{7}\mathrm{cm}$, $DC=\frac{20}{7}\mathrm{cm}$

b) Ta có: $S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}AH.BC$

$\Rightarrow AH=\frac{AB.AC}{BC}=\frac{3.4}{5}=\frac{12}{5}\left(\mathrm{cm}\right)$

Tam giác ABH vuông tại H nên 

$HB=\sqrt{A{B}^2-A{H}^2}=\sqrt{3^2-{\left(\frac{12}{5}\right)}^2}=\frac{9}{5}\left(\mathrm{cm}\right)$

Ta có: $HD=DB-HB=\frac{15}{7}-\frac{9}{5}=\frac{12}{35}$(cm)

Tam giác ABH vuông tại H nên 

$AD=\sqrt{H{D}^2+A{H}^2}=\sqrt{{\left(\frac{12}{35}\right)}^2+{\left(\frac{12}{5}\right)}^2}=\frac{12\sqrt{2}}{7}\left(cm\right)$

Vậy $AH=\frac{12}{5}\mathrm{cm}$, $\mathrm{HD}=\frac{12}{35}\mathrm{cm}$, $AD=\frac{12\sqrt{2}}{7}\mathrm{cm}$.

Bài 5 trang 57 Toán 8 Tập 2: Cho tam giác ABC có trung tuyến AM. Đường phân giác của góc AMB cắt AB tại D và đường phân giác của góc AMC cắt AC tại E (Hình 8). Chứng minh DE // BC.

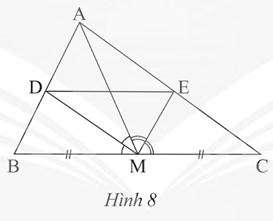
Lời giải:

• Xét tam giác ABM có MD là đường phân giác $\widehat{AMB}$ suy ra $\frac{DA}{DB}=\frac{MA}{MB}$.

• Xét tam giác ACM có ME là đường phân giác $\widehat{AMC}$ suy ra $\frac{EA}{\mathrm{EB}}=\frac{MA}{MC}$.

Mà MB = MC, do đó: $\frac{DA}{DB}=\frac{EA}{EC}$, theo định lí Thalès đảo ta có: DE // BC.