Giải bài tập Toán lớp 8 Bài 2: Đường trung bình của tam giác

Giải Toán 8 trang 52 Tập 2

Khởi động trang 52 Toán 8 Tập 2: Giữa hai điểm B và C có một hồ nước (xem hình bên). Biết DE = 45 m. Làm thế nào để tính được khoảng cách giữa hai điểm B và C?

Lời giải:

Xét tam giác ABC, ta có: 

$\frac{AD}{\mathrm{AB}}=\frac{AE}{AC}=\frac{1}{2}$

Theo định lí Thalès đảo, ta có DE // BC.

Suy ra $\frac{DE}{BC}=\frac{AD}{AB}=\frac{1}{2}$, vậy BC = 2DE = 90 m.

Sau khi học xong bài này:

Ta có: D, E là trung điểm của AB và AC nên DE là đường trung bình của tam giác ABC

suy ra $DE=\frac{1}{2}BC$ vậy BC = 2DE = 90 m.

1. Đường trung bình của tam giác

Khám phá 1 trang 52 Toán 8 Tập 2: Cho tam giác ABC, vẽ đường thẳng d đi qua trung điểm M của cạnh AB, song song với cạnh BC và cắt AC tại N (Hình 1). Hãy chứng minh N là trung điểm của AC.

Lời giải:

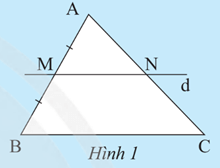
Xét tam giác ABC có MN // BC, theo định lí Thalès, ta có:

$\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{2}$

Suy ra N là trung điểm của AC.

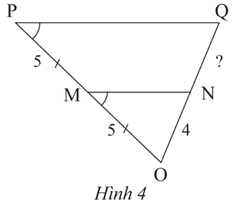
Thực hành 1 trang 52 Toán 8 Tập 2: Tìm độ dài đoạn thẳng NQ trong Hình 4.

Lời giải:

Ta có: $\widehat{OPQ}=\widehat{OMN}$ mà hai góc này ở vị trí đồng vị nên MN // PQ.

Xét tam giác OPQ ta có:

MN // PQ

M là trung điểm OP

Suy ra MN là đường trung bình tam giác OPQ.

Do đó là trung điểm OQ ⇒ NQ = ON = 4.

Giải Toán 8 trang 53 Tập 2

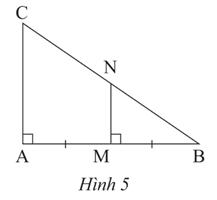
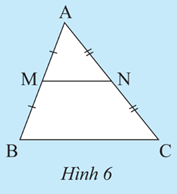
Vận dụng 1 trang 53 Toán 8 Tập 2: Trong Hình 5, chứng minh MN là đường trung bình của tam giác ABC.

Lời giải:

Ta có: MN ⊥ AB, AC ⊥ AB nên MN // AC.

Xét tam giác ABC có:

MN // AC

M là trung điểm AB

Suy ra MN là đường trung bình tam giác ABC.

2. Tính chất của đường trung bình

Khám phá 2 trang 53 Toán 8 Tập 2: Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC.

a) Tính các tỉ số $\frac{AM}{AB},\frac{AN}{AC}$;

b) Chứng minh MN // BC;

c) Chứng minh $\frac{MN}{BC}=\frac{1}{2}$

Lời giải:

a) Vì M là trung điểm AB suy ra $\frac{AM}{AB}=\frac{1}{2}$

Tương tự, $\frac{AN}{AC}=\frac{1}{2}$

b) Xét tam giác ABC có $\frac{AM}{AB}=\frac{AN}{AC}$

Theo định lí Thalès đảo, ta có: MN // BC.

c) Xét tam giác ABC có MN // BC.

Áp dụng hệ quả định lí Thalès, ta có:

$\frac{MN}{BC}=\frac{AM}{AB}=\frac{1}{2}$

Thực hành 2 trang 53 Toán 8 Tập 2: Trong Hình 8, cho biết JK = 10 cm, DE = 6,5 cm, EL = 3,7 cm. Tính DJ, EF, DF, KL.

Lời giải:

D là trung điểm của JK suy ra $DJ=\frac{1}{2}JK=\frac{1}{2}.10=5\left(\mathrm{cm}\right)$

E là trung điểm của JL suy ra JL = 2EL = 2.3,7 = 7,4 (cm)

Trong tam giác JKL có:

D là trung điểm của JK

E là trung điểm của JL

Suy ra DE là đường trung bình của tam giác JKL.

Do đó KL = 2DE = 2.6,5 = 13 (cm).

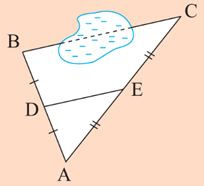
Vận dụng 2 trang 53 Toán 8 Tập 2: Hãy tính khoảng cách BC trong phần Hoạt động khởi động (trang 52).

Lời giải:

Xét tam giác ABC ta có: 

$\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{2}$

Theo định lí Thalès đảo ta có DE // BC.

Suy ra $\frac{DE}{\mathrm{BC}}=\frac{AD}{AB}=\frac{1}{2}$, vậy BC = 2DE = 90 m.

Ta có: D là trung điểm của AB

           E là trung điểm của AC

Suy ra DE là đường trung bình của tam giác ABC.

⇒$DE=\frac{1}{2}BC$

Vậy BC = 2DE = 90 m.

Bài tập

Bài 1 trang 53 Toán 8 Tập 2: Cho MN là đường trung bình của mỗi tam giác ABC trong Hình 9. Hãy tìm giá trị x trong mỗi hình.

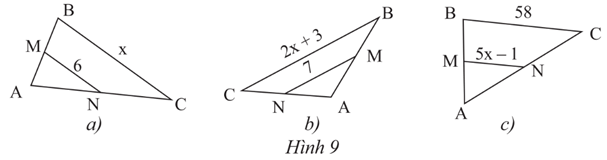
Lời giải:

a) Xét tam giác ABC có MN là đường trung bình ta có:

BC = 2MN

x = 12.

b) Xét tam giác ABC có MN là đường trung bình ta có:

BC = 2MN

2x + 3 = 14

x = 112.

c) Xét tam giác ABC có MN là đường trung bình ta có:

BC = 2MN

58 = 2(5x − 1)

58 = 10x – 2

x = 6

Giải Toán 8 trang 54 Tập 2

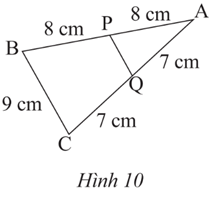
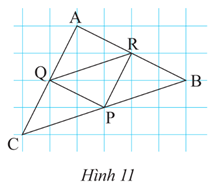
Bài 2 trang 54 Toán 8 Tập 2: Tính độ dài đoạn PQ (Hình 10).

Lời giải:

Xét tam giác ABC có:

AP = PB = 8 cm

AQ = QC = 7 cm

Khi đó, PQ là đường trung bình tam giác ABC.

Do đó $PQ=\frac{1}{2}BC=\frac{1}{2}.9=4,5$ (cm).

Bài 3 trang 54 Toán 8 Tập 2: Cho biết cạnh mỗi ô vuông bằng 1 cm. Tính độ dài các đoạn PQ, PR, RQ, AB, BC, CA trong Hình 11.

Lời giải:

Ta có:  $AB=\sqrt{2^2+4^2}=2\sqrt{5}$;

           $AC=\sqrt{2^2+4^2}=2\sqrt{5}$ ;

           $\mathrm{BC}=\sqrt{2^2+6^2}=2\sqrt{10}$.

Xét tam giác ABC có:

P là trung điểm của BC

Q lần lượt là trung điểm của AC

Do đó PQ là đường trung bình tam giác ABC.

Khi đó $\mathrm{PQ}=\frac{1}{2}AB=\frac{1}{2}.2\sqrt{5}=\sqrt{5}$

Tương tự:  $\mathrm{PR}=\frac{1}{2}AC=\frac{1}{2}.2\sqrt{5}=\sqrt{5}$;

                   $\mathrm{RQ}=\frac{1}{2}BC=\frac{1}{2}.2\sqrt{10}=\sqrt{10}$

Vậy $\mathrm{PQ}=\sqrt{5}$, $PR=\sqrt{5}$, $\mathrm{RQ}=\sqrt{10}$, $AB=2\sqrt{5}$, $AC=2\sqrt{5}$, $\mathrm{BC}=2\sqrt{10}$.

Bài 4 trang 54 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm hai cạnh bên AD và BC. Gọi K là giao điểm của AF và DC (Hình 12).

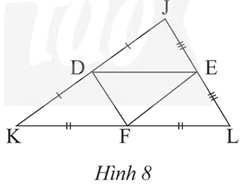
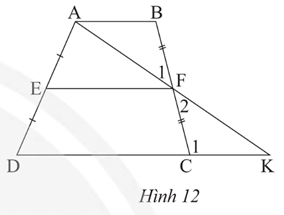
a) Tam giác FBA và tam giác FCK có bằng nhau không? Vì sao?

b) Chứng minh EF // CD // AB.

c) Chứng minh $\mathrm{EF}=\frac{AB+CD}{2}$

Lời giải:

a) Xét tam giác FBA và FCK ta có:

$\widehat{F_1}=\widehat{F_2}$ (hai góc đối đỉnh)

FB = FC (giả thiết)

$\widehat{FBA}=\widehat{FCK}$ (AB // CD, hai góc so le trong)

Do đó ΔFBA = ΔFCK (g.c.g)

b) ΔFBA = ΔFCK suy ra FA = FK

Xét tam giác ADK có:

EA = ED

FA = FK

Do đó, EF là đường trng bình tam giác ABC.

Suy ra EF // DK

Mà AB // CD nên EF // CD // AB.

c) EF là đường trung bình tam giác ADK.

Suy ra $EF=\frac{1}{2}DK=\frac{1}{2}(CD+CK)$

Mà CK = BA (do ΔFBA = ΔFCK)

Do đó $\mathrm{EF}=\frac{AB+CD}{2}$

Bài 5 trang 54 Toán 8 Tập 2: Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.

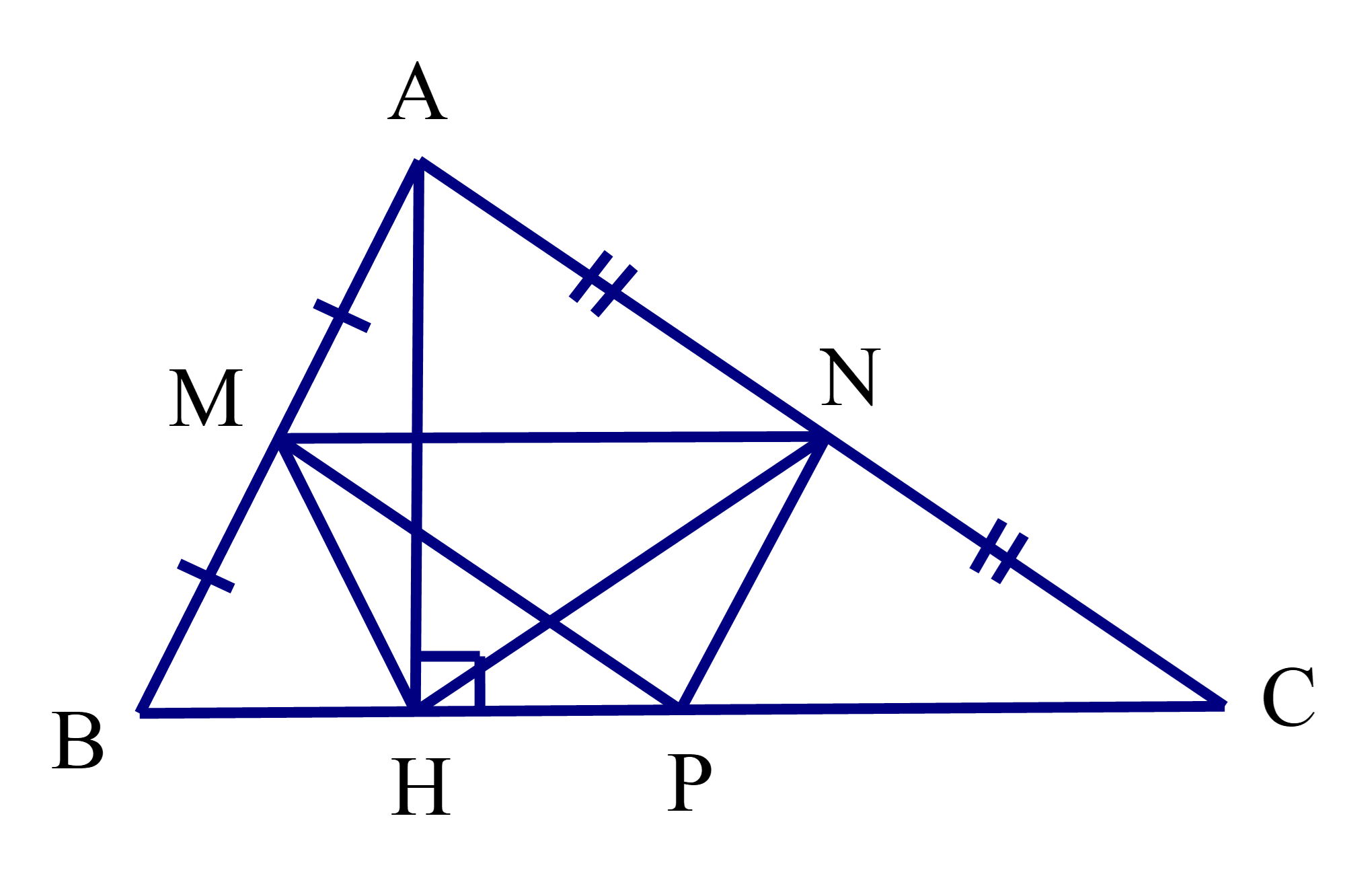
Lời giải:

Xét tam giác ABC ta có:

M là trung điểm của AB (gt);

N là trung điểm của AC (gt);

Do đó MN là đường trung bình của tam giác ABC nên MN // BC.

Suy ra tứ giác MNPH là hình thang.

Xét tam giác ABC ta có:

M là trung điểm của AB (gt);

P là trung điểm của BC;

Do đó MP là đường trung bình của tam giác ABC nên MN=$\frac{1}{2}AC$

Vì ΔACH vuông tại H có HN là trung tuyến (N là trung điểm của AC) nên NH=$\frac{1}{2}AC$

Mà MP=$\frac{1}{2}AC$ (cmt) nên NH = MP.

Hình thang MNPH (MN // PH) có MP = NH nên là hình thang cân.

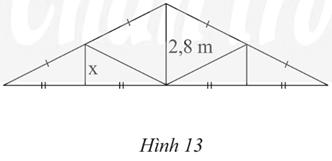
Bài 6 trang 54 Toán 8 Tập 2: Một mái nhà được vẽ lại như Hình 13. Tính độ dài x trong hình mái nhà.

Lời giải:

Xét tam giác ABH có:

AD = BD

BE = EH

Do đó DE là đường trung bình tam giác ABH nên $\mathrm{DE}=\frac{1}{2}AH$

Khi đó $x=\frac{1}{2}.2,8=1,4\left(m\right)$

Bài 7 trang 54 Toán 8 Tập 2: Ảnh chụp từ Google Maps của một trường học được cho trong Hình 14. Hãy tính chiều dài cạnh DE, cho biết BC = 232 m và B, C lần lượt là trung điểm AD và AE.

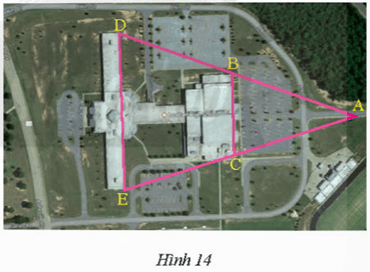
Lời giải:

Xét tam giác ADE có:

B là trung điểm AD

C là trung điểm AE

Do đó BC là đường trung bình của tam giác ADE.

Khi đó DE = 2BC = 2.232 = 464 (m).