Công thức về tính chất hai đường thẳng song song

 1. Công thức

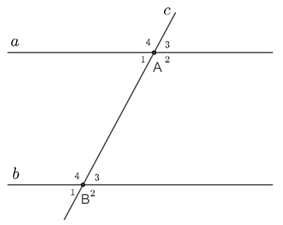
- Cho ba đường thẳng a, b, c phân biệt tạo thành các góc như hình vẽ.

+) Nếu a // b thì A1^=B1^, A2^=B2^, A3^=B3^, A4^=B4^(các cặp góc đồng vị bằng nhau)

Ngược lại, nếu A1^=B1^(hoặc A2^=B2^, hoặc A3^=B3^, hoặc A4^=B4^) (hai góc đồng vị bằng nhau) thì a // b.

+) Nếu a // b thì A1^=B3^, A2^=B4^(các cặp góc so le trong bằng nhau)

Ngược lại, nếu A1^=B3^(hoặc A2^=B4^) (hai góc so le trong bằng nhau) thì a // b.

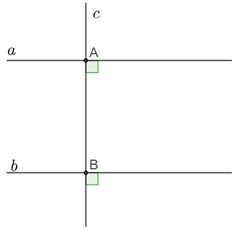
c⊥a;c⊥b suy ra a // b.

2. Ví dụ minh hoạ

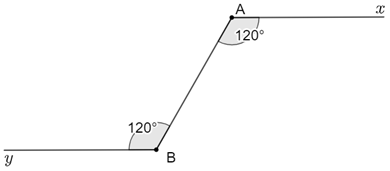
Ví dụ 1. Vẽ cặp góc so le trong xAB^, yBA^đều bằng 120°. Hỏi hai đường thẳng Ax và By có song song với nhau không? Vì sao?

Hướng dẫn giải:

Ta có: xAB^ = yBA^=120°

Mà hai góc xAB^, yBA^ở vị trí so le trong

Do đó Ax // By (dấu hiệu nhận biết hai đường thẳng song song).

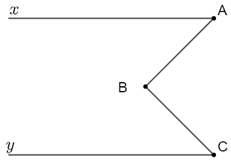
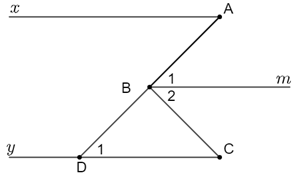
Ví dụ 2. Cho hình vẽ, biết ABC^=xAB^+BCy^. Chứng minh Ax // Cy.

Hướng dẫn giải:

Kẻ Bm nằm giữa BA và BC sao cho Bm // Ax.

Khi đó A^=B1^(hai góc so le trong) (1)

Theo giả thiết có ABC^=A^+C^nên ABC^=B1^+C^

Mà ABC^=B1^+B2^nên B2^=C^

Mà hai góc ở vị trí so le trong nên Cy // Bm.

Kéo dài tia AB cắt Cy tại D.

Vì Cy // Bm nên B1^=D1^(hai góc đồng vị)(2)

Từ (1) và (2) suy ra A^=D1^

Mà A^và D1^là hai góc so le trong

Nên Ax // Cy (dấu hiệu nhận biết)

Vậy Ax // Cy.

3. Bài tập tự luyện

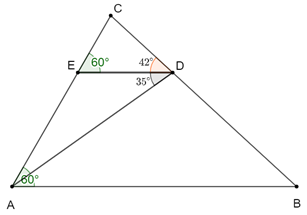
Bài 1. Cho hình vẽ. Tính ABC^; DAB^; CAD^; AED^.

Bài 2. Cho đường thẳng c cắt hai đường thẳng a, b tại A và B tạo thành cặp góc trong cùng phía bù nhau.

a) Vì sao hai góc so le trong trong mỗi cặp bằng nhau?

b) Vì sao hai góc đồng vị trong mỗi cặp bằng nhau?

Bài 3. Hãy chứng minh trên hình vẽ dưới đây ta có AB // CD.

Bài 4. Cho góc vuông xOy^, điểm A thuộc tia Ox. Kẻ tia Az vuông góc với Ox (tia Az nằm trong góc xOy^). Gọi Om là tia phân giác của góc xOy^, An là tia phân giác của góc xAz^. Chứng minh Om // An.

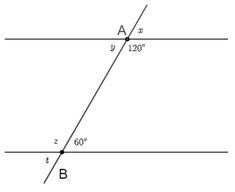
Bài 5. Tính các giá trị x, y, z, t trên hình.