Chương 1 Đại số
I. Căn bậc hai
1. Một số công thức cần nhớ
2. Điều kiện để căn thức có nghĩa
3. Điều kiện có nghĩa của một số biểu thức
4. Tính chất của căn bậc hai
Với hai số a và b không âm, ta có:
5. Các công thức biến đổi căn thức
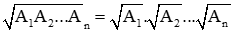
+) Đưa thừa số A2 ra ngoài dấu căn bậc hai ta được |A|.
+) Đưa thừa số vào trong dấu căn bậc hai:
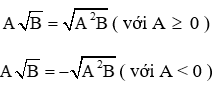
+) Khử mẫu của biểu thức dưới dấu căn bậc hai:
Ta nhân mẫu số với thừa số phụ thích hợp để mẫu số là một bình phương
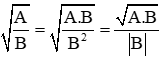
+) Trục căn thức ở mẫu số:
Dạng 1: Mẫu là biểu thức dạng tích các căn thức và các số, ta nhân tử và mẫu với căn thức.
Dạng 2: Mẫu là biểu thức dạng tổng có căn thức, ta nhân tử và mẫu với biểu thức liên hợp của mẫu.
6. Phương trình chứa căn thức bậc hai
II. Căn bậc ba
Chương 2
1. Hàm số bậc nhất
a. Khái niệm hàm số bậc nhất
- Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b. Trong đó a, b là các số cho trước và a ≠ 0
b. Tính chất: Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có tính chất sau:
- Đồng biến trên R khi a > 0
- Nghịch biến trên R khi a < 0
c. Đồ thị của hàm số y = ax + b (a ≠ 0)
Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng
- Cắt trục tung tại điểm có tung độ bằng b
- Song song với đường thẳng y = ax, nếu b ≠ 0, trùng với đường thẳng y = ax, nếu b = 0
* Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0)
Bước 1. Cho x = 0 thì y = b ta được điểm P(0; b) thuộc trục tung Oy.
Cho y = 0 thì x = 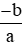
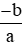
Bước 2. Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b
d. Vị trí tương đối của hai đường thẳng
Cho hai đường thẳng (d): y = ax + b (a ≠ 0) và (d’): y = a’x + b’ (a’ ≠ 0). Khi đó:
e. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)
* Góc tạo bởi đường thẳng y = ax + b và trục Ox.
- Góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tạo bởi tia Ax và tia AT, trong đó A là giao điểm của đường thẳng y = ax + b với trục Ox, T là điểm thuộc đường thẳng y = ax + b và có tung độ dương
* Hệ số góc của đường thẳng y = ax + b
- Hệ số a trong phương trình y = ax + b được gọi là hệ số góc của đường thẳng: y = ax + b
f. Một số phương trình đường thẳng
- Đường thẳng đi qua điểm M0(x0; y0) có hệ số góc k: y = k(x – x0) + y0
- Đường thẳng đi qua điểm A(x0, 0) và B(0; y0) với x0.y0 ≠ 0 là
2. Công thức tính toạ độ trung điểm của đoạn thẳng và độ dài đoạn thẳng
Cho hai điểm phân biệt A với B với A(xA, yB) và B(xA, yB). Khi đó
- Độ dài đoạn thẳng AB được tính bởi công thức
- Tọa độ trung điểm M của AB được tính bởi công thức
Chương 3
I. CÁC KHÁI NIỆM:
Phương trình bậc nhất hai ẩn:
+ Dạng: ax + by = c trong đó a; b; c là các hệ số đã biết (a ≠ 0 hoặc b ≠ 0)
+ Một nghiệm của phương trình là cặp số x0; y0 thỏa mãn: ax0 + by0 = c
+ Phương trình bậc nhất hai ẩn ax + by = c luôn luôn có vô số nghiệm.
+ Tập nghiệm được biểu diễn bởi đường thẳng (d): ax + by = c. Nếu a ≠ 0; b ≠ 0 thì đường thẳng (d) là đồ thị của hàm số bậc nhất:
Hệ hai phương trình bậc nhất hai ẩn:
+ Dạng: 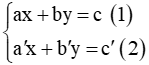
+ Nghiệm của hệ là nghiệm chung của hai phương trình
+ Nếu hai phương trình ấy không có nghiệm chung thì ta nói hệ vô nghiệm
+ Quan hệ giữa số nghiệm của hệ và đường thẳng biểu diễn tập nghiệm:
- Phương trình (1) được biểu diễn bởi đường thẳng (d)
- Phương trình (2) được biểu diễn bởi đường thẳng (d')
* Nếu (d) cắt (d') hệ có nghiệm duy nhất
* Nếu (d) song song với (d') thì hệ vô nghiệm
* Nếu (d) trùng (d') thì hệ vô số nghiệm.
Hệ phương trình tương đương:
Hai hệ phương trình được gọi là tương đương với nhau nếu chúng có cùng tập nghiệm
II. PHƯƠNG PHÁP GIẢI HỆ PHƯƠNG TRÌNH:
1. Giải hệ phương trình bằng phương pháp thế:
+ Bước 1: Từ một phương trình của hệ đã cho, ta biểu diễn một ẩn theo ẩn kia, rồi thay vào phương trình thứ hai để được một phương trình mới (chỉ còn 1 ẩn).
+ Bước 2: Dùng phương trình mới này để thay thế cho phương trình thứ hai trong hệ (phương trình thứ nhất cũng thường được thay thế bởi hệ thức biểu diễn một ẩn theo ẩn kia có được ở bước 1).
2. Giải hệ phương trình bằng phương pháp cộng đại số:
+ Bước 1: Cộng hay trừ từng vế hai phương trình của hệ của hệ phương trình đã cho để được một phương trình mới.
+ Bước 2: Dùng phương trình mới ấy thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia)
Lưu ý: Khi các hệ số của cùng một ẩn đối nhau thì ta cộng vế theo vế của hệ.
Khi các hệ số của cùng một ẩn bằng nhau thì ta trừ vế theo vế của hệ.
Khi hệ số của cùng một ẩn không bằng nhau cũng không đối nhau thì ta chọn nhân với số thích hợp để đưa về hệ số của cùng một ẩn đối nhau (hoặc bằng nhau).
(tạm gọi là quy đồng hệ số)
Chương 4
I. HÀM SỐ y = ax2 (a ≠ 0). ĐỒ THỊ HÀM SỐ y = ax2 (a ≠ 0)
1. Tính chất hàm số y = ax2 (a ≠ 0)
a) Tính chất:
Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
Nếu a < 0 thì hàm số nghịch biến khi x > 0 và đồng biến khi x < 0
b) Nhận xét:
Nếu a > 0 thì y > 0 với mọi x khác 0; y = 0 khi x = 0. Giá trị nhỏ nhất của hàm số là y = 0.
Nếu a < 0 thì y < 0 với mọi x khác 0; y = 0 khi x = 0. Giá trị lớn nhất của hàm số là y = 0.
2. Tính chất của đồ thị hàm số
● Đồ thị hàm số y = ax2 (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục Oy là trục đối xứng. Đường cong đó được gọi là một Parabol với đỉnh O.
● Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O(0;0) là điểm thấp nhất của đồ thị.
● Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O(0;0) là điểm cao nhất của đồ thị.
II. PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
1. Định nghĩa: Pt bậc hai một ẩn là pt có dạng: ax2 + bx + c = 0 (a ≠ 0) (1), trong đó x là ẩn; a, b, c là các số cho trước.
2. Cách giải
a) Khuyết c (c = 0): pt (1) trở thành:
b) Khuyết b (b = 0): pt (1) trở thành:
- Nếu 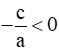
- Nếu
c) Đầy đủ: ax2 + bx + c = 0 (a ≠ 0)
Công thức nghiệm | Công thức nghiệm thu gọn |
|---|---|
Δ = b2 - 4ac + Nếu Δ > 0 thì pt có 2 nghiệm phân biệt: + Nếu Δ = 0 thì pt có nghiệm kép: + Nếu Δ < 0 thì pt vô nghiệm | Δ' = b'2 - ac + Nếu Δ' > 0 thì pt có 2 nghiệm phân biệt: + Nếu Δ' = 0 thì pt có nghiệm kép: + Nếu Δ' < 0 thì pt vô nghiệm |
d) Cho pt: ax2 + bx + c = 0 (a ≠ 0). Điều kiện để phương trình:
- Vô nghiệm: Δ < 0 (Δ' < 0)
- Nghiệm kép: Δ = 0 (Δ' = 0)
- Có 2 nghiệm phân biệt: Δ > 0 (Δ' > 0) hoặc a.c < 0
III. HỆ THỨC VI-ÉT VÀ ỨNG DỤNG
- Định lý: Nếu x1; x2 là 2 nghiệm của pt ax2 + bx + c = 0 (a ≠ 0) thì:
- Ứng dụng nhẩm nghiệm của hệ thức Vi-ét:
+ Nếu pt ax2 + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì pt có 2 nghiệm là:
+ Nếu pt ax2 + bx + c = 0 (a ≠ 0) có a - b + c = 0 thì pt có 2 nghiệm là:
+ Nếu 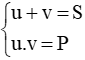
IV. PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI
1. Phương trình trùng phương.
- Dạng tổng quát: ax4 + bx2 + c = 0 (a ≠ 0)
- Cách giải: dùng phương pháp đặt ẩn phụ, đặt x2 = t (t ≥ 0). Khi đó ta có pt: at2 + bt + c = 0 (đây là pt bậc hai một ẩn)
2. Phương trình chứa ẩn ở mẫu: Các bước giải
- Tìm ĐKXĐ của pt
- Quy đồng mẫu thức cả 2 vế của pt, rồi khử mẫu
- Giải pt vừa nhận được
- Kết luận: so sánh nghiệm tìm được với ĐKXĐ của pt
3. Phương trình tích.
Công thức Hình học lớp 9
Chương 1
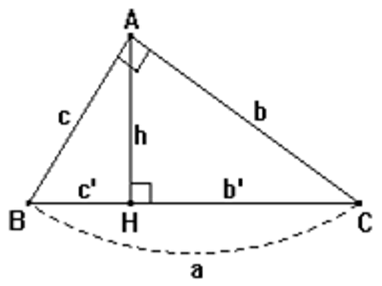
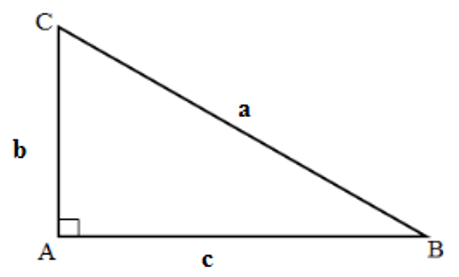
1. Hệ thức lượng trong tam giác vuông.
Cho tam giác ABC có đường cao AH
Đặt BC = a; AC = b; AB = c; AH = h; CH = b'; BH = c'
BH, CH lần lượt là hình chiếu của AB và AC lên BC.
Ta có các hệ thức sau:
+) b2 = ab' ; c2 = ac'
+) h2 = b'c'
+) ah = bc
+) a2 = b2 + c2 (Định lý Py-ta-go)
+)
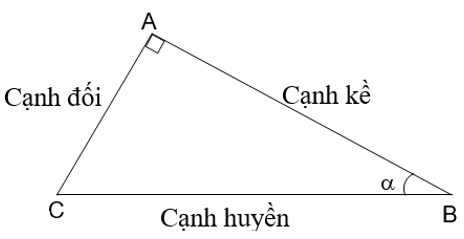
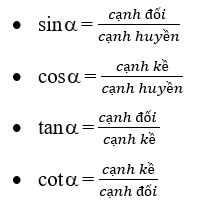
2. Tỉ số lượng giác của góc nhọn
a) Định nghĩa
b) Tính chất
+) Cho hai góc α và β phụ nhau. Khi đó
● sin = cos; ● tan = cot;
● cos = sin ; ● cot = tan.
+) Cho góc nhọn α. Ta có
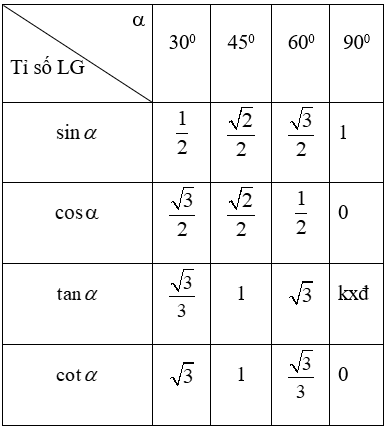
d) Tỉ số lượng giác của các góc đặc biệt
3. Hệ thức về cạnh và góc trong tam giác vuông
● b = asinB = acosC
● b = ctanB = ccotC
● c = asinC = acosB
● c = btanC = bcot B
Chương 2
1. Sự xác định đường tròn.
- Một đường tròn được xác định khi biết tâm O và bán kính R của đường tròn đó (kí hiệu (O;R)), hoặc khi biết một đoạn thẳng là đường kính của đường tròn đó
- Có vô số đường tròn đi qua hai điểm. Tâm của chúng nằm trên đường trung trực của đoạn thẳng nối hai điểm đó.
- Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
Chú ý: Không vẽ được đường tròn nào đi qua ba điểm thẳng hàng.
- Đường tròn đi qua ba đỉnh của tam giác gọi là đường tròn ngoại tiếp tam giác, tam giác gọi là tam giác nội tiếp đường tròn.
2. Tính chất đối xứng của đường tròn.
+) Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
- Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
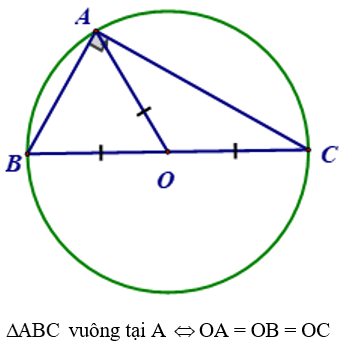
+) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền
- Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
3. Quan hệ giữa đường kính và dây của đường tròn
- Trong các dây của một đường tròn, dây lớn nhất là đường kính.
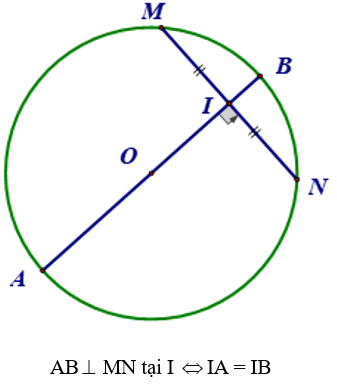
- Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
- Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy
4. Liên hệ giữa dây và khoảng cách từ tâm đến dây
Định lí 1: Trong một đường tròn:
- Hai dây bằng nhau thì cách đều tâm
- Hai dây cách đều tâm thì bằng nhau
AB = CD ⇔ OH = OK
Định lí 2: Trong hai dây của một đường tròn
- Dây nào lớn hơn thì dây đó gần tâm hơn
- Dây nào gần tâm hơn thì dây đó lớn hơn
MN > CD ⇔ OI < OK
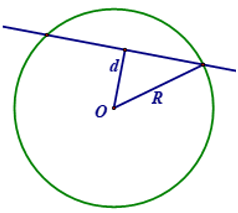
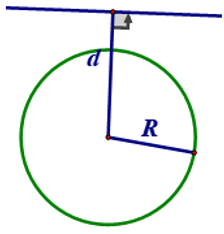
5. Vị trí tương đối của đường thẳng và đường tròn: d là khoảng cách từ tâmcủa đường tròn đến đường thẳng, R là bán kính
Vị trí tương đối của đường thẳng và đường tròn | Số điểm chung | Hệ thức giữa d và R |
|---|---|---|
Đường thẳng và đường tròn cắt nhau | 2 | d < R |
Đường thẳng và đường tròn tiếp xúc nhau | 1 | d = R |
Đường thẳng và đường tròn không giao nhau | 0 | d > R |
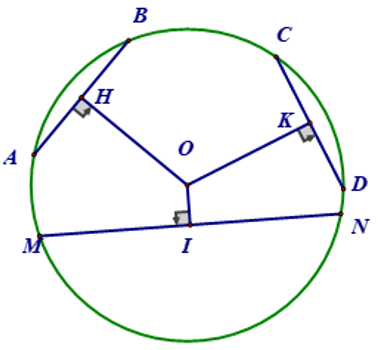
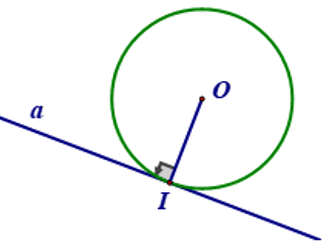
☞ Định lí: Nếu một đường thẳng alà tiếp tuyến của một đường tròn (O) thì nó vuông góc với bán kính đi qua tiếp điểm.
Đường thẳng a là tiếp tuyến của (O) ⇔ a ⊥OI
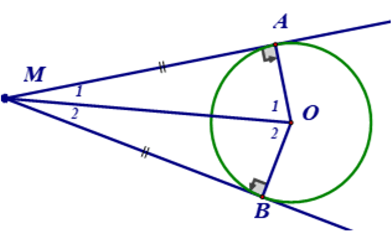
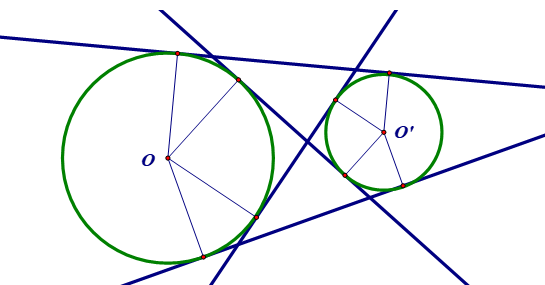
6. Tính chất của hai tiếp tuyến cắt nhau
Định lí: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
- Điểm đó cách đều hai tiếp điểm
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
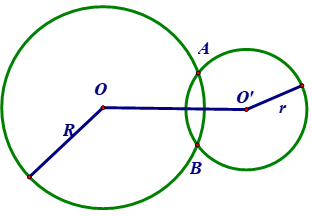
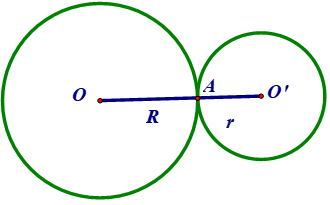
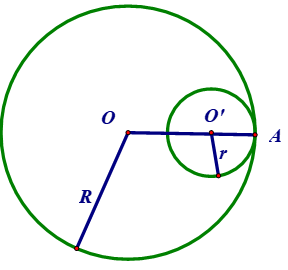
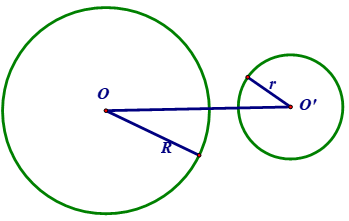
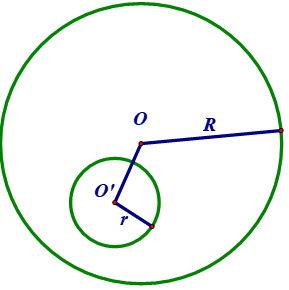
7. Vị trí tương đối của hai đường tròn
Cho (O ; R) và (O’; r) với R >r
VỊ TRÍ | HÌNH | SỐ ĐIỂM CHUNG | HỆ THỨC |
|---|---|---|---|
Cắt nhau | 2 A, B được gọi là 2 giao điểm | R – r < OO’ < R + r | |
Tiếp xúc ngoài | 1 A gọi là tiếp điểm | OO’ = R + r | |
Tiếp xúc trong | 1 A gọi là tiếp điểm | OO’ = R – r > 0 | |
Không giao nhau ((O) và (O’) ở ngoài nhau) | 0 | OO’ > R + r | |
Không giao nhau ((O) đựng (O’) ) | 0 | OO’ < R – r |
Định lí: Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung.
{A;B} = (O) ∩ (O') ⇔ OO' là trung trực của AB
+) Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
(O) tiếp xúc (O') tại A ⇔ A ∈ OO'
- Tiếp tuyến chung của hai đường tròn: Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó.
Chương 3
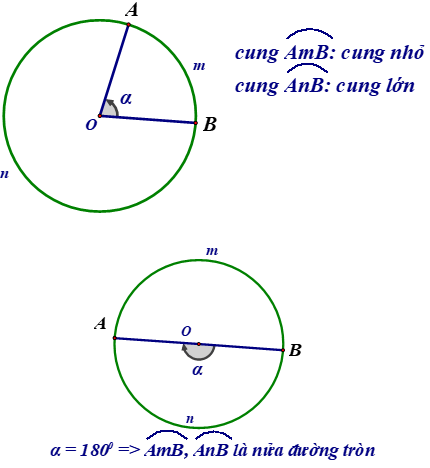
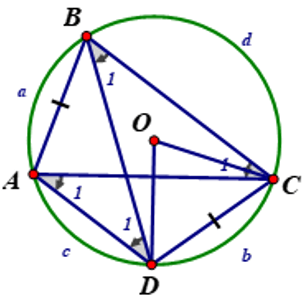
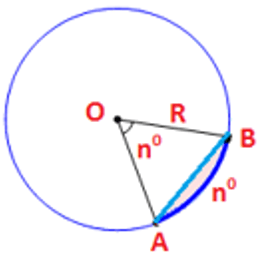
1. Góc ở tâm. Số đo cung
Định lí: Nếu C là một điểm nằm trên cung AB thì:
2. Liên hệ giữa cung và dây
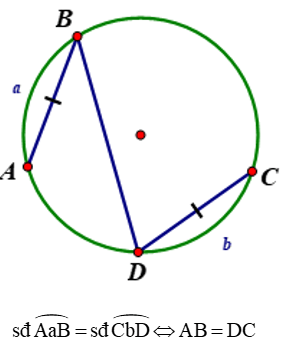
Định lí 1: Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
- Hai cung bằng nhau căng hai dây bằng nhau
- Hai dây bằng nhau căng hai cung bằng nhau
Định lí 2: Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
- Cung lớn hơn căng dây lớn hơn
- Dây lớn hơn căng cung lớn hơn
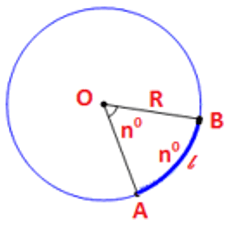
3. Góc nội tiếp
- Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn:
Hệ quả: Trong một đường tròn:
- Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
- Góc nội tiếp (nhỏ hơn hoặc bằng 900) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
- Góc nội tiếp chắn nửa đường tròn là góc vuông.
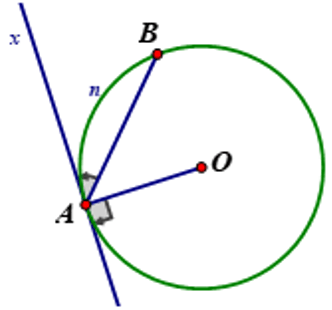
4. Góc tạo bởi tia tiếp tuyến và dây cung
Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
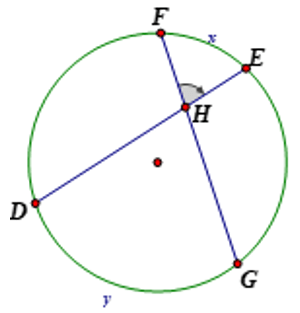
5. Góc có đỉnh ở bên trong đường tròn là góc có đỉnh nằm bên trong đường tròn.
Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
6. Góc có đỉnh ở bên ngoài đường tròn:
Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
7. Tứ giác nội tiếp
- Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 1800.
+) Dấu hiệu nhận biết tứ giác nội tiếp:
- Tứ giác có tổng hai góc đối diện bằng 1800.
- Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện
- Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác
- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc bằng nhau.
8. Các công thức
- Công thức tính độ dài đường tròn: C = 2πR = πd
- Công thức tính độ dài cung tròn:
Trong đó: R là bán kính, l là độ dài của một cung n0
Chương 4
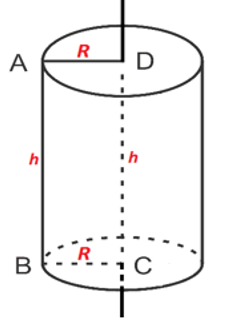
1. Hình trụ: Khi quay hình chữ nhật một vòng quanh một cạnh cố định, ta được một hình trụ
- Diện tích xung quanh: Sxq = 2πRh
- Diện tích toàn phần: Stp = Sxq + 2.Sđáy
- Thể tích: V = S.h = πR2h
Trong đó: S là diện tích đáy, h là chiều cao, R là bán kính đáy
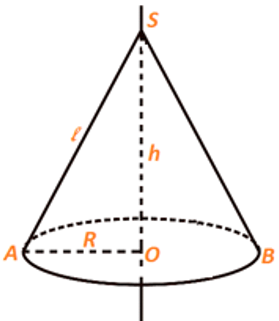
2. Hình nón: Khi quay tam giác vuông một vòng quanh một cạnh góc vuông cố định thì được một hình nón
- Diện tích xung quanh: Sxq = πR.l
- Diện tích toàn phần: Stp = Sxq + Sđáy
Stp = πRl + πR2
Trong đó: h là chiều cao, R là bán kính đáy, l là đường sinh
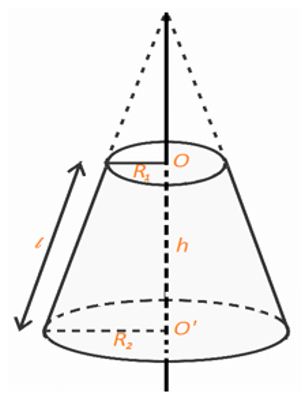
3. Hình nón cụt: Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần mặt phẳng nằm trong hình nón là một hình tròn. Phần hình nón nằm giữa mặt phẳng nói trên và mặt đáy được gọi là một hình nón cụt.
Trong đó: h là chiều cao, R1, R2 là hai bán kính đáy, l là đường sinh
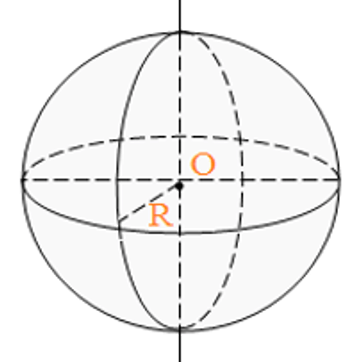
4. Hình cầu: Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu. Nửa đường tròn trong phép quay nói trên tạo nên mặt cầu.
Trong đó: R là bán kính của mặt cầu, d là đường kính mặt cầu


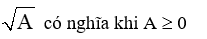
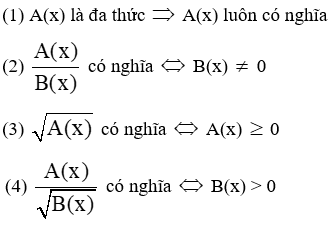
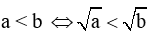
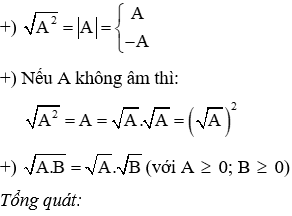
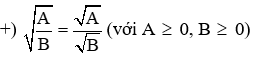
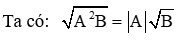
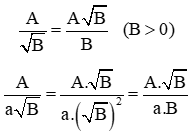
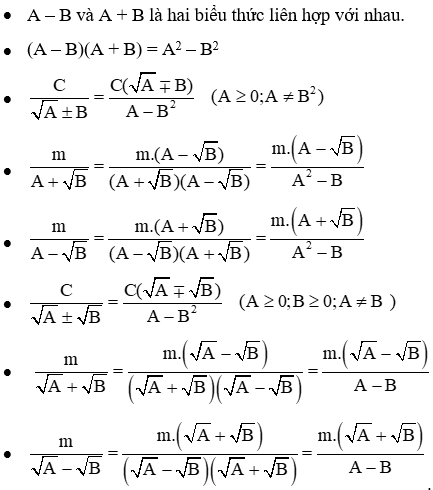
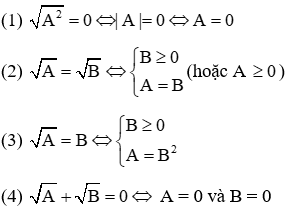
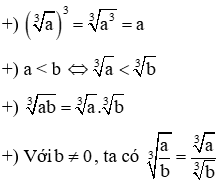
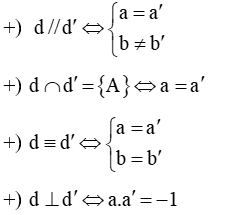
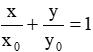
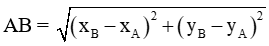
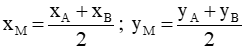
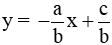

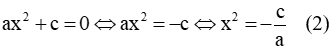
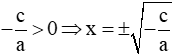
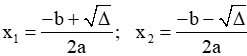
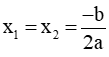
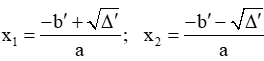
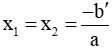

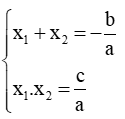
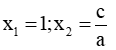
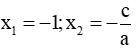
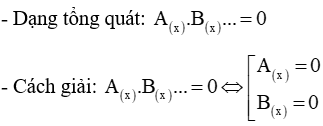
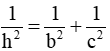
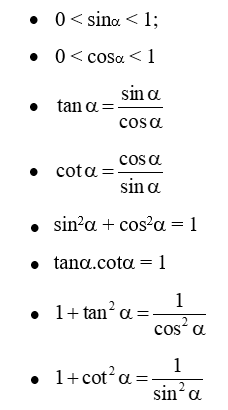

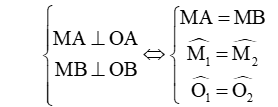
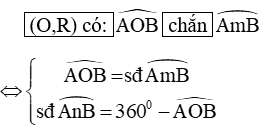
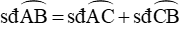
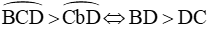
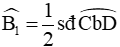
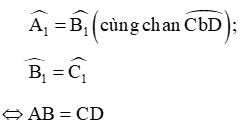
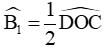
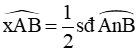
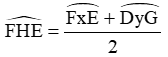
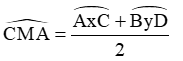

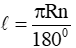
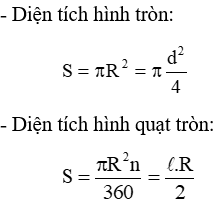
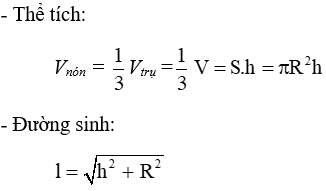
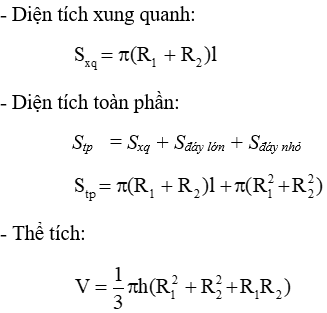
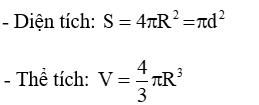
0 Comments:
Đăng nhận xét