Câu 1: Cho tam giác ABC có các tia phân giác cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB lại E, cắt AC tại F. Biết BE = 1 cm, CF = 2 cm. Độ dài đoạn EF là:
Câu 2: Cho tam giác MNP có trung tuyến MA, NC cắt nhau tại O. Biết MO = 2,5 cm, OC = 1 cm. Độ dài các đường trung tuyến MA, NC lần lượt là:
- 3 cm và 3,75 cm;
- 3,75 cm và 3 cm;
- 2,5 cm và 1 cm;
- 1 cm và 2,5 cm.
Câu 3: Cho tam giác ABC vuông cân tại A. Trên cạnh AC lấy điểm E sao cho góc ABE bằng 30°. Trên tia đối của tia AB lấy F sao cho AF = AE. Vẽ điểm I sao cho FC là trung trực của EI. Số đo góc BFI là:
Câu 4: Cho tam giác ABC có trung tuyến AM và BN là hai đường trung tuyến, AM = BN. Tam giác ABC là tam giác gì?
- Tam giác ABC vuông tại A;
- Tam giác ABC cân tại C;
- Tam giác ABC cân tại B;
- Tam giác ABC cân tại A.
Câu 5: Cho tam giác ABC vuông tại A, trên tia BA lấy M sao cho BM = BC. Tia phân giác góc B cắt AC tại H. Khẳng định nào sau đây là sai?
- MH ⊥ BC;
- H là trực tâm tam giác MBC;
- MH = HC;
- Cả A, B, C đều đúng.
Câu 6: Cho tam giác MNP cân tại M. Hai đường trung tuyến NE, PF cắt nhau tại I. Kéo dài MI cắt NP tại H. Chọn phát biểu sai trong các phát biểu sau:
- H là trung điểm của NP;
- I là trọng tâm tam giác MNP;
- IE là trung trực của MP;
- MH là trung trực của NP.
Câu 7: Cho tam giác MNP có chu vi bằng 70 cm, biết MN : NP = 2 : 3 và NP : MP = 4 : 5. Trong ba góc của tam giác MNP, góc nào nhỏ nhất?
- Góc M;
- Góc N;
- Góc P;
- Ba góc bằng nhau.
Câu 8: Cho hình vẽ, biết rằng BC = 10 cm; AD = 16 cm và chu vi ∆ABC bằng 24 cm.
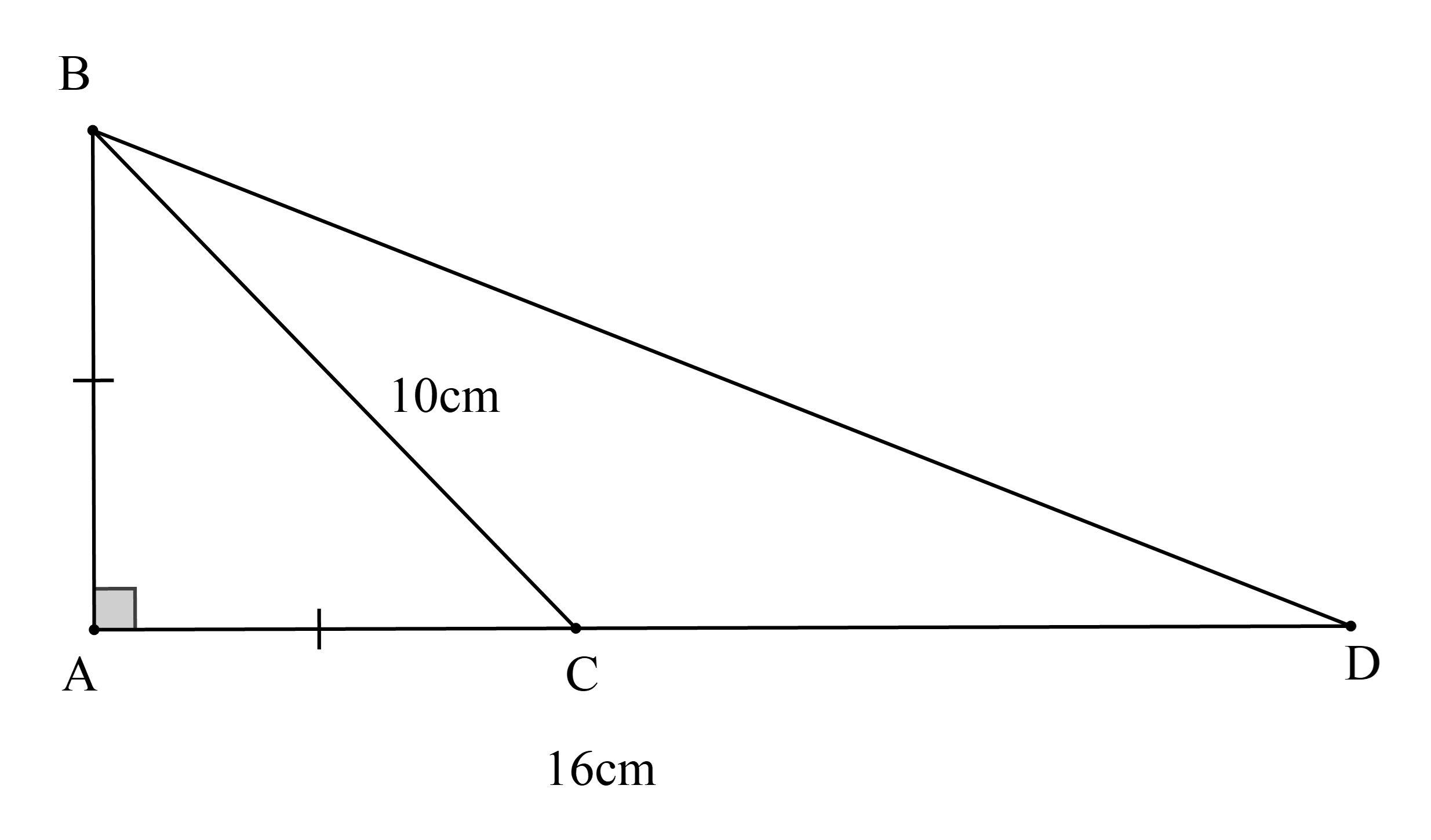
Diện tích ∆BCD là
- 24,5 cm$^{2}$
- 31,5 cm$^{2}$
- 56 cm$^{2}$
- 65 cm$^{2}$
Câu 9: Cho hình thang cân ABCD và ABKH là hình chữ nhật như hình vẽ.
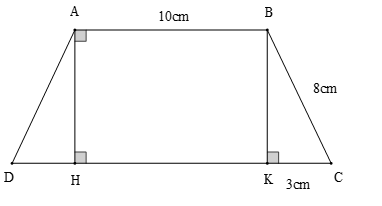
Chu vi tứ giác ABCD là
- 42 cm;
- 46 cm;
- 50 cm;
- 54 cm.
Câu 10: Cho ∆ABC có AB = 10 cm; BC = 6 cm. Qua trung điểm M của AC, kẻ đường vuông góc với AC cắt AB tại K. Chu vi ∆KBC là
- 14 cm;
- 28 cm;
- 16 cm;
- 30 cm.
Câu 11: Cho tam giác ABC vuông tại C có CH là đường cao. Trên cạnh AB lấy điểm M sao cho BM = BC. Kẻ MN vuông góc với AC tại N. Chọn khẳng định đúng:
- AC + BC > AB + CH;
- AC + BC ≥ AB + CH;
- AC + BC < AB + CH;
- AC + BC ≤ AB + CH.
Câu 12: Cho tam giác ABC nhọn có BM và CN là hai đường cao. Trên tia đối của BM lấy P sao cho BP = AC, trên tia đối của CN lấy Q sao cho CQ = AB. Chọn khẳng định đúng?
- AP = AQ;
- AP < AQ;
- AP > AQ;
- AP = 2AQ.
Câu 13: Cho ΔABC cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khẳng định nào đúng?
- I cách đều ba đỉnh của ΔABC;
- A, I, G thẳng hàng;
- G cách đều ba cạnh của ΔABC;
- Cả A, B, C đều đúng.
Câu 14: Cho đoạn thẳng AB = 5 cm. Vẽ đường tròn tâm A, bán kính 4 cm và đường tròn tâm B, bán kính 3 cm. Hai đường tròn này cắt nhau tại D và E. Khẳng định nào sau đây đúng nhất?
- A thuộc đường trung trực của đoạn thẳng DE;
- B thuộc đường trung trực của đoạn thẳng DE;
- AB là đường trung trực của đoạn thẳng DE;
- Cả A, B, C đều đúng.
Câu 15: Cho góc xOy có số đo là 50º, điểm A nằm trong góc xOy. Vẽ điểm M sao cho Ox là trung trực của AM, vẽ điểm N sao cho Oy là trung trực của AN. Số đo góc MON là:
Câu 16: Cho ∆ABC vuông tại A, M là trung điểm của AC. Kẻ AD và CE vuông góc với BM. Chọn khẳng định đúng:
- BD + BE > 2AB;
- BD + BE > 2BM;
- BD + BE < 2BM;
- BD + BE < 2AB.
Câu 17: Cho tam giác ABC có AB < AC. Trên AC lấy điểm D sao cho AB = CD. O là giao điểm của các đường trung trực của BD và AC. Phát biểu nào sau đây là đúng?
- ΔABO = ∆COD;
- ΔAOB = ∆COD;
- ΔABO = ∆CDO;
- ΔBOA = ∆COD.
Câu 18: Cho ∆ABC cân tại A có BC = 8 cm; chu vi của ∆ABC bằng 28 cm. Độ dài cạnh AC là
- 10 cm;
- 14 cm;
- 16 cm;
- 20 cm.
Câu 19: Cho hình vẽ, biết rằng BE, CF lần lượt là tia phân giác của $\widehat{ABC},\widehat{ACB}$ và $\widehat{ABE}=38°,\widehat{BCF}=25°$.
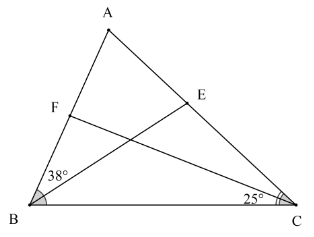
Số đo của $\widehat{A}$ là
Câu 20: Cho tam giác ABC có AB < AC. Trên AC lấy điểm D sao cho AB = CD. O là giao điểm của các đường trung trực của BD và AC. Phát biểu nào sau đây là đúng?
- AO là đường trung trực của tam giác ABC;
- AO là tia phân giác của góc BAC;
- AO ⊥ BC;
- Cả A, B, C đều sai.
Hãy trả lời các câu hỏi để biết kết quả của bạn




0 Comments:
Đăng nhận xét