C1 _ Bài 3. Lũy thừa của một số hữu tỉ trang 18

 

Lý thuyết

1. Lũy thừa với số mũ tự nhiên

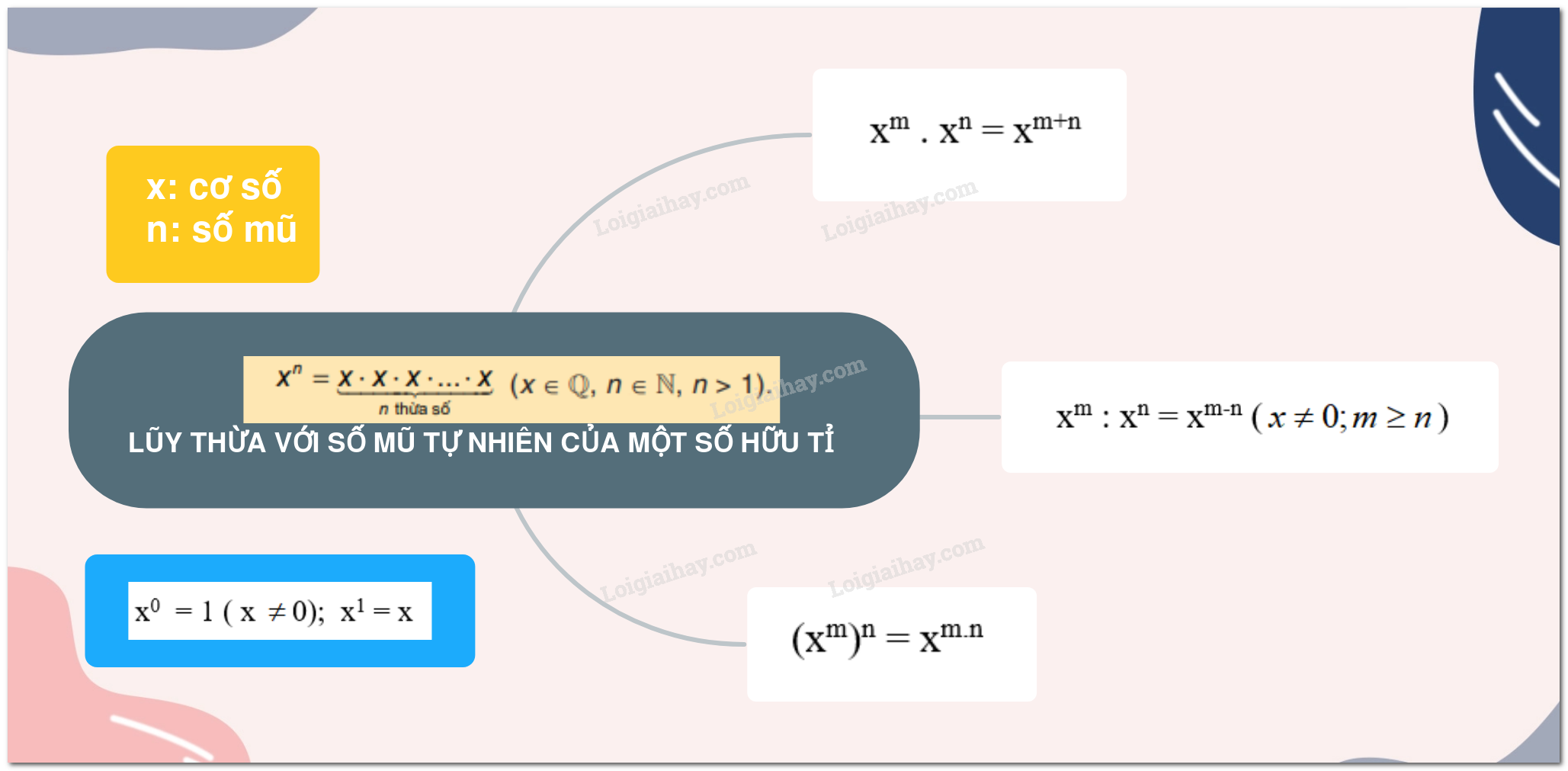
Lũy thừa bậc n của một số hữu tỉ x , kí hiệu xⁿ , là tích của n thừa số x ( n là số tự nhiên lớn hợn 1)

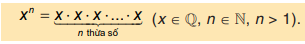
xⁿ đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x.
x: cơ số
n: số mũ
Quy ước: x⁰  = 1 ( x $\ne$$\ne$0);  x¹ = x

Chú ý:

$\begin{array}{c}(x.y{)}^n=x^n.y^n\\ (\frac{x}{y}{)}^n=\frac{x^n}{y^n}\end{array}$

+ Lũy thừa số mũ chẵn của 1 số hữu tỉ luôn dương
+ Lũy thừa số mũ lẻ của 1 số hữu tỉ âm luôn âm
+ Lũy thừa số mũ chẵn của 1 số hữu tỉ dương luôn dương
2. Tích và thương hai lũy thừa cùng cơ số
+ Khi nhân 2 lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng 2 số mũ

x^m . xⁿ = x^m+n

+ Khi chia 2 lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi lũy thừa của số chia

x^m : xⁿ = x^m-n ($x\ne 0;m\ge n$)

Ví dụ: 7⁴ . 7⁸ = 7⁴⁺⁸ = 7¹²

7⁵ : (-7)² = 7⁵ : 7² = 7^5-2 = 7³

3. Lũy thừa của lũy thừa

Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.

(x^m)ⁿ = x^m.n

Ví dụ: [(-3)³]⁴ = (-3)^3.4 = (-3)¹²

4. Mở rộng 

Lũy thừa với số mũ nguyên âm của một số hữu tỉ

$x^{-n}=\frac{1}{x^n}(x\ne 0)$

Ví dụ: $3^{-2}=\frac{1}{3^2}$