C1 _ Bài 1. Tập hợp các số hữu tỉ trang 6

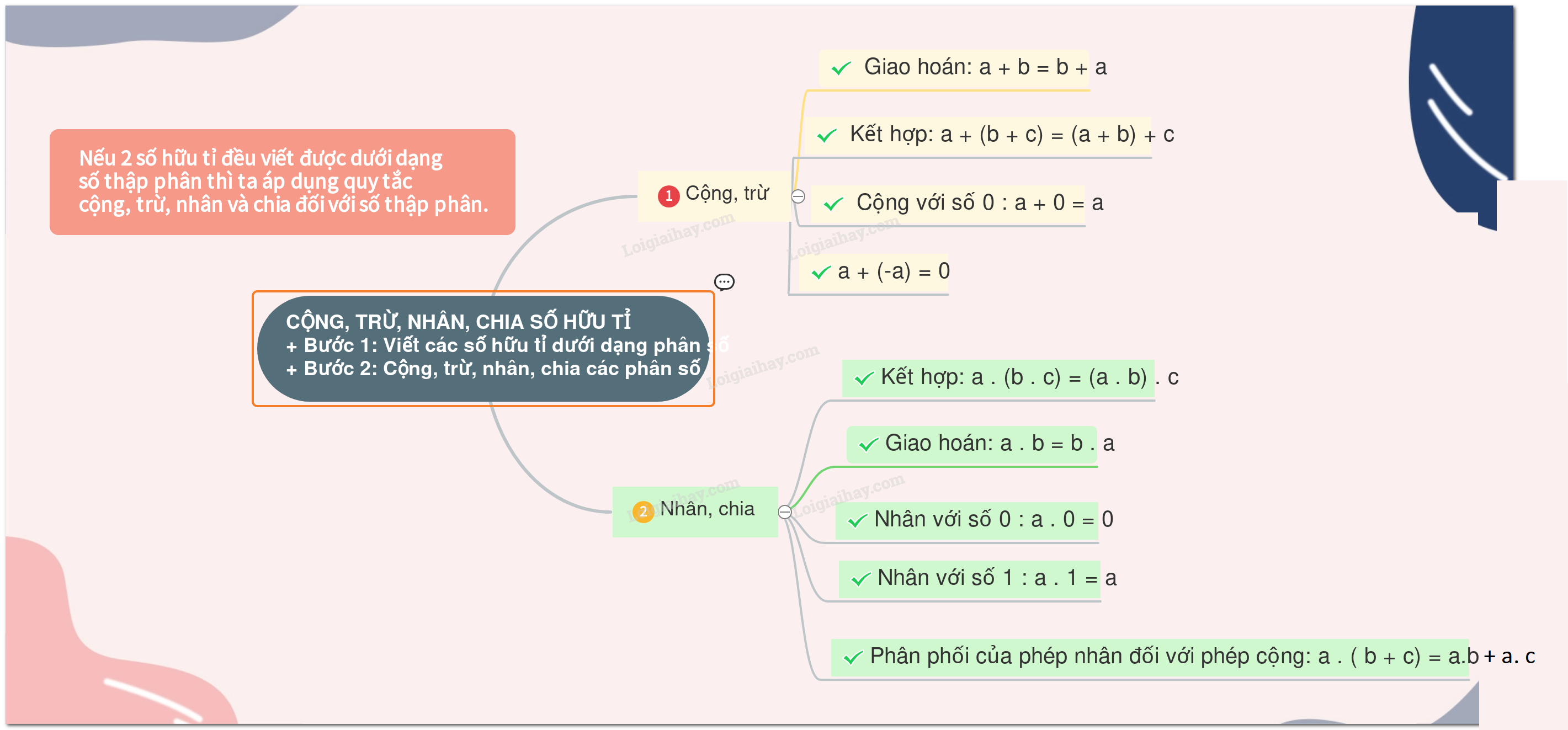
Lý thuyết 

1. Số hữu tỉ

Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}(a,b\in Z;b\ne 0)$

Tập hợp các số hữu tỉ được kí hiệu là Q

    Ví dụ: $-7,21;\frac{-7}{-9};\frac{0}{-2};2\frac{3}{8};...$ là các số hữu tỉ

Chú ý :

    + Các số thập phân đã biết đều là các số hữu tỉ. Các số nguyên, hỗn số cũng là các số hữu tỉ

    + Các phân số bằng nhau là các cách viết khác nhau của cùng một số hữu tỉ

     Ví dụ: - $\frac{9}{30}$= $\frac{-3}{10}$ nên 2 phân số - $\frac{9}{30}$ và $\frac{-3}{10}$ cùng biểu diễn 1 số hữu tỉ

2. So sánh hai số hữu tỉ

    + Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh 2 phân số đó.

    + Với 2 số hữu tỉ a và b bất kì, ta luôn có hoặc a = b, hoặc a < b, hoặc a > b

    + Cho 3 số hữu tỉ a, b, c. Nếu a < b; b < c thì a < c ( Tính chất bắc cầu)

    + Trên trục số, nếu a < b thì điểm a nằm trước điểm b

    + Các số hữu tỉ lớn hơn 0 gọi là các số hữu tỉ dương.

    + Các số hữu tỉ nhỏ hơn 0 gọi là các số hữu tỉ âm.

    + Số 0 không là số hữu tỉ âm, cũng không là số hữu tỉ dương.

Chú ý: Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm; các điểm nằm sau gốc O biểu diễn số hữu tỉ dương.

* Cách so sánh hai số hữu tỉ:

Ta viết chúng về cùng dạng phân số (hoặc dạng số thập phân) rồi so sánh chúng.

3. Biểu diễn số hữu tỉ trên trục số

    Ta có thể biểu diễn mọi số hữu tỉ trên trục số

    Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a.

    Ta chọn phân số tối giản để biểu diễn số hữu tỉ.

4. Số đối của một số hữu tỉ

    + Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ $\Large\frac{a}{b}$ $\frac{�}{�}$ là số hữu tỉ -$\Large\frac{a}{b}$$\frac{�}{�}$

Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a.

Trên trục số, 2 điểm biểu diễn 2 số hữu tỉ đối nhau a và –a nằm về 2 phía khác nhau so với điểm O và có cùng khoảng cách đến O.

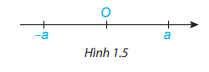
Ví dụ: -5 là số đối của 5

Giải mục 1 trang 6

Video hướng dẫn giải

HĐ 1

Cho các số $-7;0,5;0;1\frac{2}{3}$. Với mỗi số, hãy viết một phân số bằng số đã cho.

Phương pháp giải:

-          Đối với số nguyên: $a=\frac{a}{1}$

-          Đối với hỗn số dương: $a\frac{b}{c}=\frac{a.c+b}{c}$

Lời giải chi tiết:

Ta có: $-7=\frac{-7}{1}$; $0,5=\frac{5}{10}$; $0=\frac{0}{1}$; $1\frac{2}{3}=\frac{1.3+2}{3}=\frac{5}{3}$.

Chú ý: Ta cũng có thể viết các số trên bằng các phân số khác.

Thực hành 1

Vì sao các số $-0,33;0;3\frac{1}{2};0,25$ là các số hữu tỉ?

Phương pháp giải:

Sử dụng định nghĩa: Số hữu tỉ là các số viết được dưới dạng phân số $\frac{a}{b}$ với $a,b\in Z,b\ne 0.$

Lời giải chi tiết:

Các số $-0,33;0;3\frac{1}{2};0,25$ là các số hữu tỉ vì:

$\begin{array}{c}-0,33=\frac{-33}{100}=\frac{-99}{300}=....\\ 0=\frac{0}{1}=\frac{0}{2}=...\\ 3\frac{1}{2}=\frac{7}{2}=\frac{-7}{-2}=...\\ 0,25=\frac{25}{100}=\frac{1}{4}=...\end{array}$

Vận dụng 1

Viết các số đo các đại lượng sau dưới dạng $\frac{a}{b}$ với $a,b\in Z,b\ne 0.$

a)      $2,5$kg đường

b)      $3,8$ m dưới mực nước biển

Phương pháp giải:

Viết các số thập phân dưới dạng phân số: $a,b=\frac{\overline{ab}}{10}$

Lời giải chi tiết:

a)      $2,5kg=\frac{25}{10}kg=\frac{5}{2}kg$

b)      $3,8m=\frac{38}{10}m=\frac{19}{5}m$

Giải mục 2 trang 6, 7

HĐ 2

a)      So sánh hai phân số $\frac{2}{9}$ và $-\frac{5}{9}$.

b)      Trong mỗi trường hợp sau, nhiệt độ nào cao hơn?

i) $0^{o}C$ và $-0,5^{o}C;$     ii) $-{12}^{o}C$ và $-7^{o}C$.

Phương pháp giải:

a)      Để so sánh hai phân số có cùng mẫu dương ta so sánh hai tử số, tử số nào lớn hơn thì phân số đó lớn hơn.

b)      Số thập phân âm luôn nhỏ hơn $0$.

Để so sánh hai số nguyên âm ta so sánh hai phần tự nhiên của chúng, số nào có phần tự nhiên lớn hơn thì số đó nhỏ hơn.

Lời giải chi tiết:

a)      Ta có: $2>-5$ nên $\frac{2}{9}>\frac{-5}{9}$hay $\frac{2}{9}>-\frac{5}{9}$.

b)      Ta có:

i) $0>-0,5$ nên  $0^{o}C>-0,5^{o}C;$

ii) Do $12>7$ nên $-12<-7$. Do đó, $-{12}^{o}C<-7^{o}C$.

Thực hành 2

Cho các số hữu tỉ: $\frac{-7}{12};\frac{4}{5};5,12;-3;\frac{0}{-3};-3,75.$

a)      So sánh $\frac{-7}{12}$ với $-3,75$; $\frac{0}{-3}$ với $\frac{4}{5}$.

b)      Trong các số hữu tỉ đã cho, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

Phương pháp giải:

a)      Đưa các số hữu tỉ về dạng phân số có mẫu dương rồi so sánh.

b)      So sánh các số hữu tỉ đã cho với số $0$ rồi rút ra kết luận.

Lời giải chi tiết:

a)      +) Ta có: $-3,75=\frac{-375}{100}=\frac{-15}{4}=\frac{-45}{12}$.

Do $-7>-45$ nên $\frac{-7}{12}>\frac{-45}{12}$.

+) Ta có: $\frac{0}{-3}=0$. Nên $\frac{0}{-3}<\frac{4}{5}$.

b)      Các số hữu tỉ dương là: $\frac{4}{5};5,12$.

Các số hữu tỉ âm là: $\frac{-7}{12};-3;-3,75$

Do $\frac{0}{-3}=0$ nên số không là số hữu tỉ dương cũng không là số hữu tỉ âm là: $\frac{0}{-3}$

Phương pháp giải:

a) Vẽ trục số và biểu diễn các điểm.

b) Quan sát Hình 2 và trả lời câu hỏi.

Lời giải chi tiết:

a) 

b) Điểm A biểu diễn số hữu tỉ: $\frac{1}{3}$

1998/Math/MathML">0−3

.

Giải mục 3 trang 7, 8

HĐ 3

a) Biểu diễn các số nguyên -1;1;-2 trên trục số.

b) Quan sát Hình 2. Hãy dự đoán điểm A biểu diễn số hữu tỉ nào?

1111

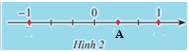
Thực hành 3

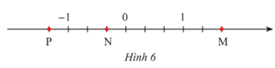
a)      Các điểm M, N, P trong Hình 6 biểu diễn các số hữu tỉ nào?

b)      Biểu diễn các số hữu tỉ sau trên trục số: $-0,75;\frac{1}{-4};1\frac{1}{4}.A17$

 

Phương pháp giải:

a)      Quan sát trục số và trả lời câu hỏi

b)      Các số hữu tỉ âm được biểu diễn bên trái số 0, các số hữu tỉ dương được biểu diễn bên phải số 0.

Lời giải chi tiết:

a)      Các điểm M, N, Q biểu diễn lần lượt các số hữu tỉ:$\frac{5}{3};\frac{-1}{3};\frac{-4}{3}$.

b)       

Giải mục 4 trang 8, 9 

HĐ 4

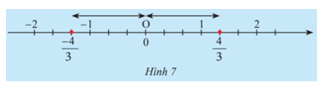
Em có nhận xét gì về vị trí điểm $\frac{-4}{3}$ và $\frac{4}{3}$ trên trục số (Hình 7) so với điểm 0?

Phương pháp giải:

Nhận xét về khoảng cách từ hai điểm trên đến điểm 0.

Lời giải chi tiết:

Hai điểm $\frac{-4}{3}$ và $\frac{4}{3}$ cách đều và nằm về hai phía so với điểm 0.

Thực hành 4

Tìm số đối của mỗi số sau: $7;\frac{-5}{9};-0,75;0;1\frac{2}{3}$.

Phương pháp giải:

Số đối của số hữu tỉ $x$ kí hiệu là $-x$.

Lời giải chi tiết:

Số đối của các số $7;\frac{-5}{9};-0,75;0;1\frac{2}{3}$ lần lượt là: $-7;\frac{5}{9};0,75;0;-1\frac{2}{3}$

Vận dụng 2

Bạn Hồng đã phát biểu: “4,1 lớn hơn 3,5. Vì thế – 4,1 cũng lớn hơn -3,5”.

Theo em, phát biểu của bạn Hồng có đúng không? Tại sao?

Phương pháp giải:

Số hữu tỉ âm nào có phần số dương lớn hơn thì bé hơn.

Lời giải chi tiết:

Do $4,1>3,5$ nên $-4,1<-3,5$. Vì vậy phát biểu của bạn Hồng là sai.

Giải bài 1 trang 9

Đề bài

Thay ? bằng kí hiệu $\in ,\notin$ thích hợp

Phương pháp giải:

Sử dụng định nghĩa các tập hợp số đã học.

Lời giải chi tiết

$\begin{array}{c}-7\notin N;-17\in Z;-38\in Q\\ \frac{4}{5}\notin Z;\frac{4}{5}\in Q;0,25\notin Z;3,25\in Q\end{array}$

Giải bài 2 trang 9

Đề bài

a)      Trong các số sau, những phân số nào biểu diễn số hữu tỉ $\frac{-5}{9}$?

$\frac{-10}{18};\frac{10}{18};\frac{15}{-27};-\frac{20}{36};\frac{-25}{27}.$

Phương pháp giải:

a) - Rút gọn những phân số đã cho

- Chọn những phân số bằng $\frac{-5}{9}$

b) Số đối của $a$ là $-a$

Chú ý: Số đối của 0 là 0

Lời giải chi tiết

a) Ta có:

$\begin{array}{c}\frac{-10}{18}=\frac{-10:2}{18:2}=\frac{-5}{9};\\ \frac{10}{18}=\frac{10:2}{18:2}=\frac{5}{9};\\ \frac{15}{-27}=\frac{15:(-3)}{-27:(-3)}=\frac{-5}{9};\\ -\frac{20}{36}=-\frac{20:4}{36:4}=\frac{-5}{9}.\end{array}$

Vậy những phân số nào biểu diễn số hữu tỉ $\frac{-5}{9}$ là: $\frac{-10}{18};\frac{15}{-27};-\frac{20}{36}.$

b)      Tìm số đối của mỗi số sau: $12;\frac{4}{9};-0,375;\frac{0}{5};-2\frac{2}{5}.$

Phương pháp giải:

a) - Rút gọn những phân số đã cho

- Chọn những phân số bằng $\frac{-5}{9}$

b) Số đối của $a$ là $-a$

Chú ý: Số đối của 0 là 0

Lời giải chi tiết

b) Số đối của các số $12;\frac{4}{9};-0,375;\frac{0}{5};-2\frac{2}{5}$ lần lượt là: $-12;\frac{-4}{9};0,375;\frac{0}{5};2\frac{2}{5}$.

Giải bài 3 trang 9

Đề bài

a)      Các điểm A,B,C trong Hình 8 biểu diễn số hữu tỉ nào?

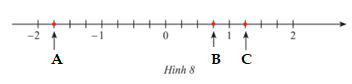
b)      Biểu diễn các số hữu tỉ $\frac{-2}{5};1\frac{1}{5};\frac{3}{5};-0,8$ trên trục số.

Phương pháp giải:

a)      Quan sát Hình 8 và trả lời câu hỏi.

b)      Đưa các số về dạng phân số rồi biểu diễn trên trục số.

Lời giải chi tiết

a)      Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: $\frac{-7}{4};\frac{3}{4};\frac{5}{4}.$

b)      Ta có: $1\frac{1}{5}=\frac{6}{5};-0,8=\frac{-8}{10}=\frac{-4}{5}.$

Vậy ta biểu diễn các số hữu tỉ $\frac{-2}{5};1\frac{1}{5};\frac{3}{5};-0,8$ trên trục số như sau:

Giải bài 4 trang 10

Đề bài

a)      Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

$\frac{5}{12};-\frac{4}{5};2\frac{2}{3};-2;\frac{0}{234};-0,32.$

Phương pháp giải:

a)      So sánh các số đã cho với 0 và kết luận.

b)      So sánh các số rồi sắp xếp các số theo thứ tự từ nhỏ đến lớn

Lời giải chi tiết

a) Các số hữu tỉ dương là: $\frac{5}{12};2\frac{2}{3}.$

Các số hữu tỉ âm là: $-\frac{4}{5};-2;-0,32.$

Số không là số hữu tỉ dương cũng không là số hữu tỉ âm là: $\frac{0}{234}$.

b)      Hãy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn.

Phương pháp giải:

a)      So sánh các số đã cho với 0 và kết luận.

b)      So sánh các số rồi sắp xếp các số theo thứ tự từ nhỏ đến lớn

Lời giải chi tiết

b) Ta có: $-\frac{4}{5}=-0,8$

Vì 0 < 0,32 < 0,8 < 2 nên 0 > -0,32 > -0,8 > -2 hay $-2<-\frac{4}{5}<-0,32<0$

Mà $0<\frac{5}{12}<1;1<2\frac{2}{3}$ nên $0<\frac{5}{12}<2\frac{2}{3}$

Các số theo thứ tự từ nhỏ đến lớn là:

$-2;-\frac{4}{5};-0,32;\frac{0}{234};\frac{5}{12};2\frac{2}{3}$

Chú ý: $\frac{0}{a}=0,a\ne 0.$

Giải bài 5 trang 10

Đề bài

So sánh các cặp số hữu tỉ sau:

a)      $\frac{2}{-5}$ và $\frac{-3}{8}$                

Phương pháp giải:

- Quy đồng hoặc rút gọn để đưa các phân số về cùng mẫu.

- So sánh các phân số cùng mẫu.

Lời giải chi tiết

a)      Ta có: $\frac{2}{-5}=\frac{-16}{40}$ và $\frac{-3}{8}=\frac{-15}{40}$

Do $\frac{-16}{40}<\frac{-15}{40}\Rightarrow \frac{2}{-5}<\frac{-3}{8}$.

b) $-0,85$ và $\frac{-17}{20}$;

Phương pháp giải:

- Quy đồng hoặc rút gọn để đưa các phân số về cùng mẫu.

- So sánh các phân số cùng mẫu.

Lời giải chi tiết

b)      Ta có: $-0,85=\frac{-85}{100}=\frac{-17}{20}$. Vậy $-0,85$=$\frac{-17}{20}$.

c) $\frac{-137}{200}$  và $\frac{37}{-25}$         

Phương pháp giải:

- Quy đồng hoặc rút gọn để đưa các phân số về cùng mẫu.

- So sánh các phân số cùng mẫu.

Lời giải chi tiết

c)      Ta có: $\frac{37}{-25}=\frac{-296}{200}$  

Do  $\frac{-137}{200}>\frac{-296}{200}$ nên $\frac{-137}{200}$ > $\frac{37}{-25}$ .

d) $-1\frac{3}{10}$ và $-\left(\frac{-13}{-10}\right)$.

Phương pháp giải:

- Quy đồng hoặc rút gọn để đưa các phân số về cùng mẫu.

- So sánh các phân số cùng mẫu.

Lời giải chi tiết

d)      Ta có: $-1\frac{3}{10}=\frac{-13}{10}$ ;

$-\left(\frac{-13}{-10}\right)=\frac{-13}{10}$.

Vậy $-1\frac{3}{10}=-\left(\frac{-13}{-10}\right)$.

Giải bài 6 trang 10

Đề bài

So sánh các cặp số hữu tỉ sau:

a) $\frac{-2}{3}$ và $\frac{1}{200}$;          

Phương pháp giải:

So sánh các cặp phân số với số thứ ba.

Lời giải chi tiết

a)      Ta có $\frac{-2}{3}<0$ và $\frac{1}{200}>0$ nên $\frac{-2}{3}$<$\frac{1}{200}$.

b) $\frac{139}{138}$ và $\frac{1375}{1376}$;      

Phương pháp giải:

So sánh các cặp phân số với số thứ ba.

Lời giải chi tiết

b)      Ta có: $\frac{139}{138}>1$ và $\frac{1375}{1376}<1$ nên $\frac{139}{138}$ > $\frac{1375}{1376}$.

c) $\frac{-11}{33}$ và $\frac{25}{-76}$.

Phương pháp giải:

So sánh các cặp phân số với số thứ ba.

Lời giải chi tiết

c)      Ta có: $\frac{-11}{33}=\frac{-1}{3}$ và $\frac{25}{-76}=\frac{-25}{76}>\frac{-25}{75}=\frac{-1}{3}\Rightarrow \frac{25}{-76}>\frac{-11}{33}$.

Giải bài 7 trang 10

Đề bài

Bảng dưới đây cho biết độ cao của bốn rãnh đại dương so với mực nước biển.

a) Những rãnh đại dương nào có độ cao cao hơn rãnh Puerto Rico? Giải thích.

Phương pháp giải:

a)      So sánh các độ cao với rãnh Puerto Rico

b)      So sánh các độ cao các rãnh đại dương và kết luận rãnh có độ cao thấp nhất.

Lời giải chi tiết

Ta có: $-10,5<-8,6<-8,0<-7,7$.

Vậy ta có thứ tự các độ cao từ thấp đến cao là: Rãnh Philippine, rãnh Puerto Rico, rãnh Peru-Chile, rãnh Romanche.

a)      Những rãnh có độ cao cao hơn rãnh Puerto Rico là: rãnh Peru-Chile, rãnh Romanche vì -7,7 > -8,0 > -8,6

b) Rãnh đại dương nào có độ cao thấp nhất trong bốn rãnh trên? Giải thích.

Phương pháp giải:

a)      So sánh các độ cao với rãnh Puerto Rico

b)      So sánh các độ cao các rãnh đại dương và kết luận rãnh có độ cao thấp nhất.

Lời giải chi tiết

Ta có: $-10,5<-8,6<-8,0<-7,7$.

Vậy ta có thứ tự các độ cao từ thấp đến cao là: Rãnh Philippine, rãnh Puerto Rico, rãnh Peru-Chile, rãnh Romanche.

b)      Rãnh đại dương nào có độ cao thấp nhất trong bốn rãnh trên là: rãnh Philippine vì - 10,5 <  - 8,6 <  - 8,0 <  - 7,7

So sánh các cặp số hữu tỉ sau:

a) $\frac{-2}{3}$ và $\frac{1}{200}$;          

Phương pháp giải:

So sánh các cặp phân số với số thứ ba.

Lời giải chi tiết

a)      Ta có $\frac{-2}{3}<0$ và $\frac{1}{200}>0$ nên $\frac{-2}{3}$<$\frac{1}{200}$.

b) $\frac{139}{138}$ và $\frac{1375}{1376}$;      

Phương pháp giải:

So sánh các cặp phân số với số thứ ba.

Lời giải chi tiết

b)      Ta có: $\frac{139}{138}>1$ và $\frac{1375}{1376}<1$ nên $\frac{139}{138}$ > $\frac{1375}{1376}$.

c) $\frac{-11}{33}$ và $\frac{25}{-76}$.

Phương pháp giải:

So sánh các cặp phân số với số thứ ba.

Lời giải chi tiết

c)      Ta có: $\frac{-11}{33}=\frac{-1}{3}$ và $\frac{25}{-76}=\frac{-25}{76}>\frac{-25}{75}=\frac{-1}{3}\Rightarrow \frac{25}{-76}>\frac{-11}{33}$.