Giải các bài toán điển hình lớp 4 bằng phương pháp dùng sơ đồ đoạn thẳng.
- Họ và tên: Phan Thị Thu Hoa
- Ngày tháng năm sinh: Ngày
27/08/1964
- Năm vào ngành: 09/1984
- Chức vụ: Giáo viên
- Đơn vị công tác: Giáo viên trường
tiểu học Trung Hoà - Cầu Giấy – Hà Nội.
- Trình độ chuyên môn: Cao Đẳng
sư phạm
- Khen thưởng: Nhiều năm liên tục
là giáo viên giỏi cấp Quận.3
I. Lý do chọn đề tài
Cùng với Tiếng Việt – Toán học là
môn học có vị trí và vai trò vô cùng quan trọng ở bậc tiểu học. Toán học giúp bồi
dưỡng tư duy lô gíc, bồi dưỡng và phát sinh phương pháp suy luận, phát triển
trí thông minh, tư suy lô gíc sáng tạo, tính chính xác, kiên trì, trung thực.
Việc giải toán điển hình bằng
phương pháp dùng cơ sở đoạn thẳng là rất quan trọng vì “Sơ đồ đoạn thẳng” là một
phương tiện trực quan được sử dụng trong việc dạy, giải toán ngay từ lớp 1 bởi
nó đáp ứng được nhu cầu tăng dần mức độ trừu tượng trong việc cung cấp các kiến
thức toán học cho học sinh.
Phương tiện trực quan thì có nhiều
nhưng qua thực tế giảng dạy tôi nhận thấy sơ đồ đoạn thẳng là phương tiện cần
thiết, quan trọng và hết sức hữu hiệu trong việc dạy giải toán (Một kỹ năng cần
thiết nhất) ở bậc tiểu học nói chung và ở các lớp cuối cấp nói riêng. Trong phạm
vi đề tài này tôi xin đề cập đến vấn đề “ứng dụng phương pháp giải toán điển
hình”.
Để giúp học sinh có kỹ năng giải
toán nói chung và kỹ năng giải bằng phương pháp dùng sơ đồ đoạn thẳng nói
riêng. Tôi đã giúp cho học sinh nắm một số bước cơ bản sau đây:
II. Các bước cơ bản để giải một bài toán bằng
“Phương pháp dùng sơ đồ đoạn thẳng”
Bước 1: Tìm hiểu đề bài
Sau khi phân tích đề toán, suy
nghĩ về ý nghĩa Bài toán , nội dung Bài toán đặc biệt chú ý đến câu hỏi của Bài
toán .
Bước 2: Lập luận để vẽ sơ đồ
Sau khi phân tích đề, thiết lập
được mối quan hệ và phụ thuộc giữa các đại lượng cho trong Bài toán đó. Muốn
làm việc này ta thường dùng sơ đồ đoạn thẳng thay cho các số (số đã cho, số phải
tìm trong Bài toán ) để minh hoạ các quan hệ đó.
Khi vẽ sơ đồ phải chọn độ dài các
đoạn thẳng và sắp xếp các đoạn thẳng đó một cách thích hợp để có thể dễ dàng thấy
được mối quan hệ phụ thuộc giữa các đại lượng, tạo ra một hình ảnh cụ thể giúp
ta suy nghĩ tìm tòi cách giải một Bài toán .
Có thể nói đây là một bước quan
trọng vì đề toán được làm sảng tỏ: mối quan hệ giữa các đại lượng trong Bài toán
được nêu bật các yếu tố không cần thiết được lược bỏ.
Để có thể thực hiện những Bài toán
bằng sơ đồ đoạn thẳng thì nắm được cách biểu thị các phép tính (cộng, trừ,
nhân, chia) các mối quan hệ (quan hệ về hiệu, quan hệ về tỷ số) là hết sức quan
trọng. Vì nó làm một công cụ biểu đạt mối quan hệ và phụ thuộc giữa các đại lượng.
“Công cụ” này học sinh đã được trang bị từ những lớp đầu cấp nhưng cần được tiếp
tục củng cố, “mài giũa” ở các lớp cuối cấp.
Bước 3: Lập kế hoạch giải toán
Dựa vào sơ đồ suy nghĩ xem từ các
số đã cho và điều kiện của Bài toán có thể biết gì? có thể làm gì? phép tính đó
có thể giúp ta trả lời câu hỏi của Bài toán không? trên có sở đó, suy nghĩ để
thiết lập trình tự giải Bài toán .
Bước 4: Giải và kiểm tra các bước giải
+ Thực hiện các phép tính theo
trình tự đã thiết lập để tìm ra đáp số
+ Mỗi khi thực hiện phép tính cần
kiểm tra xem đã đúng chưa? Giải xong Bài toán phải thử xem đáp số đã tìm được
có trả lời đúng câu hỏi của Bài toán có phù hợp với các điều kiện của bải toán
không.
Tóm lại, để học sinh có thể sử dụng
thành thạo “phương pháp dùng sơ đồ đoạn thẳng” trong việc giải toán thì việc
giúp cho các em hiểu rõ ý nghĩa của từng dạng toán sau đó có thể mô hình hoá nội
dung từng dạng bằng sơ đồ đoạn thẳng từ đó tìm ra cách giải Bài toán là một việc
làm hết sức quan trọng. Làm được việc này giáo viên đã đạt được mục tiêu lớn nhất
trong giảng dạy đó là việc không chỉ dừng lại ở việc “dạy toán” mà còn hướng dẫn
học sinh “học toán sao cho đạt hiệu quả cao nhất”.
Để khẳng định cụ thể hơn lợi ích
của việc sử dụng sơ đồ đoạn thẳng để dạy giải toán ở tiểu học tôi xin trình bày
một số dạng toán cơ bản mà khi giải có thể sử dụng sơ đồ đoạn thẳng.
Dạng 1: Dạng toán có liên quan đến số trung bình cộng
Đối với dạng toán này, học sinh nắm
được khái niệm số trung bình cộng.
Biết cách tìm số trung bình cộng
của nhiều số. Khi giải các Bài toán dạng này, thông thường các em thường sử dụng
công thức.
Số trung bình = Tổng : số các số
hạng
1. Tổng = số trung bình cộng x số
các số hạng
2. Số các số hạng = tổng : số
trung bình cộng áp dụng kiến thức cơ bản đó học sinh được làm quen với rất nhiều
dạng toán về trung bình cộng mà có những Bài toán nếu không tóm tắt bằng sơ đồ,
học sinh sẽ rất khó khăn trong việc suy luận tìm ra cách giải.
Ví dụ: An có 20 nhãn vở, Bình có
số nhãn vở bằng An. Chi có số nhẵn vở ít hơn trung bình cộng số nhãn vở của 3 bạn
là 6 nhãn vở. Hỏi chi có bao nhiêu nhãn vở?
Sau khi đọc kỹ đề toán, phân tích
mối quan hệ giữa các đại lượng trong bài, học sinh tóm tắt Bài toán bằng sơ đồ:
+ Trước hết vẽ đoạn thẳng:
Biểu thị tổng số nhẵn vở của 3 bạn
+ Dựa vào đó học sinh nêu cách vẽ
đoạn thẳng thể hiện mức trung bình cộng số nhãn vở của 3 bạn (1/3 tổng trên)
+ Từ đó vẽ đoạn thẳng biểu thị số
nhãn vở của Chi (ít hơn mức trung bình cộng là 6 chiếc).
Sau khi hướng dẫn tìm hiểu đề và
tóm tắt bằng sơ đồ, nhiều học sinh đã biết từng bước tìm cách giải. Những em
chưa làm được bài, sau khi nghe bạn trình bày cách suy luận của sơ đồ các em đều
nắm được và bết tự giải quyết các Bài toán dạng tương tự.
Số nhãn vở của An và Bình là:
20 + 20 = 40 (nhãn vở)
Nhìn vào sơ đồ ta thấy, trung
bình cộng số nhãn vở của 3 bạn là
(40 – 6) : 2 = 17 (nhãn vở)
Bạn Chi có số nhãn vở là:
17 – 6 = 11 (nhãn vở)
Đáp số: 11 nhãn vở
Ví dụ 2:
Dùng sơ có thể giúp học sinh hiểu
hoặc các em có thể giải thích cách làm dạng toán tìm 2 số khi biết hiệu và
trung bình cộng của 2 số đó một cách ngắn gọn.
Qua sơ đồ ta có thể tìm ra:
Số lớn = trung bình cộng + (hiệu
: 2)
Số bé = Trung bình cộng – (Hiệu
:8
Ví dụ một Bài toán cụ thể dạng
này:
Trung bình cộng của 2 số tròn chục
liên tiếp là 2005. Tìm hai số đó.
Vì hai số tròn chục liên tiếp kém
nhau 10 đơn vị nên ta có sơ đồ:

Trung bình cộng của 2 số tròn chục liên tiếp là 2005. Tìm hai số đó.
Vì hai số tròn chục liên tiếp kém nhau 10 đơn vị nên ta có sơ đồ:
Bài giải:
Số lớn là:
2005 + (10 : 2) = 2010
Số bé là:
2005 – (10 : 2) = 2000
Hoặc 2010 – 10 = 2000
Đáp số: Số lớn 2010
Số bé 20009
Ví dụ 3:
Một tổ công nhân đường sắt sửa đường,
ngày thứ nhất sửa được 15m đường, ngày thứ 2 sửa được nhiều hơn ngày thứ nhất
1m, ngày thứ 3 sửa được nhiều hơn ngày thứ nhất 2m. Hỏi trung bình mỗi ngày sửa
được bao nhiêu mét đường?
Ta có sơ đồ:
Thông thường ta giải bài toán như
sau:
Ngày thứ hai sửa được là:
15 + 1 = 16 (m)
Ngày thứ 3 sửa được
15 + 2 = 17 (m)
Trung bình mỗi ngày sửa được
(15 + 16 + 17) : 3 = 16 (m)
Đáp số: 16 (m)10
Nhận xét: Quan sát kỹ sơ đồ ta thấy
nếu chuyển một mét từ ngày thứ 3 sang ngày thứ nhất thì số m đường sửa được
trong các ngày đều bằng 16m.
Ta thấy ngay trung bình mỗi ngày
tổ đó sửa được 16m đường.
Như vậy, sơ đồ giúp ta hình dung
rõ khái niệm, đôi khi sơ đồ còn giúp ta tính nhẩm nhanh kết quả.
Dạng 2: Dạng toán tìm hai số khi biết tổng và hiệu của chúng.
Bài toán : Tổng hai số là 48, hiệu
hai số là 12. Tìm hai số đó?
Tóm tắt Bài toán bằng sơ đồ, căn
cứ sơ đồ hướng dẫn học sinh tìm ra phương pháp giải.
Sử dụng sơ đồ biểu thị mối quan hệ
về hiệu, các em sẽ tóm tắt Bài toán bằng sơ đồ dưới đây.
Nhìn vào sơ đồ, yêu cầu học sinh
nhận xét:
+ Nếu lấy tổng trừ đi hiệu, kết
quả đó có quan hệ như thế nào với số bé?
(Giáo viên thao tác che phần hiệu
là 12 trên sơ đồ)... từ đó học sinh sẽ dễ dàng nhận thấy phần còn lại là 2 lần
số bé.
Dựa vào suy luận trên, yêu cầu học
sinh nêu cách tìm số bé.
Hơn 80% số em nêu được tìm số bé
là:
(42 – 12) : 2 = 18
Tìm được số bé suy ra số lớn là:
18 + 12 = 30
Hay: 48 – 18 = 30
Từ bài toán ta xây dựng được công
thức tính:
Cách giải vừa nêu trên là dễ nhất
với học sinh. Tuy nhiên cũng có thể giới thiệu thêm phương pháp sau đây:
Cũng biểu thị mối quan hệ hiệu
nhưng sử dụng sơ đồ
Suy luận: nếu thêm một đoạn thẳng
hiệu (12) vào số bé ta được hai đoạn thẳng bằng nhau tức là hai lần số lớn.
Từ đó suy ra:
Số lớn là:
(48 + 12) : 2 = 30
Vậy số bé là: 30 – 12 = 18
Hoặc: 48 – 30 = 18
Sau khi học sinh đã nắm được cách
giải ta xây dựng công thức tổng quát:
Như vậy qua sơ đồ đoạn thẳng học
sinh nắm được phương pháp giải dạng toán này và có thể áp dụng để giải các bài tập
về tìm hai số khi biết tổng và hiệu ở nhiều dạng khác nhau.
Ví dụ 1:
Ba lớp A, B, C mua tất cả 120 quyển
vở. Tính số vở của mỗi lớp biết rằng nếu lớp 4A chuyển cho lớp 4B 10 quyển và
cho lớp 4C 5 quyển thì số vở của 3 lớp sẽ bằng nhau:
Phân tích nội dung Bài toán sẽ vẽ
được sơ đồ
Dựa vào sơ đồ ta có:
Sau khi lớp 4A chuyển cho hai lớp
thì mỗi lớp có số vở là:
120:3 = 40 (quyển)
Lúc đầu lớp 4C có là:
40-5 = 35 (quyển)
Lúc đầu lớp 4B có là:
40-10 = 30 (quyển)
Lúc đầu lớp 4A có là:
40 + 10 + 5 = 55 (quyển)
ĐS: 4A: 55 quyển; 4B: 30 quyển;
4C: 35 quyển
Dạng 3: Tìm hai số khi biết tổng và tỉ của chúng
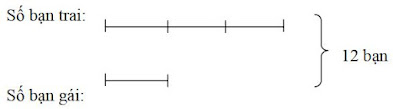
Bài toán : Một đội tuyển học sinh
giỏi toán có 12 bạn, trong đó số bạn gái bằng 1/3 số bạn trai. Hỏi có mấy bạn
gái, mấy bạn trai trong đội tuyển đó?
Tóm tắt Bài toán bằng sơ đồ, cắn
cứ vào sơ đồ hướng dẫn học sinh tìm raphương pháp giải:
Sử dụng sơ đồ biểu thị mối quan hệ
về tỷ số và các em sẽ tóm tắt Bài toán bằng sơ đồ dưới đây:
Vẽ sơ đồ đoạn thẳng thế này học
sinh dễ dàng thấy được hai điều kiện của Bài toán : cả trai và gái có 12 bạn
(biểu thị mối quan hệ về tổng) và có số bạn trai gấp 3 lần số bạn gái (biểu thị
mối quan hệ về tỷ).
Sơ đồ trên gợi cho ta cách tìm số
bạn gái bằng cách lấy 12 chia cho 3 + 1 = 4 (vì số bạn gái ứng với 1/4 tổng số
bạn).
Cũng dựa vào sơ đồ ta dễ dàng tìm
được số bạn trai
Bài giải
Tổng số phần bằng nhau là
1 + 3 = 4 (phần)
Số bạn gái trong đội tuyển là
12 : 4 = 3 (bạn)
Số bạn trai trong đội tuyển là
3 x 3 = 9 (bạn)
Hoặc 12 – 3 = 9 (bạn)
Đáp số: Trai: 9 bạn15
Giái: 3 bạn
Từ bài toán cơ bản trên ta xây dụng
quy tắc giải Bài toán tìm hai số khi biết tổng và tỷ số của 2 số đó.
Nắm được quy tắc giải học sinh sẽ
biết áp dụng để giải nhiều Bài toán cùng dạng, học sinh giỏi sẽ biết áp dụng
quy tắc để giải các Bài toán khó dạng này (đó là các Bài toán cùng dạng như tổng,
tỷ được thể hiện dưới dạng ẩn).
Ví dụ 1:
Hai đội xanh và đỏ có tất cả 45
quả bóng. Tính xem mỗi đội có bao nhiêu quả bóng. Biết 3 lần số bóng đội xanh bằng
2 lần số bóng đội đỏ.
Bước 1: Ta vẽ sơ đồ biểu thị 3 lần số bóng đội xanh = 2 lần số bóng
đội đỏ. 2 lần đội đỏ:
Bước 1: Vẽ sơ đồ
Bước 2: Tìm tổng số phần bằng nhau
Bước 3: Tìm giá trị một phần
Giá trị một phần = Tổng : Tổng số
phần bằng nhau
Bước 4: Tìm số bé
Số bé = giá trị 1 phần x số phần
của số bé
Bước 5: Tìm số lớn
Số lớn = giá trị 1 phần x số phần
của số lớn
Hoặc = tổng – số bé 3 lần đội
xanh:
Nắm được quy tắc giải học sinh sẽ biết áp dụng để giải nhiều bài toán cùng
dạng, học sinh giỏi sẽ biết áp dụng quy tắc để giải các bài toán khó dạng này (đó là
các bài toán cùng dạng như tổng, tỷ được thể hiện dưới dạng ẩn).
Ví dụ 1:
Hai đội xanh và đỏ có tất cả 45 quả bóng. Tính xem mỗi đội có bao nhiêu
quả bóng. Biết 3 lần số bóng đội xanh bằng 2 lần số bóng đội đỏ.
Bước 1: Ta vẽ sơ đồ biểu thị 3 lần số bóng đội xanh = 2 lần số bóng đội đỏ
Nhìn vào sơ đồ ta thấy nếu chia số
bóng của đội xanh thành 2 phần và chia số bóng của đội đỏ thành 3 phần thì các
phần sẽ bằng nhau. Với tỷ số bóng 2 đội là
2/3. Ta có sơ đồ biểu thị số bóng của 2 đội.
Bài giải
Tổng số phần bằng nhau là
2 + 3 = 5 (phần)
Số bóng ứng với một phần là
45 : 5 = 9 (quả)
Số bóng đội xanh là
9 x 2 = 18 (quả)
Số bóng đội đỏ là
9 x 3 = 27 (quả)
Đáp số: Đội xanh: 18 quả17
Đội đỏ: 27 quả
Ví dụ 2: Tổng số tuổi của 2 anh
em hiện nay là 25 tuổi. Trước đây khi anh bằng tuổi em hiện nay thì tuổi anh gấp
hai lần tuổi em. Tính tuổi của mỗi người hiện nay?
Đây thực sự là Bài toán về tìm 2
số khi biêt tổng và tỷ số nhưng không ở dạng cơ bản mà đã được nâng cao lên bằng
cách diễn đạt tỷ số dưới dạng ẩn. Vì vậy khi nhận được đề bài này học sinh rất
lúng túng khi xác định được cách giải đúng. Sau khi gợi ý, phân tích và hướng dẫn
từng bước sơ đồ hoá nội dung Bài toán các em nhận ra ngay dạng toán quen thuộc
tìm hai số khi biết tổng bà tỷ số.
+ Trước hết yêu cầu học sinh vẽ
sơ đồ biểu thị số tuổi của 2 anh em trước đây.
Nhận xét: Hiệu số tuổi của hai
anh em là 1 “phần”. Hiệu số phần bằng nhau giữa tuổi anh và tuổi em không thay
đổi theo thời gian (vì sau cùng một số năm thì 2 anh em cùng tăng một số tuổi
như nhau). Như vậy tuổi anh hiện nay bằng 3 lần tuổi em trước đây.
Ta có sơ đồ:
Dùng phương pháp giải Bài toán tìm
hai số khi biết tổng và tỷ số của 2 số đó học sinh đễ dàng tìm ra đáp số bài toán
.
TK: Qua các ví dụ trên ta có thể
thấy sơ đồ đoạn thẳng không chỉ đơn thuần dùng để tóm tắt Bài toán mà còn là một
công cụ giúp cho việc suy luận tìm ra cách giải toán. Sử dụng sơ đồ ta có thể
làm cho các Bài toán khó, phức tạp trở thành các Bài toán đơn giản theo dạng cơ
bản nên có thể dễ dàng giải được.
Dạng 4: Tìm hai số khi biết hiệu và tỷ của chúng
Bài toán : Tim hai số tự nhiên biết
hiệu của chúng là 27 và số này bằng 2/5 số kia.
Học sinh phân tích để vẽ sơ đồ vừa
biểu thị mối quan hệ về hiệu, vừa biểu thị mối quan hệ về tỷ số:
Dựa vào sơ đồ tiến hành tương tự
như khi dạy dạng toán “Tìm hai số khi biết tổng và tỷ số của hai số đó”. Học
sinh tìm ra cách giải Bài toán .
Tổng kết thành quy tắc giải dạng
toán tìm hai số khi biết hiệu và tỷ số của hai số đó.
Bước 1: Vẽ sơ đồ
Bước 2: Tìm hiệu số phần bằng nhau
Bước 3: Tìm giá trị một phần
Giá trị một phần = Hiệu : Hiệu số
phần bằng nhau
Bước 4: Tìm số bé
Số bé = giá trị 1 phần x số phần
của số bé
Bước 5: Tìm số lớn
Số lớn = giá trị 1 phần x số phần
của số lớn
Hoặc = Số bé + hiệu19
Nắm vững quy tắc giải học sinh
cũng sẽ biết áp dụng để giải các Bài toán nâng cao.
Việc dùng sơ đồ đoạn thẳng một lần
nữa lại thể hiện vai trò vô cùng quan trọng vì sơ đồ chính là chỗ dựa giúp học
sinh dễ dàng trong việc suy luận tìm ra cách giải. Ta có thể lấy một số Bài toán
sau đây làm ví dụ.
Ví dụ 1: Hiệu hai số là 7, nếu gấp số thứ nhất lên 5 lần và giữ
nguyên số thứ 2 thì hiệu mới là 29. Tìm hai số đó?
Hướng dẫn học sinh sơ đồ hoá nội
dung Bài toán như sau:
Trước hết vẽ hai đoạn thẳng biểu
thị hai số mà hiệu của chúng là 7
Tiếp theo kéo dài đoạn thẳng biểu
thị số thứ nhất để hiển thị số đó được gấp lên 5 lần.
Yêu cầu học sinh xác định trên sơ
đồ đoạn thẳng chỉ hiệu mới
Sơ đồ bài toán
Với sơ đồ trên học sinh có thể thấy
ngay
Bốn lần số thứ nhất là:
39 – 7 = 32
Số thứ nhất là:
32 : 4 = 8
Số thứ hai là:
8 – 7 = 1
Vậy hai số đó là 8 và 1
Ví dụ 3: Hiện nay cha gấp 4 lần
tuổi con. Trước đây 6 năm tuổi cha gấp 13 lần tuổi con. Tính tuổi cha và tuổi
con hiện nay?
Đây là một Bài toán khó, học sinh
sẽ lúng túng vì cả hiệu và tỷ số đều dưới dạng ẩn. Nhưng sử dụng sơ đồ đoạn thẳng
các em sẽ có số dựa vào suy luận và đưa ra Bài toán về dạng điển hình.
Sơ đồ bài toán :
Theo sơ đồ, hiệu số tuổi của cha
và con bằng 12 lần tuổi con lúc đó.
Còn hiệu số tuổi của cha và con
hiện nay bằng 3 lần tuổi con hiện nay.
Vì hiện nay không thay đổi nên 3
lần tuổi con hiện nay bằng 12 lần tuổi con trước đây.
Ta vẽ sơ đồ biểu thị tuổi con trước
đây và tuổi con hiện nay:
Bài toán được đưa ra dạng cơ bản
học sinh dễ dàng giải được:
Giải
Từ sơ đồ suy ra tuổi con trước
đây là:
6 : (4 – 1) = 2(tuổi)
Tuổi con hiện nay là:
2 + 6 = 8 (tuổi)
Tuổi cha hiện nay là:
4 x8 = 32 (tuổi)
Đáp số: Cha: 32 tuổi
Con: 8 tuổi
III. Kết quả
Thực tế giảng dạy ở trường tiểu học
tôi nhận thấy việc sử dụng sơ đồ đoạn thẳng trong dạy toán điển hình hết sức cần
thiết và có hiệu quả cao. Sau quá trình thực hiện đề tài kết quả bài kiểm tra về
giải toán về điển hình cao hơn và kết quả học tập môn toán của học sinh cũng
nâng cao rõ rệt.
IV. Bài học kinh nghiệm
Để giúp học sinh có được kỹ năng
sử dụng sơ đồ đoạn thẳng để giải các Bài toán điển hình tôi đã chú ý các bước
sau:
- Tìm hiểu đề bài
- Lập luận để vẽ sơ đồ
- Lập kế hoạch giải toán
- Giải và kiểm tra các bước giải
V. Kết luận
Để việc sử dụng sơ đồ có hiệu quả
tôi nhận thấy giáo viên phải nắm được trình độ học sinh của mình để lựa chọn
phương pháp và hình thức tổ chức cho phù hợp tạo ra không khí vui vẻ, sôi nổi.
Học sinh, tìm tòi phát hiện kiến thức, giáo viên chỉ đạo.
Khi dạy mỗi bài, mỗi dạng cần
giúp em nắm vững bản chất, xác lập mối quan hệ giữa các dữ kiện, không bỏ sót dữ
kiện để có kỹ năng giải thạo.
Việc vận dụng một cách khéo léo
phương pháp trực quan bằng sơ đồ đoạn thẳng là việc dạy học toán không chỉ đem
lại cho học sinh những tri thức mới, những kỹ năng cơ bản cần thiết của việc giải
toán mà nó còn góp phần hình thành phương pháp học tập, phương pháp phát hiện
và giải quyết các vấn đề trong học tập và cuộc sống.
Trên đây là một số ý kiến, kinh
nghiệm trong việc giảng dạy của tôi. Rât mong được sự góp ý của các cấp lãnh đạo,
của các bạn đồng nghiệp giúp tôi tiếp tục nâng cao trình độ chuyên môn nghiệp vụ.
Hà Nội, ngày 20 tháng 02 năm 2008
ý kiến đánh giá xếp loại của hội
đồng khoa học cơ sở
Người viết SKKN
Phan Thị Thu Hoa





















0 Comments:
Đăng nhận xét