Bài tập cuối chương 3. HÌNH HỌC TRỰC QUAN. CÁC HÌNH PHẲNG TRONG THỰC TIỄN

 

Giải bài 1 trang 76 Sách bài tậpToán 6 – Chân trời sáng tạo

Đề bài

Cho hình vuông ABCD có AB = 9 cm. Tính độ dài các đoạn thẳng DC và AD.

Lời giải chi tiết

Vì ABCD là hình vuông nên AB = AD = DC = 9 cm.

Giải bài 2 trang 76 Sách bài tậpToán 6 – Chân trời sáng tạo

Đề bài

Dùng thước và eke để vẽ hình vuông có độ dài cạnh 7 cm. Hãy dùng compa so sánh đường chèo của hình vuông đó.

Lời giải chi tiết

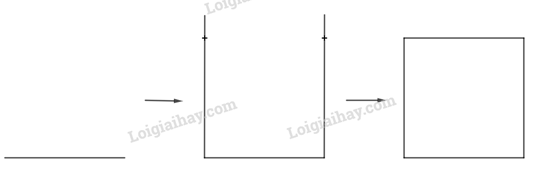
- Dùng thước vẽ đoạn thẳng AB = 7 cm

- Dùng eke và thước vẽ các đường thẳng vuông góc với AB tại A và B.

- Trên đường vuông góc tại A lấy điểm D với AD = 7 cm. Trên đường vuông góc tại B lấy điểm C với BC = 7 cm.

- Kẻ đoạn thẳng nối C và D ta được tứ giác ABCD là hình vuông có độ dài cạnh 7 cm

Nối 2 đường chéo AC và BD. Dùng comp so sánh 2 bán kính lần lượt là AC và BD dễ dàng suy ra hai đường chéo này bằng nhau.

Giải bài 3 trang 76 Sách bài tậpToán 6 – Chân trời sáng tạo

Đề bài

Cho tam giác đều DEF có DE = 5 cm. Tính độ dài các cạnh EF, DF.

Lời giải chi tiết

Tam giác DEF đều nên EF = DF = DE = 5 cm.

Giải bài 4 trang 76 Sách bài tập Toán 6 – Chân trời sáng tạo

Đề bài

Dùng thước và compa để vẽ tam giác đều có độ dài cạnh 3 cm.

Lời giải chi tiết

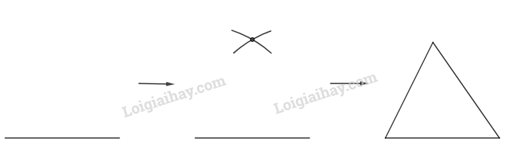
- Dùng thước vẽ đoạn thẳng AB = 3cm

- Dùng compa vẽ các phần đường tròn cùng bán kính 3cm và có tâm lần lượt là A, B.

- Hai phần đường tròn nói trên cắt nhau tại điểm C.

- Kẻ đoạn thẳng nối C và A, C và B ta có tam giác đều ABC với cạnh 3cm.

Giải bài 5 trang 77 Sách bài tập Toán 6 – Chân trời sáng tạo

Đề bài

Cho lục giác đều ABCDEF với cạnh AB = 8 cm và đường chéo AD = 16 cm. Tính độ dài các đoạn thẳng CD và CF.

Phương pháp giải - Xem chi tiết

Lục giác đều có 6 cạnh bằng nhau, các đường chéo chính bằng nhau.

Lời giải chi tiết

Vì ABCDEF là lục giác đều nên AB = CD = 8 cm và AD = CF = 16 cm.

Giải bài 6 trang 77 Sách bài tậpToán 6 – Chân trời sáng tạo

Đề bài

Cho hình chữ nhật ABCD có AB = 12 cm, BC = 9 cm, BD = 15 cm. Tính độ dài của AD, CD, AC.

Lời giải chi tiết

Vì ABCD là hình chữ nhật nên :

$\{\begin{array}{c}AB=CD\\ AD=BC\\ AC=BD\end{array}\Rightarrow \{\begin{array}{c}CD=12cm\\ AD=9cm\\ AC=15cm\end{array}$

Giải bài 7 trang 77 Sách bài tậpToán 6 – Chân trời sáng tạo

Đề bài

Cho hình thoi ABCD với O là giao điểm  của hai đường chéo. Biết AB = 20 cm, OA = 16 cm, OB = 12 cm. Tính độ dài các cạnh và các đường chéo của hình thoi.

Phương pháp giải - Xem chi tiết

ABCD là hình thoi nên có 4 cạnh bằng nhau tức là: AB = BC = CD = DA = 20 cm.

Đường chéo AC = 2. OA = 2. 16 = 32 (cm) và BD = 2.OB = 2.12 = 24 (cm)

Giải bài 8 trang 77 Sách bài tậpToán 6 – Chân trời sáng tạo

Đề bài

Cho hình bình hành ABCD có O là giao điểm của hai đường chéo và thỏa mãn AB = 16 cm, AD = 10 cm, OC = 6 cm. Tính độ dài của CD, BC, AC.

Lời giải chi tiết

Vì ABCD là hình bình hành nên CD = AB = 16 cm; BC = AD = 10 cm và AC = 2.O  =2.6 = 12 cm.

Giải bài 9 trang 77 Sách bài tậpToán 6 – Chân trời sáng tạo

Đề bài

Cho hình thang cân MNPQ với cạnh đáy là MN và PQ, PN = 6 cm, PM = 10 cm. Tính MQ, NQ.

Lời giải chi tiết

Vì MNPQ là hình thang cân nên MQ = NP = 6 cm và NQ = MP = 10 cm.

Giải bài 10 trang 77 sách bài tập Toán 6 – Chân trời sáng tạo

Đề bài

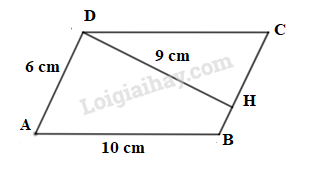
Tính chu vi và diện tích của hình bình hành ABCD (như hình bên). Biết rằng AD = 6 cm; AB = 10 cm, DH = 9cm.

Phương pháp giải - Xem chi tiết

Chu vi hình bình hành ABCD là: C = 2. (AB + AD)

Lời giải chi tiết

Chu vi hình bình hành là: 2. (AB + AD) = 2. (10 + 6) = 32 (cm)

Coi hai đáy của hình bình hành là AD và BC thì chiều cao tương ứng là DH, vậy diện tích của hình bình hành là: AD.DH = 6. 9 = 54 ($c{m}^2$)

Giải bài 11 trang 77 Sách bài tậpToán 6 – Chân trời sáng tạo

Đề bài

Tính chu vi và diện tích của Hình 1 và tính diện tích của Hình 2 sau đây.

Lời giải chi tiết

Hình 1:

Chu vi hình 1 là:

25 + 50 +50 + 55 = 180 (m)

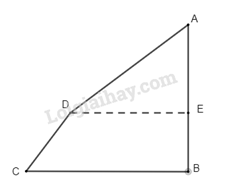
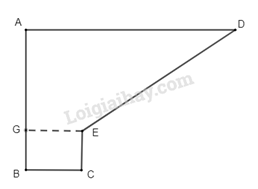
Chia hình 1 thành hình gồm 1 tam giác và 1 hình thang cân như hình dưới.

Ta có: AD = 50 m, AB = 50 m, CD = 25 m, BC = 55 m.

Từ đề bài dễ dàng suy ra BE = 20 m và DE = 40m.

$\Rightarrow$AE = AB – BE = 50 – 20 = 30 (m)

Diện tích tam giác ADE là: ED. AE : 2 = 40 . 30 : 2 = 600 ($m^2$)

Diện thích hình thang CDEB là: (DE+BC).BE:2 = (40 + 55). 20 : 2 = 950 ($m^2$)

Vậy diện tích Hình 1 là: 600 + 950 = 1550 ($m^2$)

Hình 2:

Ta chia hình 2 như sau:

Hình gồm hình chữ nhật BCEG và hình thang ABEG.

Diện tích hình chữ nhật là: EC. BC = 40 . 60 = 2400 ($m^2$)

Vì EG = BC nên EG = 60 m; AG = AB – GB = AB – EC = 120 – 40 = 80 (m)

Diện tích hình thang BCEG là: (60 + 200). 80 : 2 = 10400 ($m^2$)

Vậy diện tích hình 2 là: 2400 + 10400 = 12800 ($m^2$)

Giải bài 12 trang 78 Sách bài tậpToán 6 – Chân trời sáng tạo

Đề bài

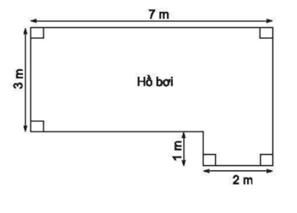
Tính chu vi và diện tích của hồ bơi có kích thước như hình vẽ sau:

Phương pháp giải - Xem chi tiết

Chia hình trên thành 2 hình chữ nhật để tính diện tích. Chu vi ta tính được ngay.

Lời giải chi tiết

Ta chia hình trên thành 2 hình chữ nhật như sau:

Hình gồm hình chữ nhật DGFE ( chiều dài 2m, chiều rộng 1m) và hình chữ nhật ABGC (chiều dài 7m chiều rộng 3m)

Suy ra BG = AC = 3m, FG = ED = 1m, CD = CG – DG = AB – EF = 7 – 2 = 5m

Chu vi của bể bơi là: AC + AB + BF + EF + ED + DC = 3 + 7 + 4 + 2 + 1 + 5 = 22(m)

Diện tích hình chữ nhật ABGC là: 7.3 = 21 ($m^2$)

Diện tích hình chữ nhật DGFE là: 2. 1 = 2($m^2$)

Diện tích bể bơi là: 21 + 2 = 23 ($m^2$)

Giải bài 13 trang 78 Sách bài tậpToán 6 – Chân trời sáng tạo

Đề bài

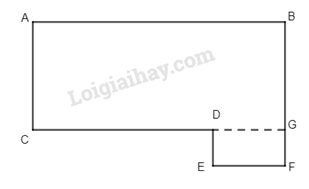
Tính diện tích của hình sau:

Phương pháp giải - Xem chi tiết

Diện tích của hình bằng tổng diện tích hình bình hành và diện tích hình tam giác.

Lời giải chi tiết

Hình trên gồm hình bình hành ( với đáy dài 15 cm, chiều cao 21 cm) và hình tam giác với đáy 20 cm và chiều cao là 21 cm.

Vậy tổng diện tích của hình là: 15.21 + 20.21:2 = 525 ($m^2$)

Giải bài 14 trang 78 Sách bài tậpToán 6 – Chân trời sáng tạo

Đề bài

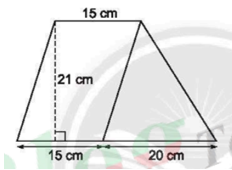
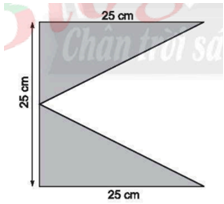
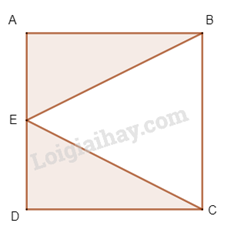
Tính diện tích của hình sau:

Phương pháp giải - Xem chi tiết

Diện tích của hình bằng hiệu diện tích hình vuông lớn và diện tích hình tam giác.

Lời giải chi tiết

Dễ thấy diện tích hình trên bằng hiệu diện tích hình vuông ABCD và diện tích tam giác BEC.

Ta có:

Diện tích hình vuông ABCD là: 25. 25 = 625 ($m^2$)

Diện tích tam giác BEC là: 25 . 25 : 2 = 312,5 ($m^2$)

Vậy diện tích cần tính là: 625 – 312,5 = 312,5 ($m^2$)