Giải bài 1 trang 67 Sách bài tậpToán 6 – Chân trời sáng tạo
Đề bài
Cho hình vuông ABCD có AB = 7cm. Tính độ dài các đoạn thẳng BC, DC, AD.
Phương pháp giải - Xem chi tiết
Dựa vào đặc điểm về cạnh của hình vuông.
Lời giải chi tiết
ABCD là hình vuông nên AB = BC = DC = AD = 7cm.
Đề bài
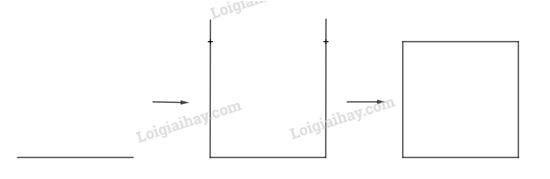
Dùng thước và eke để vẽ hình vuông có độ dài cạnh 5cm
Phương pháp giải - Xem chi tiết
Mô tả các bước vẽ hình vuông bằng thước và êke
Lời giải chi tiết
- Dùng thước vẽ đoạn thẳng AB = 5 cm
- Dùng eke và thước vẽ các đường thẳng vuông góc với AB tại A và B.
- Trên đường vuông góc tại A lấy điểm D với AD = 5cm. Trên đường vuông góc tại B lấy điểm C với BC = 5cm.
- Kẻ đoạn thẳng nối C và D ta được tứ giác ABCD là hình vuông có độ dài cạnh 5cm
Đề bài
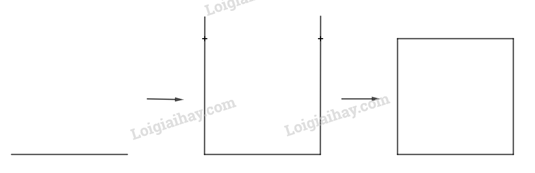
Hãy vẽ một hình vuông có cạnh là 8 cm rồi dùng compa so sánh hai đường chéo của hình vuông đó.
Phương pháp giải - Xem chi tiết
Bước 1: Vẽ hình vuông cạnh 8cm.
Bước 2: Xác định hai đường chéo và so sánh chúng bằng compa.
Lời giải chi tiết
- Dùng thước vẽ đoạn thẳng AB = 8 cm
- Dùng eke và thước vẽ các đường thẳng vuông góc với AB tại A và B.
- Trên đường vuông góc tại A lấy điểm D với AD = 8cm. Trên đường vuông góc tại B lấy điểm C với BC = 8cm.
- Kẻ đoạn thẳng nối C và D ta được tứ giác ABCD là hình vuông có độ dài cạnh 8cm
Nối 2 đường chéo AC và BD. Dùng comp so sánh 2 bán kính lần lượt là AC và BD dễ dàng suy ra hai đường chéo này bằng nhau.
Đề bài
Cho tam giác đều MNP có NP = 3cm. Tính độ dài các cạnh MN, MP
Phương pháp giải - Xem chi tiết
Dựa vào đặc điểm về cạnh của tam giác đều.
Lời giải chi tiết
Tam giác MNP là tam giác đều nên MN = NP = MP = 3cm.
Đề bài
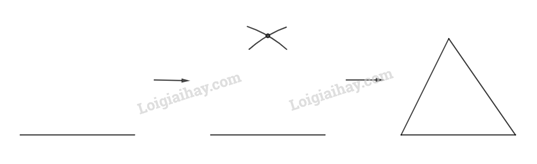
Dùng thước và compa để vẽ tam giác đều có độ dài cạnh 6cm.
Lời giải chi tiết
- Dùng thước vẽ đoạn thẳng AB = 6cm
- Dùng compa vẽ các phần đường tròn cùng bán kính 6cm và có tâm lần lượt là A, B.
- Hai phần đường tròn nói trên cắt nhau tại điểm C.
- Kẻ đoạn thẳng nối C và A, C và B ta có tam giác đều ABC với cạnh 6cm.
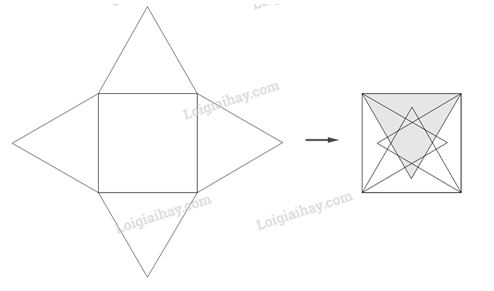
Đề bài
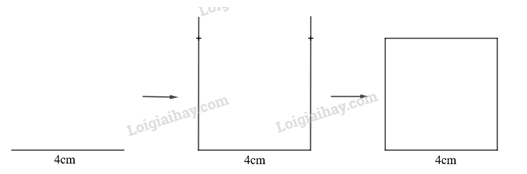
Hãy vẽ một hình vuông có cạnh là 4cm rồi vẽ tiếp ra bên ngoài bốn tam giác đều có cạnh là cạnh hình vuông lên một tờ giấy. Dùng kéo cắt hình vừa vẽ rồi xếp theo các cạnh của hình vuông để có một bao thư.
Lời giải chi tiết
+) Vẽ hình vuông cạnh 4 cm
- Dùng thước vẽ đoạn thẳng AB = 4 cm
- Dùng eke và thước vẽ các đường thẳng vuông góc với AB tại A và B.
- Trên đường vuông góc tại A lấy điểm D với AD = 4 cm. Trên đường vuông góc tại B lấy điểm C với BC = 4 cm.
- Kẻ đoạn thẳng nối C và D ta được tứ giác ABCD là hình vuông có độ dài cạnh 4 cm
+) Vẽ bốn tam giác đều và xếp lại thành bao thư:
Đề bài
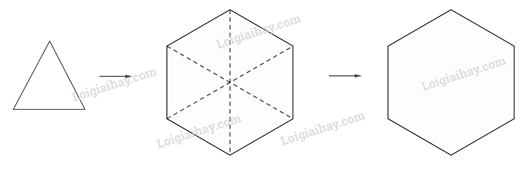
Cho 6 hình tam giác đều (bằng giấy) cùng có độ dài cạnh 5 cm. Hãy nêu cách gấp 6 hình tam giác đó để có một lục giác đều với cạnh bằng 5 cm.
Phương pháp giải - Xem chi tiết
Ghép 6 hình tam giác đều thành 1 hình lục giác đều bằng cách đặt các tam giác sao cho 6 tam giác có chung một đỉnh, các cạnh của chúng hoặc chung 1 đỉnh hoặc chung 1 cạnh.
Lời giải chi tiết
Ta ghép các tam giác sao cho 6 tam có chung 1 đỉnh, các cạnh của chúng hoặc chung 1 đỉnh hoặc chung 1 cạnh, như sau:
Đề bài
Cho lục giác đều MNIJHK với cạnh MN = 6 cm và đường chéo NH = 12 cm. Tính độ dài các đoạn thẳng HK và IK.
Phương pháp giải - Xem chi tiết
Xác định các đoạn HK, IK rồi kết luận độ dài.
Lời giải chi tiết
MNIJHK là lục giác đều nên:
MN = HK = 6 cm (Vì MN và HK đều là cạnh của lục giác đều.)
Vì IK, NH, MJ là các đường chéo chính của lục giác đều nên:
IK = NH = 12 cm
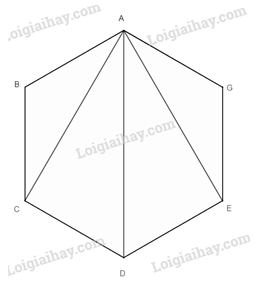
Cho lục giác đều ABCDEG a) Hãy đếm các đường chéo của lục giác vẽ từ mỗi đỉnh của lục giác. Hãy cho biết có bao nhiêu đường chéo được đếm 2 lần. b) Hãy cho biết lục giác trên có bao nhiêu đường chéo.
Cho lục giác đều ABCDEG
a) Hãy đếm các đường chéo của lục giác vẽ từ mỗi đỉnh của lục giác. Hãy cho biết có bao nhiêu đường chéo được đếm 2 lần.
b) Hãy cho biết lục giác trên có bao nhiêu đường chéo.
Câu a
a) Hãy đếm các đường chéo của lục giác vẽ từ mỗi đỉnh của lục giác. Hãy cho biết có bao nhiêu đường chéo được đếm 2 lần.
Phương pháp giải:
a) Bước 1: Vẽ lục giác và các đường chéo từ đỉnh A.
Bước 2: Từ hình vẽ suy ra các đường chéo từ các đỉnh còn lại và đếm số đỉnh được đếm 2 lần.
Lời giải chi tiết:
a) Từ đỉnh A có 3 đường chéo là: AC, AD, AE.
Từ đỉnh B có 3 đường chéo là: BD, BE, BG.
Từ đỉnh C có 3 đường chéo là: CE, CG, CA.
Từ đỉnh D có 3 đường chéo là: DG, DA, DB.
Từ đỉnh E có 3 đường chéo là: EA, EB, EC.
Từ đỉnh G có 3 đường chéo là: GB, GC, GD.
Trong đó 9 đường chéo được đếm 2 lần.
Câu b
b) Hãy cho biết lục giác trên có bao nhiêu đường chéo.
Phương pháp giải:
b) Tính tổng đường chéo. Dựa vào số đường chéo được đếm 2 lần để suy ra số đường chéo của lục giác.
Lời giải chi tiết:
b) Tổng số đường chéo kể cả các đường được đếm 2 lần là:
3 . 6 = 18 (đường)
Mà mỗi đường chéo đều đước đếm 2 lần, do đó số đường chéo của lục giác là:
18 : 2 = 9 (đường chéo)

0 Comments:
Đăng nhận xét