Giải bài tập Toán lớp 8 Bài tập cuối chương 5 trang 28

Bài tập

Giải Toán 8 trang 28 Tập 2

Bài 1 trang 28 Toán 8 Tập 2: Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm M(1; 1), N(4; 1), P(2; −1), Q(−1; −1). Tứ giác MNPQ là hình gì?

A. Hình bình hành;

B. Hình thang cân;

C. Hình vuông;

D. Hình chữ nhật

Lời giải:

Đáp án đúng là: A

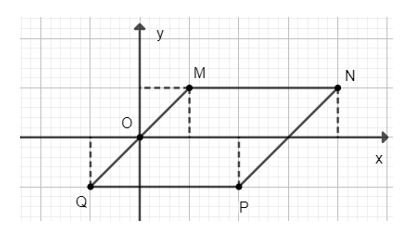
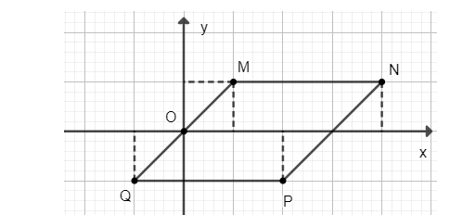
Từ đồ thị hàm số ta thấy tứ giác MNPQ là hình bình hành.

Bài 2 trang 28 Toán 8 Tập 2: Độ dài cạnh MN của tứ giác trong câu 1 là:

A. 3;

B. 5;

C. $\sqrt{3}$;

D. $\sqrt{5}$ .

Lời giải:

Đáp án đúng là: A

Từ đồ thị hàm số ta có MN = 3.

Bài 3 trang 28 Toán 8 Tập 2: Một người bắt đầu mở một vòi nước vào một bể đã chữa sẵn 2 m3 nước, mỗi giờ chảy được 3 m3 nước. Thể tích y(m3) của nước có trong bể sau x giờ bằng:

A. y = 2x + 3;

B. y = 3x + 2;

C. y = 6x;

D. y = x +6.

Lời giải:

Đáp án đúng là: B

Ta có y = 2x + 3.

Bài 4 trang 28 Toán 8 Tập 2: Trong các điểm sau, điểm nào thuộc đồ thị của hàm số y = 2 − 4x?

A. (1; 1);

B. (2; 0);

C. (1; −1);

D. (1; −2).

Lời giải:

Đáp án đúng là: D

Thay D. (1; −2) vào ta có: −2 = 2 – 4 (luôn đúng)

Nên ta có điểm (1; −2) thuộc đồ thị hàm số đã cho.

Bài 5 trang 28 Toán 8 Tập 2: Trong các điểm sau điểm nào thuộc đồ thị cảu hàm số y = −5x + 5?

A.(1; 1);

B. (2; 0);

C. (0; 4);

D. (2; −5).

Lời giải:

Đáp án đúng là: A

Thay vào ta được (1; 1) là điểm thỏa mãn.

Bài 6 trang 28 Toán 8 Tập 2: Đường thẳng song song với đường thẳng y = 2x và cắt trục tung tại điểm có tung độ bằng 1 là:

A. y = 2x – 1;

B. y = −2x – 1;

C. y = 2x +1;

D. y = 6 − 2(1 − x).

Lời giải:

Đáp án đúng là: C

Đường thẳng thỏa mãn yêu cầu bài toán là: y = 2x + 1.

Bài 7 trang 28 Toán 8 Tập 2: Cho hai đường thẳng $y=\frac{1}{2}x+3$  và $y=-\frac{1}{2}x+3$ . Hai đường thẳng đã cho:

A. Cắt nhau tại điểm có hoành độ là 3;

B. Song song với nhau;

C. Cắt nhau tại điểm có tung độ là 3;

D. Trùng nhau.

Lời giải:

Đáp án đúng là: C

Hai đường thẳng trên có hệ số góc khác nhau nên hai đường thẳng này cắt nhau.

Xét phương trình hoành độ giao điểm:

$\frac{1}{2}x+3=-\frac{1}{2}x+3$

⇔ x = 0 suy ra y = 3

Vậy hai đường thẳng cắt nhau tại điểm có tọa độ (0; 3).

Bài 8 trang 28 Toán 8 Tập 2: Cho các hàm số bậc nhất $y=\frac{1}{3}x+2$ ; $y=-\frac{1}{3}x+2$ ; y = −3x + 2. Kết luận nào sau đây là đúng?

A. Đồ thị của các hàm số trên là các đường thẳng song song với nhau;

B. Đồ thị của các hàm số trên là các đường thẳng đi qua gốc tọa độ;

C. Đồ thị của các hàm số trên là các đường thẳng trùng nhau;

D. Đồ thị của các hàm số trên là các đường thẳng cắt nhau tại một điểm.

Lời giải:

Đáp án đúng là: D

Các hàm số bậc nhất $y=\frac{1}{3}x+2$ ; $y=-\frac{1}{3}x+2$ ; y = −3x + 2 có các hệ số góc đôi một khác nhau nên chúng cắt nhau.

Xét phương trình hoành độ giao điểm ta có:

+) $\frac{1}{3}x+2=-\frac{1}{3}x+2\Rightarrow x=0$  ⇒ y = 2.

Vậy giao điểm của $y=\frac{1}{3}x+2$ ; $y=-\frac{1}{3}x+2$  là điểm có tọa độ (0; 2).

+) $\frac{1}{3}x+2=-3x+2$  ⇒ x = 0, y = 2.

Vậy giao điểm của $y=\frac{1}{3}x+2$ ; y = −3x + 2 là điểm có tọa độ (0; 2).

Vậy đồ thị của các hàm số trên là các đường thẳng cắt nhau tại một điểm có tọa độ (0; 2).

Bài 9 trang 28 Toán 8 Tập 2: Đồ thị hàm số $y=\frac{-x+10}{5}$

A. Là một đường thẳng có hệ số góc là −1;

B. Không phải là một đường thẳng;

C. Cắt trục hoành tại điểm có hoành độ 10;

D. Đi qua điểm (200; 50).

Lời giải:

Đáp án đúng là: C

Thay y = 0 ta có $\frac{-x+10}{5}=0\iff x=10$ .

Suy ra đáp án C đúng.

Giải Toán 8 trang 29 Tập 2

Bài 10 trang 29 Toán 8 Tập 2: Cho hàm số $y=f\left(x\right)=\frac{5}{4x}$

a) Tính $a=f\left(\frac{1}{5}\right)$ ; f(−5); $f\left(\frac{4}{5}\right)$ .

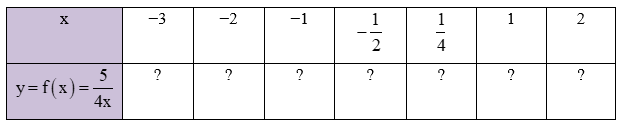
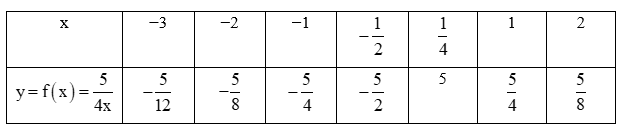
b) Hãy tìm các giá trị tương ứng của các hàm số trong bảng sau:

Lời giải:

a) $f\left(\frac{1}{5}\right)=\frac{5}{4.\frac{1}{5}}=\frac{25}{4}$

$f\left(-5\right)=\frac{5}{4.\left(-5\right)}=-\frac{1}{4}$

$f\left(\frac{4}{5}\right)=\frac{5}{4.\frac{4}{5}}=\frac{25}{10}$

b)

• Với x = −3 ta có: $y=f\left(-3\right)=\frac{5}{4.\left(-3\right)}=-\frac{5}{12}$ ;

• Với x = −2 ta có: $y=f\left(-2\right)=\frac{5}{4.\left(-2\right)}=-\frac{5}{8}$ ;

• Với x = −1 ta có: $y=f\left(-1\right)=\frac{5}{4.\left(-1\right)}=-\frac{5}{4}$ ;

• Với $x=-\frac{1}{2}$ ta có: $y=f\left(-\frac{1}{2}\right)=\frac{5}{4.\left(-\frac{1}{2}\right)}=-\frac{5}{2}$ ;

• Với $x=\frac{1}{4}$  ta có: $y=f\left(\frac{1}{4}\right)=\frac{5}{4.\left(\frac{1}{4}\right)}=5$ ;

• Với x = 1 ta có: $y=f\left(1\right)=\frac{5}{4.1}=\frac{5}{4}$ ;

• Với x = 2 ta có: $y=f\left(2\right)=\frac{5}{4.2}=\frac{5}{8}$ .

Bài 11 trang 29 Toán 8 Tập 2: Cho hàm số y= f(x) = −x2 + 1. Tính f(−3); f(−2); f(−1); f(0); f(1).

Lời giải:

• f(−3) = −(−3)2 + 1= −8

• f(−2) = −(−2)2 + 1 = −3

• f(−1) = −(−1)2 + 1 = 0

• f(0) = −(0)2 + 1 = 1

• f(1) = −(1)2 + 1 = 0

Bài 12 trang 29 Toán 8 Tập 2: Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm A(−2; 0), B(0; 4), C(5; 4), D(3; 0). Tứ giác ABCD là hình gì?

Lời giải:

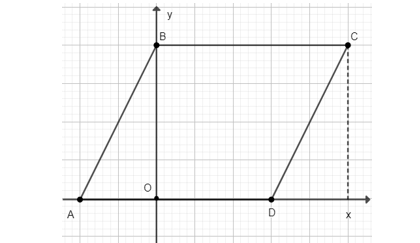
Ta xác định được các điểm A(−2; 0), B(0; 4), C(5; 4), D(3; 0) như sau:

ABCD là hình bình hành.

Bài 13 trang 29 Toán 8 Tập 2: Cho biết đồ thị của hàm số y = ax đi qua điểm $P\left(1;-\frac{4}{5}\right)$

a) Xác định hệ số a.

b) Vẽ điểm trên đồ thị có hoành độ bằng −5.

c) Vẽ điểm trên đồ thị có tung độ bằng 2.

Lời giải:

a) Hàm số y = ax đi qua điểm $P\left(1;-\frac{4}{5}\right)$  suy ra  $a=-\frac{4}{5}$.

Vậy  $y=-\frac{4}{5}x$.
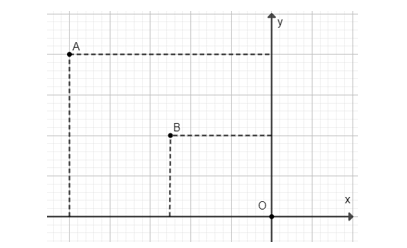
b) Ta có: x = −5 suy ra y = 4, ta xác định được điểm A(−5; 4).

c) Ta có: y = 2 suy ra  $x=-\frac{5}{2}$  ta xác định được điểm $B\left(-\frac{5}{2};2\right)$ .

Bài 14 trang 29 Toán 8 Tập 2: Tìm hàm số có đồ thị là đường thẳng song song với đồ thị hàm số y = −2x + 10.

Lời giải:

Hàm số có đồ thị là đường thẳng song song với đồ thị hàm số y = −2x + 10 là các hàm số có dạng y = ax + b với a = −2 và b ≠ 10.

Bài 15 trang 29 Toán 8 Tập 2: Một người đi bộ với tốc độ không đổi 3 km/ h. Gọi s (km) là quãng đường đi được trong t (giờ).

a) Lập công thức tính s theo t.

b) Vẽ đồ thị của hàm số s theo biến số t.

Lời giải:

a) Công thức: s = 3t

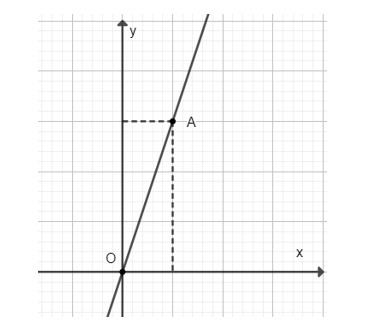
b) Với t = 1 thì s = 3

Đồ thị hàm số s = 3t đi qua O(0; 0) và A(1; 3):

Bài 16 trang 29 Toán 8 Tập 2: Tìm m để các hàm số bậc nhất y = 2mx – 2 và y = 6x + 3 có đồ thị là những đường thẳng song song với nhau.

Lời giải:

y = 2mx – 2 và y = 6x + 3 song song với nhau nên 2m = 6 suy ra m = 3.

Vậy với m = 3 thì thỏa mãn yêu cầu bài toán.

Bài 17 trang 29 Toán 8 Tập 2: Tìm n để các hàm số bậc nhất y = 3nx + 4 và y = 6x + 4 có đồ thị là những đường thẳng trùng nhau.

Lời giải:

y = 3nx + 4 và y = 6x + 4 trùng nhau nên 3n = 6 suy ra n = 2.

Bài 18 trang 29 Toán 8 Tập 2: Tìm k để các hàm số bậc nhất y = kx – 1 và y = 4x + 1 có đồ thị là những đường thẳng cắt nhau.

Lời giải:

y = kx – 1 và y = 4x + 1 có đồ thị là những đường thẳng cắt nhau nên k ≠ 4.

Bài 19 trang 29 Toán 8 Tập 2: Cho hai hàm số y = x + 3, y = −x + 3 có đồ thị lần lượt là các đường thẳng d1 và d2.

a) Bằng cách vẽ hình, tìm tọa độ giao điểm A của hai đường thẳng nói trên và tìm các giao điểm B, C lần lượt của d1 và d2 với trục Ox.

b) Dùng thước đo góc để tìm góc tạo bởi d1 và d2 lần lượt với trục Ox.

c) Tính chu vi và diện tích của tam giác ABC.

Lời giải:

a) Với hàm số y = x + 3 

Cho x = 0 thì y = 3

Cho y = 0 thì x = −3

Đồ thị hàm số y = x + 3 đi qua (0; 3) và B(−3; 0)

Với hàm số y = −x + 3

Cho x = 0 thì y = 3

Cho y = 0 thì x = 3

Đồ thị hàm số y = -x +3 đi qua A(0; 3) và C(3; 0)

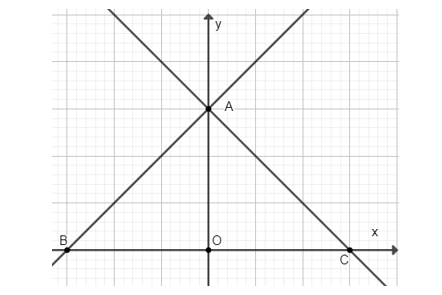
Ta có A (0; 3) là giao điểm của hai đường thẳng nói trên và B(−3; 0), C(3; 0) lần lượt của d1 và d2 với trục Ox.

b) Góc tạo bởi d1 và Ox bằng 45°, góc tạo bởi d2 và Ox bằng 135°.

c)$AC=AB=\sqrt{3^2+3^2}=3\sqrt{2}$

BC = 3 + 3 = 6

Chu vi tam giác ABC là:$3\sqrt{2}+3\sqrt{2}+6=6+6\sqrt{2}$

Diện tích tam giác ABC là: $\frac{1}{2}\mathrm{.3.6}=9$ .