Giải bài tập Toán lớp 8 Bài 5: Hình chữ nhật – Hình vuông

Giải Toán 8 trang 82 Tập 1

Khởi động trang 82 Toán 8 Tập 1: Mỗi viên gạch trong hình bức tường có bề mặt hình chữ nhật được minh hoạ bởi hình bên. Hãy vẽ hình tứ giác ABCD mô phỏng bề mặt một viên gạch vào vở của em.

Lời giải:

Hình b) dưới đây là tứ giác ABCD mô phỏng bề mặt một viên gạch:

1. Hình chữ nhật

Khám phá 1 trang 82 Toán 8 Tập 1: Dùng thước đo góc để đo số đo các góc $\hat{A},\hat{B},\hat{C},\hat{D}$ ở Hình 1 và rút ra nhận xét về số đo của chúng.

Lời giải:

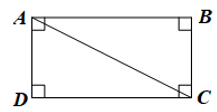
Dùng thước đo góc ta xác định được: $\hat{A}=90°,\hat{B}=90°,\hat{C}=90°,\hat{D}=90°$.

Nhận xét: $\hat{A}=\hat{B}=\hat{C}=\hat{D}\left(=90°\right)$.

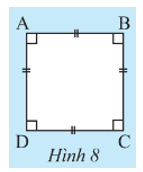
Khám phá 2 trang 82 Toán 8 Tập 1: Cho ABCD là hình chữ nhật.

a) Chứng minh AB // CD và AD // BC.

b) Tam giác ABD và tam giác BAC có bằng nhau không? Vì sao?

Lời giải:

a) Ta có: AB ⊥ AD, CD ⊥ AD nên AB // CD.

               AD ⊥ AB, BC  ⊥ AB nên AD // BC.

b) Tứ giác ABCD có AB // CD và AD // BC nên là hình bình hành.

Do đó AD = BC (tính chất hình bình hành).

Xét DABD và DBAC có:

$\widehat{BAD}=\widehat{ABC}=90°$;

AB là cạnh chung;

AD = BC (chứng minh trên)

Do đó DABD = DBAC (hai cạnh góc vuông).

Giải Toán 8 trang 83 Tập 1

Thực hành 1 trang 83 Toán 8 Tập 1: Cho biết a, b, d lần lượt là độ dài các cạnh và đường chéo của một hình chữ nhật. Thay dấu ? trong bảng sau bằng giá trị thích hợp.

Lời giải:

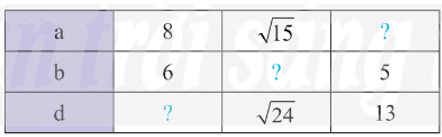
Hình chữ nhật ABCD có $\widehat{ABC}=90°$ và AB, BC hai cạnh, AC là một đường chéo.

Áp dụng định lí Pythagore vào DABC vuông tại B, ta có:

AC2 = AB2 + BC2

Do đó d2 = a2 + b2.

Suy ra $d=\sqrt{a^2+b^2};a=\sqrt{d^2-b^2};b=\sqrt{d^2-a^2}$.

• Với a = 8, b = 6 ta có: $d=\sqrt{a^2+b^2}=\sqrt{8^2+6^2}=10$;

• Với $a=\sqrt{15},d=\sqrt{24}$ ta có:

$b=\sqrt{d^2-a^2}=\sqrt{{\left(\sqrt{24}\right)}^2-{\left(\sqrt{15}\right)}^2}=\sqrt{24-15}=3$;

• Với b = 5, d = 13 ta có:

$a=\sqrt{d^2-b^2}=\sqrt{{13}^2-5^2}=12$.

Vậy ta có bảng sau:

Vận dụng 1 trang 83 Toán 8 Tập 1: Tìm bốn ví dụ về hình chữ nhật trong thực tế.

Lời giải:

Bốn ví dụ về hình chữ nhật trong thực tế: mặt chiếc bàn học; mặt bảng viết; mặt bìa quyển vở; hộp đựng bút.

Khám phá 3 trang 83 Toán 8 Tập 1: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Giải thích các khẳng định sau:

a) Nếu $\widehat{BAD}$ là góc vuông thì $\widehat{ADC}$ và $\widehat{ABC}$ cũng là góc vuông.

b) Nếu AC = BD thì $\widehat{BAD}$ vuông.

Lời giải:

a) Do ABCD là hình bình hành nên AB // CD và AD // BC.

Do $\widehat{BAD}$ là góc vuông nên AD ⊥ AB.

Ta có: AB // CD và AD ⊥ AB nên AD ⊥ CD hay $\widehat{ADC}$ là góc vuông;

           AD // BC và AD ⊥ AB nên BC ⊥ AB hay $\widehat{ABC}$ là góc vuông.

b) Hình bình hành ABCD có AB // CD nên cũng là hình thang có hai cạnh đáy là AB và CD.

Lại có hai đường chéo AC = BD nên là hình thang cân.

Do đó $\widehat{ABC}=\widehat{DCB}$ và $\widehat{BAD}=\widehat{CDA}$.

Tương tự ta cũng có $\widehat{BAD}=\widehat{ABC}$

Suy ra $\widehat{BAD}=\widehat{ABC}=\widehat{DCB}=\widehat{CDA}$

Mà $\widehat{BAD}+\widehat{ABC}+\widehat{DCB}+\widehat{CDA}=360°$

Hay $4\widehat{BAD}=360°$, do đó $\widehat{BAD}=90°$.

Giải Toán 8 trang 84 Tập 1

Thực hành 2 trang 84 Toán 8 Tập 1: Chỉ được sử dụng compa, hãy kiểm tra tứ giác ở Hình 6 có phải là hình chữ nhật hay không.

Lời giải:

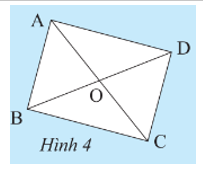
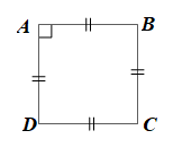
Gọi tứ giác đã cho là ABCD (hình vẽ).

• Dùng compa kiểm tra được AB = CD; AD = BC và AC = BD.

• Tứ giác ABCD có AB = CD và AD = BC nên là hình bình hành.

Lại có hai đường chéo AC = BD nên hình bình hành ABCD là hình chữ nhật.

Vận dụng 2 trang 84 Toán 8 Tập 1: a) Hãy sử dụng êke sao cho chỉ sau ba lần đo ta có thể xác định khung cửa sổ ở Hình 7 có phải là hình chữ nhật hay không.

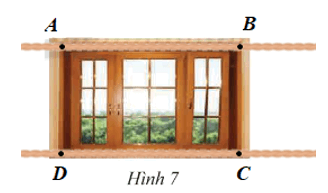
b) Hãy sử dụng một cuộn dây, xác định khung cửa sổ trong Hình 7 có là hình chữ nhật hay không.

Lời giải:

a) Dùng êke ba lần ta đo ba góc $\widehat{DAB},\widehat{ABC},\widehat{BCD}$ thì được $\widehat{DAB}=90°,$$\widehat{ABC}=90°,$$\widehat{BCD}=90°$.

Xét tứ giác ABCD có ba góc vuông nên là hình chữ nhật.

b) Sử dụng một cuộn dây:

• Ta đo đoạn thẳng AB bằng cách đánh dấu 2 điểm trên đoạn dây sao cho hai điểm đánh dấu trùng với hai điểm A, B.

• Đặt điểm đánh dấu thứ nhất trùng với điểm D và kiểm tra thấy điểm đánh dấu còn lại trùng với điểm C. Khi đó AB = CD.

• Làm tương tự ta cũng xác định được AD = BC và AC = BD.

Tứ giác ABCD có AB = CD, AD = BC nên là hình bình hành.

Lại có hai đường chéo AC = BD nên hình bình hành ABCD là hình chữ nhật.

2. Hình vuông

Khám phá 4 trang 84 Toán 8 Tập 1: Cho tứ giác ABCD có bốn góc bằng nhau và có bốn cạnh bằng nhau. Hãy chứng tỏ ABCD vừa là hình thoi vừa là hình chữ nhật.

Lời giải:

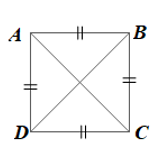
• Tứ giác ABCD có bốn cạnh bằng nhau nên là hình thoi.

• Tứ giác ABCD có bốn góc bằng nhau nên $\widehat{BAD}=\widehat{ABC}=\widehat{DCB}=\widehat{CDA}$.

Mà $\widehat{BAD}+\widehat{ABC}+\widehat{DCB}+\widehat{CDA}=360°$

Hay $4\widehat{BAD}=360°$, suy ra $\widehat{BAD}=90°$.

Do đó $\widehat{BAD}=\widehat{ABC}=\widehat{DCB}=\widehat{CDA}=90°$ nên ABCD là hình chữ nhật.

Vậy ABCD vừa là hình thoi vừa là hình chữ nhật.

Giải Toán 8 trang 85 Tập 1

Khám phá 5 trang 85 Toán 8 Tập 1: Cho hình vuông MNPQ. Chứng minh MNPQ vừa là hình chữ nhật vừa là hình thoi.

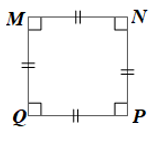
Lời giải:

MNPQ là hình vuông nên là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

Hình vuông MNPQ có bốn góc vuông nên là hình chữ nhật.

Hình vuông MNPQ có bốn cạnh bằng nhau nên là hình thoi.

Vậy hình vuông MNPQ vừa là hình chữ nhật vừa là hình thoi.

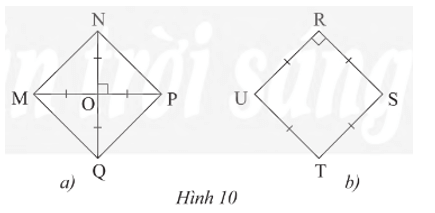
Thực hành 3 trang 85 Toán 8 Tập 1: Tìm hình vuông trong hai hình sau:

Lời giải:

• Hình 10a):

Tứ giác MNPQ có hai đường chéo cắt nhau MP và NQ tại trung điểm O của mỗi đường nên là hình bình hành.

Lại có hai đường chéo MP và NQ vuông góc với nhau tại O nên hình bình hành MNPQ là hình thoi (1)

Mặt khác: MP = OM + OP = 2OM

                 NQ = ON + OQ = 2ON

Mà OM = ON nên MP = NQ.

Ta có MNPQ là hình thoi nên cũng là hình bình hành.

Mà hai đường chéo MP và NQ bằng nhau nên hình bình hành MNPQ là hình chữ nhật (2)

Từ (1) và (2) suy ra MNPQ là hình vuông.

• Hình 10b):

Tứ giác RSTU có RS = ST = TU = UR nên là hình thoi (1)

Do đó RSTU cũng là hình bình hành.

Lại có $\widehat{URS}=90°$ nên hình bình hành RSTU là hình chữ nhật (2)

Từ (1) và (2) suy ra RSTU là hình vuông.

Vận dụng 3 trang 85 Toán 8 Tập 1: Tìm bốn ví dụ về hình vuông trong thực tế.

Lời giải:

Bốn ví dụ về hình vuông trong thực tế: mặt xúc xắc; gạch lát nền hình vuông; mặt bìa hộp bánh pizza hình vuông; mặt kệ gỗ hình vuông.

Khám phá 6 trang 85 Toán 8 Tập 1: Cho hình chữ nhật ABCD. Giải thích tại sao ABCD là hình vuông trong mỗi trường hợp sau:

Trường hợp 1: AB = BC.

Trường hợp 2: AC vuông góc với BD.

Trường hợp 3: AC là đường phân giác của góc BAD.

Lời giải:

• Trường hợp 1: AB = BC.

Do ABCD là hình chữ nhật nên cũng là hình bình hành.

Lại có hai cạnh kề bằng nhau AB = BC nên hình bình hành ABCD là hình thoi.

ABCD vừa là hình chữ nhật vừa là hình thoi nên là hình vuông.

• Trường hợp 2: AC vuông góc với BD.

Do ABCD là hình chữ nhật nên cũng là hình bình hành.

Lại có hai đường chéo vuông góc nên hình bình hành ABCD là hình thoi.

ABCD vừa là hình chữ nhật vừa là hình thoi nên là hình vuông.

• Trường hợp 3: AC là đường phân giác của góc BAD.

Do ABCD là hình chữ nhật nên cũng là hình bình hành.

Lại có đường chéo AC là đường phân giác của góc BAD nên hình bình hành ABCD là hình thoi.

ABCD vừa là hình chữ nhật vừa là hình thoi nên là hình vuông.

Giải Toán 8 trang 86 Tập 1

Khám phá 7 trang 86 Toán 8 Tập 1: Cho hình thoi ABCD. Hãy chứng tỏ:

a) Nếu $\widehat{BAD}$ là góc vuông thì ba góc còn lại của hình thoi cũng là góc vuông.

b) Nếu AC = BD thì $\widehat{BAD}$ là góc vuông.

Lời giải:

a)

Ta có hình thoi ABCD cũng là hình bình hành.

Lại có $\widehat{BAD}=90°$ nên hình bình hành ABCD là hình chữ nhật.

Do đó $\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90°$.

b)

Ta có hình thoi ABCD cũng là hình bình hành.

Lại có hai đường chéo AC = BD nên hình bình hành ABCD là hình chữ nhật.

Do đó $\widehat{BAD}=90°$.

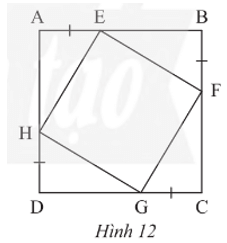
Thực hành 4 trang 86 Toán 8 Tập 1: Trong Hình 12, cho biết ABCD là một hình vuông. Chứng minh rằng:

a) Tứ giác EFGH có ba góc vuông;

b) HE = HG;

c) Tứ giác EFGH là một hình vuông.

Lời giải:

a) Do ABCD là một hình vuông nên $\hat{A}=\hat{B}=\hat{C}=\hat{D}=90°$ và AB = BC = CD = DA.

Mà AE = BF = CG = DH nên EB = FC = GD = HA.

Xét DAEH và DDGH có:

$\hat{A}=\hat{D}=90°$; AE = GH; AH = DG

Do đó DAEH = DDHG (hai cạnh góc vuông)

Suy ra $\widehat{AEH}=\widehat{DHG}$ (hai góc tương ứng).

Xét DAHE có $\widehat{AHE}+\widehat{AEH}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Do đó $\widehat{AHE}+\widehat{DHG}=90°$ hay

$\widehat{EHG}=180°-\left(\widehat{AHE}+\widehat{DHG}\right)=180°-90°=90°$.

Khi đó $\widehat{EHG}$ là một góc vuông.

Chứng minh tương tự ta cũng có $\widehat{HGF},\widehat{GFE}$ là một góc vuông.

Vậy tứ giác EFGH có ba góc vuông.

b) Do DAEH = DDHG (câu a)

Suy ra HE = HG (hai cạnh tương ứng).

c) Chứng minh tương tự câu b, ta cũng có: HE = EF, HE = FG.

Khi đó tứ giác EFGH có HE = HG = EF = FG nên là hình thoi.

Tứ giác EFGH có ba góc vuông nên là hình chữ nhật.

Tứ giác EFGH vừa là hình thoi vừa là hình chữ nhật nên là hình vuông.

Vận dụng 4 trang 86 Toán 8 Tập 1: Bạn Nam kiểm tra mặt kính của chiếc đồng hồ để bàn và nhận thấy có ba góc vuông và hai cạnh kề bằng nhau (Hình 13). Hãy cho biết mặt kính đồng hồ có hình gì?

Lời giải:

Do mặt kính của chiếc đồng hồ để bàn có ba góc vuông vuông mặt kính có hình chữ nhật.

Mà mặt kính có hai cạnh kề bằng nhau nên mặt kính có hình vuông.

Giải Toán 8 trang 87 Tập 1

Bài tập

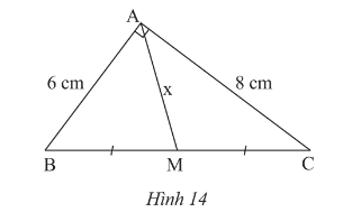
Bài 1 trang 87 Toán 8 Tập 1: Cho Hình 14. Tìm x.

Lời giải:

Áp dụng định lí Pythagore vào DABC vuông tại A, ta có:

BC2 = AB2 + AC2 = 62 + 82 = 100 = 102

Suy ra BC = 10 (cm).

Xét DABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền nên AM bằng nửa cạnh huyền BC.

Do đó $x=AM=\frac{1}{2}BC=\frac{1}{2}.10=5\left(cm\right)$.

Vậy x = 5 cm.

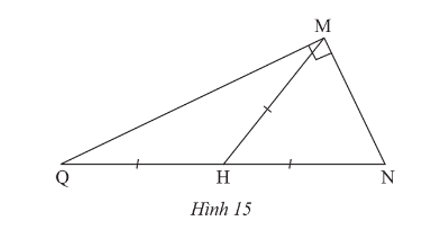
Bài 2 trang 87 Toán 8 Tập 1: Cho Hình 15. Vẽ thêm điểm P để tứ giác MNPQ là hình chữ nhật.

Lời giải:

Lấy điểm P sao cho H là trung điểm của MP (hình vẽ).

Giải thích cách vẽ:

Tứ giác MNPQ có H là trung điểm của hai đường chéo MP và NQ nên là hình bình hành.

Lại có $\widehat{NMQ}=90°$ nên hình bình hành MNPQ là hình chữ nhật.

Bài 3 trang 87 Toán 8 Tập 1: Cho tam giác ABC có đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.

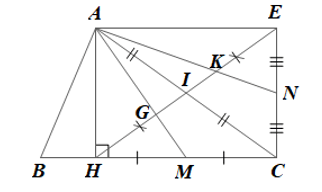
a) Chứng minh tứ giác AHCE là hình chữ nhật.

b) Chứng minh HG = GK = KE.

Lời giải:

a) Do E là điểm đối xứng với H qua I nên I là trung điểm của HE.

Tứ giác AHCE có hai đường chéo AC và HE cắt nhau tại trung điểm I của mỗi đường nên là hình bình hành.

Lại có $\widehat{AHC}=90°$ nên hình bình hành AHCE là hình chữ nhật.

b) Xét DAHC có AM, HI là hai đường trung tuyến cắt nhau tại G nên G là trọng tâm của DAHC.

Suy ra $HG=\frac{2}{3}HI$ và $IG=\frac{1}{2}HG$.

Chứng minh tương tự đối với DAEC có K là trọng tâm của  DAEC.

Suy ra $EK=\frac{2}{3}EI$ và $IK=\frac{1}{2}EK$.

Ta có: $HG=\frac{2}{3}HI$, $EK=\frac{2}{3}EI$ và HI = EI nên $HG=EK\left(=\frac{2}{3}EI\right)$.

Lại có: $IG=\frac{1}{2}HG$ và $IK=\frac{1}{2}EK$ nên $IG=IK=\frac{1}{2}HG$

Mặt khác $GK=IG+IK=\frac{1}{2}HG+\frac{1}{2}HG=HG$.

Vậy HG = GK = KE.

Bài 4 trang 87 Toán 8 Tập 1: Cho tam giác ABC vuông tại A (AB < AC). Gọi D là trung điểm của BC. Vẽ DE // AB, vẽ DF // AC (E ∈ AC, F ∈ AB). Chứng minh rằng:

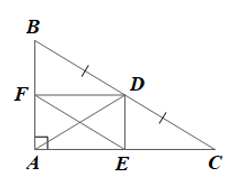
a) Tứ giác AEDF là hình chữ nhật.

b) Tứ giác BFED là hình bình hành.

Lời giải:

a) Tam giác ABC vuông tại A nên $\widehat{BAC}=90°$ hay AB ⊥ AC.

Do DE // AB và AB ⊥ AC nên DE ⊥ AC hay $\widehat{DEA}=90°$.

Do DF // AC và AB ⊥ AC nên DF ⊥ AB hay $\widehat{DFA}=90$

Tứ giác AEDF có $\widehat{BAC}=90°$, $\widehat{DEA}=90°$ và $\widehat{DFA}=90$ nên là hình chữ nhật.

b) Do AEDF là hình chữ nhật nên AF = ED và AD = EF (tính chất hình chữ nhật).

Xét DABC có AD là đường trung tuyến ứng với cạnh huyền BC nên bằng nửa cạnh huyền BC, do đó $AD=DB=DC=\frac{1}{2}BC$.

Từ đó suy ra $AD=EF=DB=DC=\frac{1}{2}BC$

Xét DBDF và DEFD có:

$\widehat{BFD}=\widehat{EDF}=90°$;

BD = EF (chứng minh trên);

DF là cạnh chung.

Do đó DBDF = DEFD (cạnh huyền – cạnh góc vuông).

Suy ra FB = DE (hai cạnh tương ứng).

Xét tứ giác BFED có FB = DE và FB // DE (do AB // DE) nên là hình bình hành.

Bài 5 trang 87 Toán 8 Tập 1: Lấy một tờ giấy, gấp làm tư để có một góc vuông như trong Hình 16, dùng kéo cắt theo đường MN sao cho OM = ON. Mở phần giấy cắt được ra ta được một tứ giác.

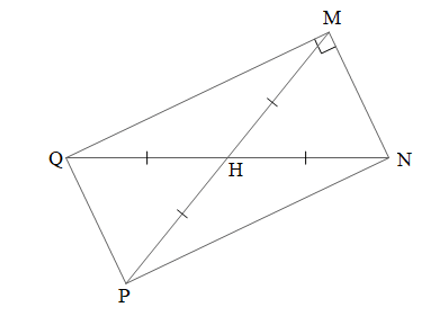
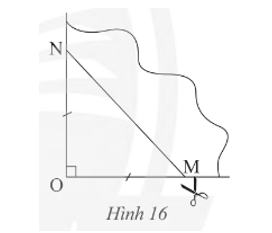
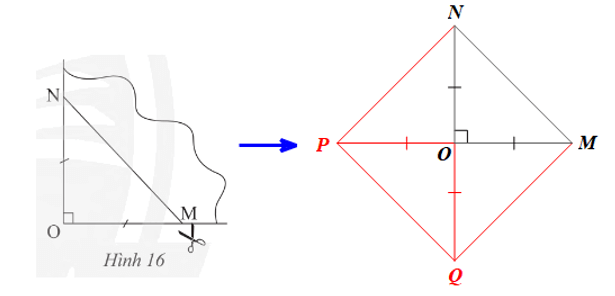
Tứ giác đó là hình gì? Giải thích kết luận của em.

Lời giải:

Mở phần giấy cắt được ra ta được một tứ giác MNPQ như hình vẽ trên.

Ta có OM = ON = OP = OQ nên:

• O là trung điểm của MP và NQ;

• MP = OM + OP = 2OM và NQ = ON + OQ = 2ON

Suy ra MP = NQ.

Xét tứ giác MNPQ có hai đường chéo MP và NQ cắt nhau tại trung điểm O của mỗi đường nên là hình bình hành.

Lại có hai đường chéo bằng nhau MP = NQ nên là hình chữ nhật.

Mặt khác MP ⊥ NQ nên hình chữ nhật MNPQ có hai đường chéo vuông góc với nhau.

Do đó MNPQ là hình vuông.

Video bài giảng Toán 8 Bài 5: Hình chữ nhật – Hình vuông - Chân trời sáng tạo