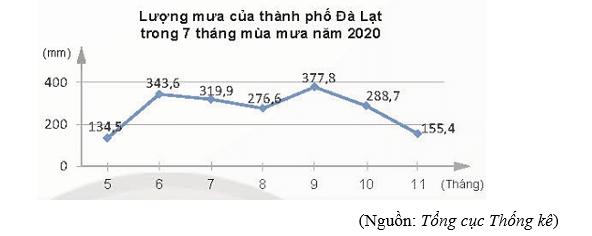
Quan sát biểu đồ và cho biết số lượng mưa ở mỗi tháng là bao nhiêu.
Lời giải:
Lượng mưa tháng 5 là 134,5 mm;
Lượng mưa tháng 6 là 343,6 mm;
Lượng mưa tháng 7 là 319,9 mm;
Lượng mưa tháng 8 là 276,6 mm;
Lượng mưa tháng 9 là 377,8 mm;
Lượng mưa tháng 10 là 288,7 mm;
Lượng mưa tháng 11 là 155,4 mm.
1. Khái niệm hàm số
h (giờ) | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
d (°C) | 36 | 37 | 36 | 37 | 38 | 37 | 38 | 39 | 39 |
Ứng với mỗi giờ em đọc được bao nhiêu số chỉ nhiệt độ?
b) Thời gian t (giờ) để một vật chuyển động đều đi hết quang đường 180 km tỉ lệ nghịch với vận tốc v (km/h) của nó theo công thức: .
Tính và lập bảng các giá trị tương ứng của t khi v lần lượt bằng 10; 20; 30; 60; 180.
Ứng với mỗi giá trị của đại lượng v em tính được bao nhiêu giá trị của đại lượng t?
Lời giải:
a) Ứng với mỗi giờ chỉ đọc được một số chỉ nhiệt độ.
Ứng với 7h thì nhiệt độ là (36°C)
Ứng với 8h thì nhiệt độ là (37°C)
Ứng với 9h thì nhiệt độ là (36°C)
Ứng với 10h thì nhiệt độ là (37°C)
Ứng với 11h thì nhiệt độ là (38°C)
Ứng với 12h thì nhiệt độ là (37°C)
Ứng với 13h thì nhiệt độ là (38°C)
Ứng với 14h thì nhiệt độ là (39°C)
Ứng với 15h thì nhiệt độ là (39°C)
b) Với v = 10
Với v = 20
Với v = 30
Với v = 60
Với v = 180
Ta có bảng:
v | 10 | 20 | 30 | 60 | 180 |
t | 18 | 9 | 6 | 3 | 1 |
Giải Toán 8 trang 7 Tập 2
Thực hành 1 trang 7 Toán 8 Tập 2: Mô tả các đại lượng là hàm số và biến số trong các mô hình sau:
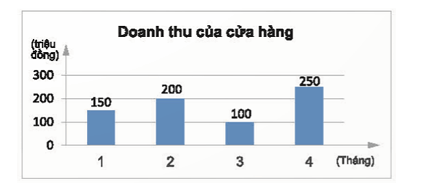
a) Biểu đồ cột chỉ doanh thu y (triệu đồng) của một của hàng trong tháng x.
b) Quãng đường s (km) đi được trong thời gian t (giờ) của một chiếc xe chạy với tốc độ không đổi bằng 40 km/h.
c) Số tiền y (đồng) người mua phải trả cho x quyển vở có giá 10 000 đồng/quyển.
Lời giải:
a) Đại lượng là hàm số là doanh thu y (triệu đồng) của một cửa hàng và biến số là tháng x.
b) Đại lượng là hàm số là quãng đường s (km) đi được và biến số là thời gian t (giờ).
c) Đại lượng là hàm số là số tiền y (đồng) người mua phải trả và biến số là số x quyển vở.
Lời giải:
F là một hàm số theo biến C vì với mỗi giá trị của C chỉ cho ta duy nhất một giá trị của F.
2. Giá trị của hàm số
x | 1 | 2 | 3 | 4 | … |
y = 2x + 3 | 5 | 7 | 9 | … | … |
a) Tính y khi x = 4.
b) Cho x một giá trị tùy ý, tính giá trị tương ứng của y.
Lời giải:
a) Với x = 4 ta có: y = 2.4 + 3 = 11
b) Với x = 10 ta có: y = 10.4 + 3 = 43.
Ta có bảng sau:
x | 1 | 2 | 3 | 4 | 10 |
y = 2x + 3 | 5 | 7 | 9 | 11 | 43 |
Giải Toán 8 trang 8 Tập 2
x | −3 | −2 | −1 | 1 | 2 | 3 |
y | −6 | −4 | −2 | 2 | 4 | 6 |
Đại lượng y có phải là hàm số của đại lượng x không?
b) Cho hàm số y = f(x) = x2.
- Tính f(2); f(−3).
- Lập bảng giá trị của hàm số với x lần lượt bằng −3; −2; −1; 0; 1; 2; 3.
Lời giải:
a) Với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.
b) f(2) = 22 = 4; f(−3) = (−3)2 = 9.
Ta có f(0) = 02 = 0; f(−1) = (−1)2 = 1;
f(2) = 22 = 4; f(3) = 32 = 9.
Từ đó ta có bảng:
x | −3 | −2 | −1 | 0 | 1 | 2 | 3 |
y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Lời giải:
Ta có: C = d trong đó, C là chu vi đường tròn; d là đường kính và là số pi.
Do đó, f(d) = .d
Với d = 1 ⇒ f(1) = .1 =
d = 2 ⇒ f(2) = .2 = 2
d = 3 ⇒ f(3) = .3 = 3
d = 4 ⇒ f(4) = .4 = 4
Ta thu được bảng sau:
d | 1 | 2 | 3 | 4 |
f(d) | 2 | 3 | 4 |
Bài tập
Giải Toán 8 trang 9 Tập 2
Giải thích.
a)
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
b)
Lời giải:
a) Dựa vào bảng, ta thấy với một giá trị của x ta chỉ nhận được một giá trị của y tương ứng, do đó đại lượng y là hàm số của đại lượng x.
b) Dựa vào bảng, ta thấy tồn tại một giá trị của x ta có thể nhận được hai giá trị của y tương ứng, do đó đại lượng y không là hàm số của đại lượng x.
Ví dụ: Khi x = 2 thì y = hoặc y = .
Bài 2 trang 9 Toán 8 Tập 2: Cho hàm số y = f(x) = 3x.
a) Tính f(1); f(−2); .
b) Lập bảng các giá trị tương ứng của y khi x lần lượt nhận các giá trị: −3; −2; −1; 0; 1; 2; 3.
Lời giải:
a) Ta có:
• f(1) = 3.1 = 3;
• f(−2) = 3.(−2) = −6;
• .
b) Ta có f(−3) = 3.(−3) = −9; f(−1) = 3.(−1) = −3;
f(0) = 3.0 = 0; f(2) = 3.2 = 6; f(3) = 3.3 = 9.
Từ đó ta có bảng sau:
x | −3 | −2 | −1 | 0 | 1 | 2 | 3 |
y = 3x | −9 | −6 | −3 | 0 | 3 | 6 | 9 |
Bài 3 trang 9 Toán 8 Tập 2: Cho hàm số y = f(x) = x2 + 4. Tính f(−3); f(−2); f(−1); f(0); f(1).
Lời giải:
• f(−3) = (−3)2 + 4 = 9 + 4 = 13;+
• f(−2) = (−2)2 + 4 = 4 + 4 = 8;
• f(−1) = (−1)2 + 4 = 5;
• f(0) = 0 + 4 = 4;
• f(1) = 1 + 4 = 5.
Vậy f(−3) = 13; f(−2) = 8; f(−1) = 5; f(0) = 4; f(1) = 5.
Lời giải:
Đại lượng m là hàm số của đại lượng V vì với mỗi một giá trị của V ta luôn chỉ xác định được một giá trị của m.
Ta có: m = 7,8V
m(10) = 7,8.10 = 78;
m(20) = 7,8.20 = 156;
m(40) = 7,8.40 = 312;
m(50) = 7,8.50 = 390.
Lời giải:
• Với v = 10 ta có ;
• Với v = 20 ta có ;
• Với v = 40 ta có ;
• Với v = 80 ta có .
Khi đó, ta có bảng sau:
v (km/h) | 10 | 20 | 40 | 80 |
t (giờ) | 2 | 1 | 0,5 | 0,25 |


0 Comments:
Đăng nhận xét