Công thức Toán 7 HK1

 

1. Cộng, trừ, nhân, chia số hữu tỉ

a) Cộng và trừ hai số hữu tỉ

Trường hợp 1: Hai phân số cùng mẫu số

Viết hai số hữu tỉ x, y dưới dạng $x=\frac{a}{m};y=\frac{b}{m}$  (a, b, m, n ∈ ℤ, m ≠ 0)

Khi đó ta có:

$x+y=\frac{a}{m}+\frac{b}{m}=\frac{a+b}{m}$;

$x-y=\frac{a}{m}-\frac{b}{m}=\frac{a-b}{m}$.

Trường hợp 2: Hai phân số khác mẫu số

Viết hai số hữu tỉ x, y dưới dạng $x=\frac{a}{m};y=\frac{b}{n}$ (a, b, m, n ∈ℤ, m, n ≠ 0)

Khi đó ta có:

$x+y=\frac{a}{m}+\frac{b}{n}=\frac{a.n}{m.n}+\frac{b.m}{n.m}=\frac{a.n+b.m}{m.n}$;

$x-y=\frac{a}{m}-\frac{b}{n}=\frac{a.n}{m.n}-\frac{b.m}{n.m}=\frac{a.n-b.m}{m.n}$.

Tính chất: Phép cộng số hữu tỉ cũng có các tính chất của phép cộng phân số:

- Tính chất giao hoán: x + y = y + x

- Tính chất kết hợp: (x + y) + z = x + (y + z)

- Tính chất cộng với 0:x + 0 = x

b) Nhân hai số hữu tỉ

Với hai số hữu tỉ $x=\frac{a}{b};y=\frac{c}{d}$ (b, d ≠ 0) ta có:

$x.y=\frac{a}{b}.\frac{c}{d}=\frac{ac}{bd}$.

Tính chất: Phép nhân trong ℚ có các tính chất cơ bản sau:

- Tính chất giao hoán: a. b = b. a

- Tính chất kết hợp: (a. b). c = a. (b. c)

- Nhân với 1: a. 1 = a

- Tính chất phân phối của phép nhân đối với phép cộng: a. (b + c) = a. b + a. c

c) Chia hai số hữu tỉ

Với hai số hữu tỉ $x=\frac{a}{b};y=\frac{c}{d}$ (b, d, y ≠ 0) ta có:

$x:y=\frac{a}{b}:\frac{c}{d}=\frac{a}{b}.\frac{d}{c}=\frac{a.d}{b.c}$.

2. Lũy thừa với số mũ tự nhiên

a) Lũy thừa với số mũ tự nhiên

Quy ước:

$x^0=1$ (x ∈ ℚ, x ≠ 0);

$x^1=x$ (x ∈ ℚ).

b) Nhân hai lũy thừa cùng cơ số

xm .xn = xm+n (x $\in$ ℚ, m, n $\in$ ℕ);

c) Chia hai lũy thừa cùng cơ số

xm : xn = xm-n (x ≠ 0, m ≥ n);

d) Lũy thừa của lũy thừa

 = xm.n (x $\in$ ℚ, m, n $\in$ ℕ).

3. Thứ tự thực hiện phép tính, quy tắc chuyển vế

1. Thứ tự thực hiện phép tính

Thứ tự thực hiện phép tính đối với các số tự nhiên vẫn đúng với các số hữu tỉ:

- Với các biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia, ta thực hiện các phép tính từ trái sang phải.

- Với các biểu thức không có dấu ngoặc, ta thực hiện theo thứ tự:

Lũy thừa → Nhân và chia → Cộng và trừ.

- Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau 

Thứ tự thực hiện các dấu ngoặc: ngoặc tròn → ngoặc vuông → ngoặc nhọn

2. Quy tắc chuyển vế

Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “” và dấu “”  đổi thành dấu “+”.

Nếu A + B = C thì A = C – B;

Nếu A – B = C thì A = C + B.

Tính chất của đẳng thức:

Nếu A = B thì B = A; A + C = B + C.

4. Tìm căn bậc hai số học của một số không âm


Căn bậc hai số học của số a không âm là số x không âm sao cho x2 = a.

Kí hiệu là $\sqrt{a}$

Cho a ≥ 0. Khi đó:

+) $\sqrt{a}=x\iff \left(\begin{array}{c}x\ge 0\\ x^2=a\end{array}\right)$;

+) ${\left(\sqrt{a}\right)}^2=a$.

5. Tính chất phép cộng, phép trừ các số thực

Trong tập hợp các số thực, các phép tính có các tính chất đối với phép cộng, phép trừ như sau:

Với a, b, c là các số thực ta có:

• Tính chất giao hoán: a + b = b + a;

• Tính chất kết hợp: (a + b) + c = a + (b + c);

• Tính chất cộng với số 0: a + 0 = 0 + a = a;

• Tính chất cộng với số đối: a + (‒a) = (‒a) + a = 0.

- Ta có thể chuyển phép trừ cho một số thực thành phép cộng với số đối của số thực đó:

a – b = a + (‒b)

- Ta cũng có quy tắc chuyển vế và quy tắc bỏ dấu ngoặc đối với phép tính của các số thực:

• Quy tắc chuyển vế:

a + b = c thì a = c – b;

a – b = c thì a = c + b.

• Quy tắc bỏ dấu ngoặc:

a + (b – c) = a + b – c;

a – (b – c + d) = a – b + c – d.

6. Tính chất của phép nhân các số thực

Trong tập hợp các số thực, các phép tính có các tính chất đối với phép nhân như sau:

Với a, b, c là các số thực ta có:

• Tính chất giao hoán: a. b = b. a;

• Tính chất kết hợp: (a. b). c = a. (b. c);

• Tính chất nhân với số 1: a. 1 = 1. a = a;

• Tính chất phân phối của phép nhân đối với phép cộng: a. (b + c) = a. b + a. c;

• Với mỗi số thực a ≠ 0, có số nghịch đảo $\frac{1}{a}$sao cho $a.\frac{1}{a}=1$.

Ta có thể chuyển phép chia cho một số thực khác 0 về phép nhân với số nghịch đảo của số thực đó:

a : b = $a.\frac{1}{b}$(với b ≠ 0)

7. Luỹ thừa của số thực với số mũ tự nhiên

Trong tập hợp các số thực, các phép tính luỹ thừa với số mũ tự nhiên như sau:

Với x, y là các số thực và m, n là các số tự nhiên:

• Luỹ thừa với số mũ tự nhiên: $x^n=\underset{n\text{thua so x}}{\underset{}{x.x.\mathrm{...}.x}};$

• Tích và thương của hai luỹ thừa cùng cơ số: với x ≠ 0, m ≥ n ta có

xm. xn = xm + n;

xm : xn = xm – n

• Luỹ thừa của một luỹ thừa: (xm)n = xm. n

• Luỹ thừa của một tích, một thương:

(x. y)n = xn. yn;

${\left(\frac{\text{x}}{\text{y}}\right)}^{\text{n}}=\frac{{\text{x}}^{\text{n}}}{{\text{y}}^{\text{n}}}$ (với y ≠ 0)

• Quy ước: x0 = 1 và x1 = x.

8.Tính giá trị tuyệt đối của một số thực

Khái niệm: Khoảng cách từ điểm x đến điểm gốc O trên trục số được gọi là giá trị tuyệt đối của số x, kí hiệu là |x|.

• Với mọi số thực x thì |x| ≥ 0;

• Với mọi số thực x thì |‒x| = |x|;

Tính chất:

• Nếu x > 0 thì |x| = x.

• Nếu x = 0 thì |x| = 0.

• Nếu x < 0 thì |x| = ‒x.

Ta cũng có thể viết như sau:

$\left(x\right)=\left(\begin{array}{c}x\text{khi}x>0\\ 0\text{khi}x=0\\ -x\text{khi}x<0\end{array}\right)$

+ Với số thực không âm a ≥ 0, ta có: |x| = a thì x = a hoặc x = −a;

+ Với mọi số thực x, y ta có: |x| = |y| thì x = a hoặc x = −y.

9.Tính diện tích, thể tích hình hộp chữ nhật, hình lập phương

Ta kí hiệu Sxq là diện tích xung quanh, V là thể tích.

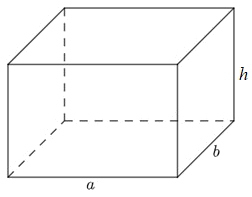
a) Hình hộp chữ nhật

Hình hộp chữ nhật có các kích thước:

+ Chiều dài đáy là a;

+ Chiều rộng đáy là b;

+ Chiều cao của hình hộp chữ nhật là h.

Diện tích xung quanh hình hộp chữ nhật: Sxq = 2. (a + b). h

Diện tích đáy hình hộp chữ nhật: Sđáy = a.b

Thể tích hình hộp chữ nhật: V = a. b. h = S. h (trong đó S là diện tích đáy)

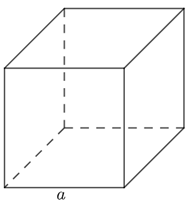
b) Hình lập phương

Hình lập phương có cạnh là a.

Diện tích xung quanh hình lập phương: Sxq = 4. a2.

Thể tích hình lập phương: V = a3.

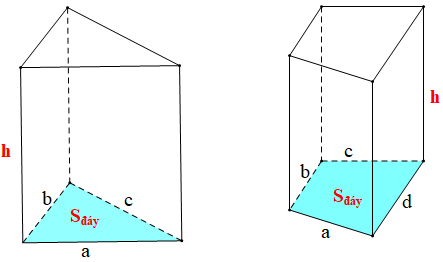
10.Tính diện tích và thể tích của hình lăng trụ đứng

+ Diện tích xung quanh của hình lăng trụ đứng:

Sxq = Cđáy. h (trong đó Cđáy là chu vi đáy, h là chiều cao)

Trong đó:

• Chu vi của đáy là tam giác: Cđáy = a + b + c (với a, b, c là độ dài ba cạnh của tam giác)

• Chu vi của đáy là tứ giác: Cđáy = a + b + c + d (với a, b, c, d là độ dài bốn cạnh của tứ giác)

+ Thể tích của hình lăng trụ đứng:

V = Sđáy. h (trong đó Sđáy là diện tích đáy, h là chiều cao)

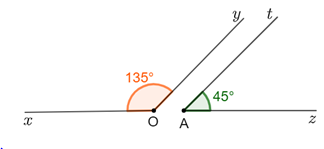
11. Hai góc kề nhau, bù nhau và kề bù

a) Hai góc kề nhau

Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm khác phía đối với đường thẳng chứa cạnh chung đó.

 kề nhau thì tia Oy là tia nằm giữa hai tia Ox và Oz, khi đó:

 kề nhau thì 

b) Hai góc bù nhau

Hai góc bù nhau là hai góc có tổng số đo bằng 180°.

c) Hai góc kề bù

Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.

Hai góc kề bù còn được hiểu là hai góc vừa kề nhau, vừa bù nhau.

kề bù thì tia Oy nằm giữa hai tia Ox, Oz và 

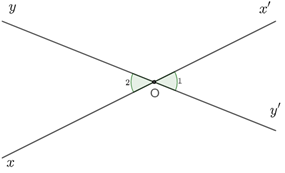
13. Tính chất hai góc đối đỉnh

- Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

- Hai góc đối đỉnh thì bằng nhau.

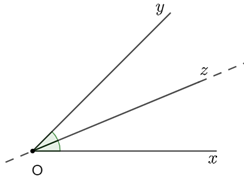
14. Tính chất tia phân giác của một góc

Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.

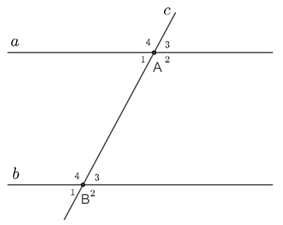
15. Tính chất hai đường thẳng song song

 - Cho ba đường thẳng a, b, c phân biệt tạo thành các góc như hình vẽ.

+) Nếu a // b thì A1^=B1^, A2^=B2^, A3^=B3^, A4^=B4^(các cặp góc đồng vị bằng nhau)

Ngược lại, nếu A1^=B1^(hoặc A2^=B2^, hoặc A3^=B3^, hoặc A4^=B4^) (hai góc đồng vị bằng nhau) thì a // b.

+) Nếu a // b thì A1^=B3^, A2^=B4^(các cặp góc so le trong bằng nhau)

Ngược lại, nếu A1^=B3^(hoặc A2^=B4^) (hai góc so le trong bằng nhau) thì a // b.

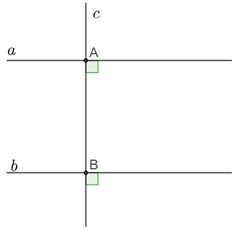
c⊥a;c⊥b suy ra a // b.