1. Tam giác là gì? Các trường hợp đặc biệt của tam giác?
Để giải các bài tập công thức tính diện tích tam giác, đầu tiên bạn bạn cần xác định loại tam giác đó là gì, từ đó tìm ra công thức tính diện tích chính xác nhất. Hiện tại, các loại tam giác phổ biến được chia thành 7 dạng chính như sau:
- Tam giác thường: Tam giác là đa giác lồi có 3 cạnh với 3 đỉnh nối 3 cạnh bên không thẳng hàng. Tổng các góc trong tam giác bằng 180°
- Tam giác vuông: là tam giác có 1 góc bằng 90°
- Tam giác cân: là tam giác có hai cạnh bên bằng nhau, 2 góc kề cạnh đáy bằng nhau.
- Tam giác đều: là tam giác có 3 cạnh bên bằng nhau, 3 góc bằng nhau và bằng 60°
- Tam giác vuông cân: là tam giác có 1 góc bằng 90°, 2 cạnh bên bằng nhau, 2 góc đáy bằng 45°.
- Tam giác tù: là tam giác có 1 góc lớn hơn 90°
- Tam giác nhọn: là tam giác có ba góc trong tam giác nhỏ hơn 90°
Các bạn có thể xem thêm trên Wikipedia bài viết về tam giác để tìm hiểu chi tiết về hình này.
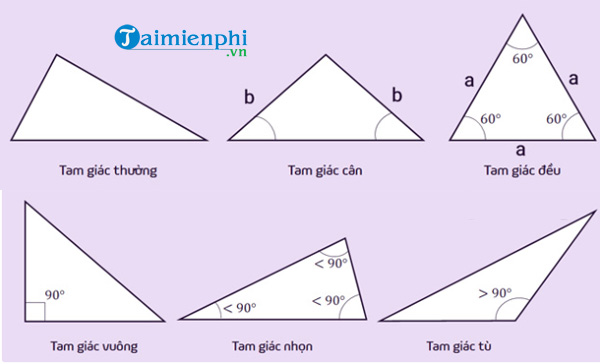
Hình ảnh các loại tam giác phổ biến
- Xem thêm: Cách tính đường cao trong tam giác
2. Cách tính diện tích tam giác
Để dễ hình dung hơn, Taimienphi.vn sẽ hướng dẫn các bạn cách tính diện tích hình tam giác theo thứ tự từ tam giác thường đến các trường hợp đặc biệt của tam giác như tam giác vuông, cân, đều,...
* Cách tính diện tích tam giác thường
- Diễn giải: Diện tích tam giác thường được tính bằng cách nhân chiều cao với độ dài đáy, sau đó tất cả chia cho 2. Nói cách khác, diện tích tam giác thường sẽ bằng 1/2 tích của chiều cao và chiều dài cạnh đáy của tam giác.
- Công thức tính diện tích tam giác thường
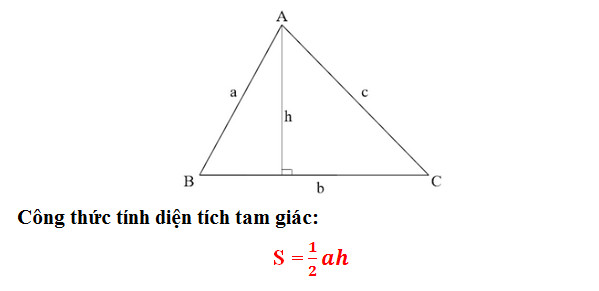
Trong đó:
+ a: Chiều dài đáy tam giác (đáy là một trong 3 cạnh của tam giác tùy theo quy đặt của người tính)
+ h: Chiều cao của tam giác, ứng với phần đáy chiếu lên (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy, đồng thời vuông góc với đáy của một tam giác).
- Nếu đã có diện tích tam giác, bạn có thể tìm đường cao hoặc cạnh tam giác với công thức như sau:
+ Đường cao H= (Sx2)/ a
+ Công thức tính cạnh tam giác tương ứng với chiều cao: a= (Sx2)/ h
- Ví dụ: Cho một hình tam giác ABC, trong đó có chiều cao nối từ đỉnh Ảnh xuống đáy BC bằng 3, chiều dài đáy BC bằng 6. Tính diện tích tam giác thường ABC? (Đơn vị tính: cm)

Đáp án: Gọi a =6 và h=3.
Suy ra S = (a x h)/ 2 = (6x3)/2 hoặc 1/2 x (6x3) = 9 cm
* Chú ý: Trường hợp không cho cạnh đáy hoặc chiều cao, mà cho trước diện tích và cạnh còn lại, các bạn hãy áp dụng công thức suy ra ở trên để tính toán.
* Cách tính diện tích tam giác vuông
- Diễn giải: Cách tính diện tích tam giác vuông tương tự với cách tính diện tích tam giác thường, đó là bằng 1/2 tích của chiều cao với chiều dài đáy. Mặc dù vậy hình tam giác vuông sẽ khác biệt hơn so với tam giác thường do thể hiện rõ chiều cao và chiều dài cạnh đáy, và bạn không cần vẽ thêm để tính chiều cao tam giác.
- Công thức tính diện tích tam giác vuông: S = (a x h)/ 2
+ a: Chiều dài đáy tam giác vuông (đáy là một trong 3 cạnh của tam giác và vuông góc với một cạnh còn lại)
+ h: Chiều cao của tam giác, ứng với phần đáy chiếu lên (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy, đồng thời vuông góc với đáy của một tam giác).
Từ đó, suy ra công thức chiều cao, cạnh tương ứng là: h=(Sx2)/ a hoặc a= (Sx2)/ h
- Ví dụ: Có một hình tam giác vuông ABC, vuông góc nhau tại điểm B, chiều dài cạnh đáy BC là 5 cm, chiều cao là 2 cm. Hỏi diện tích của hình tam giác vuông ABC bằng bao nhiêu? Đơn vị tính: cm.
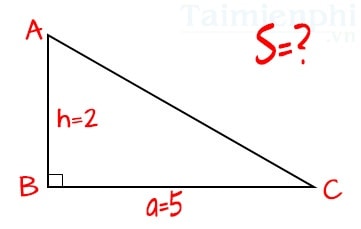
Đáp án: Gọi a =5 và h=2.
Suy ra S = (a x h)/ 2 = (5x2)/2 hoặc 1/2 x (5x2) = 5 cm
Tương tự nếu dữ liệu hỏi ngược về cách tính chiều dài cạnh đáy hoặc chiều cao, các bạn có thể sử dụng công thức suy ra ở trên.
* Cách tính diện tích tam giác cân
Tam giác cân là tam giác trong đó có hai cạnh bên và hai góc bằng nhau. Trong đó cách tính diện tích tam giác cân cũng tương tự cách tính tam giác thường, chỉ cần bạn biết chiều cao tam giác và cạnh đáy.
- Diễn giải: Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.
- Công thức tính diện tích tam giác cân: S = (a x h)/ 2
+ a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
- Ví dụ: Cho một tam giác cân ABC có chiều cao nối từ đỉnh A xuống đáy BC bằng 7 cm, chiều dài đáy cho là 6 cm. Hỏi diện tích của tam giác cân ABC bằng bao nhiêu.
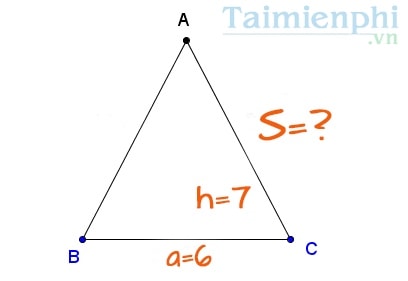
Đáp án: Gọi a =6 và h=7.
Suy ra S = (a x h)/ 2 = (6x7)/2 hoặc 1/2 x (6x7) = 21 cm
* Công thức tính diện tích tam giác vuông cân
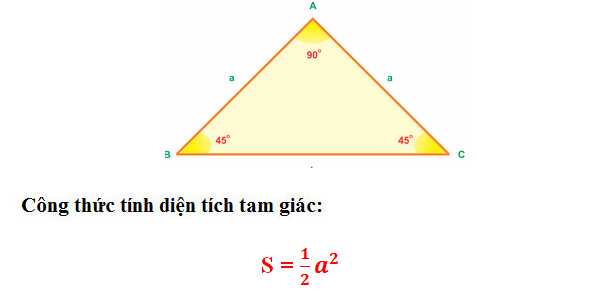
Ví dụ: Cho tam giác ABC vuông cân tại A, có AB = AC = 6cm. Tính diện tích tam giác ABC.
Giải: Do cạnh AB = AC = a = 6cm
Xét tam giác ABC vuông cân tại A, ta có:
S = (a2) : 2 = 36 : 2 = 13 cm2
* Công thức tính diện tích tam giác đều
Tam giác đều là tam giác có 3 cạnh bằng nhau và mỗi góc trong tam giác đều có góc bằng 60 độ, và bất cứ tam giác nào có ba góc bằng nhau cũng được coi là một tam giác đều.
- Công thức diện tích tam giác đều: S = a2 X (√3)/4
Trong đó:
+ a: chiều dài một cạnh bất kỳ trong tam giác đều.
- Ví dụ: Có một tam giác đều ABC với chiều dài các cạnh bằng nhau là 9 cm, biết các góc của tam giác này đều bằng 60 độ. Hỏi diện tích tam giác đều ABC bằng bao nhiêu?
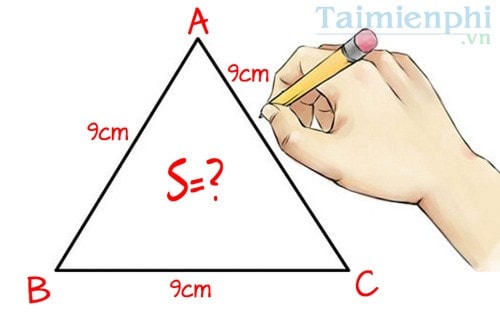
Đáp án: Do mỗi cạnh AB = AC = BC = 9 nên ta có chiều dài cạnh a = 9.
Thay vào công thức diện tích tam giác đều ta có: S = a2 x (√3)/4 = S = 92 x (√3)/4 = 81 x (√3)/4 = 81 x (1,732/4) = 35,07 cm2
3. Các cách tính diện tích tam giác nâng cao
Ngoài những cách tính diện tích tam giác ở trên, thực tế, toán học còn phổ biến các cách tính diện tích tam giác bằng công thức Heron, tính diện tích tam giác bằng góc và hàm lượng giác. Cụ thể:
* Công thức diện tích tam giác khi biết 1 góc
Diện tích tam giác theo Sin là:
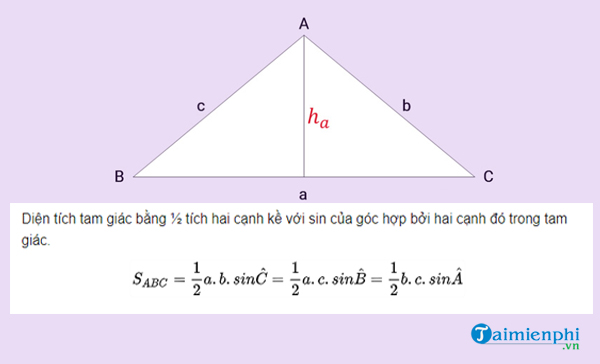
* Công thức tính diện tích tam giác theo công thức Heron
Diện tích tam giác khi biết 3 cạnh:
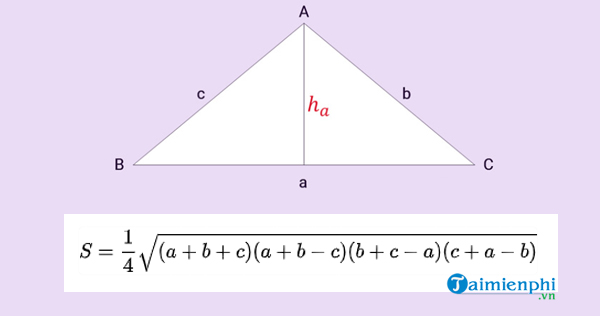
* Cách tính diện tích tam giác mở rộng
Lưu ý: Khi dùng công thức này thì bạn cần chứng minh trước.
Công thức 1:
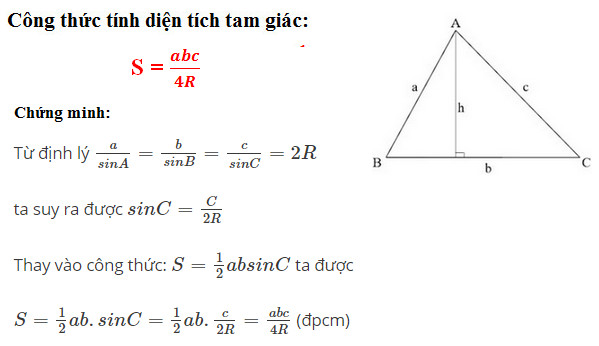
Trong đó:
- a, b, c: Độ dài cạnh của tam giác
- R: Bán kính đường tròn ngoại tiếp tam giác
Công thức 2:
Diện tích tam giác công thức cũng có thể áp dụng:
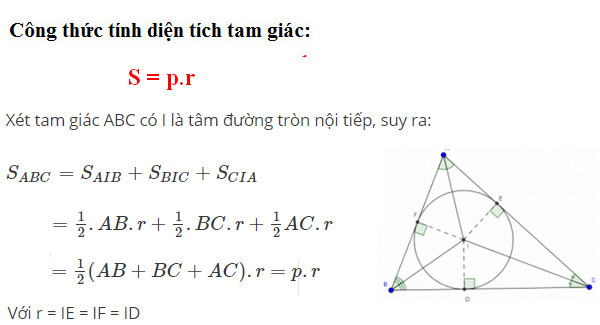
Trong đó:
- p: nửa chu vi tam giác
- r: bán kính đường tròn nội tiếp tam giác
Tùy vào từng công thức mà áp dụng cho các khối lớp khác nhau. Thông thường, diện tích tam giác lớp 5, lớp 8 có công thức cơ bản đơn giản. Từ lớp 10 trở đi thì bạn có thể á dụng các công thức suy rộng nếu đã học kiến thức lượng giác, đường tròn nội, ngoại tiếp.
4. Lưu ý khi làm bài tính diện tích tam giác
- Khi làm, cần chú ý các đơn vị đo lường cần phải giống nhau.
- Với diện tích, đơn vị đo lường tính theo mũ 2, chẳng hạn như m2, cm2 ...
Dù sử dụng công thức tính diện tích tam giác nào đi chăng nữa thì các bạn, các em học sinh, sinh viên cần hiểu rằng, không phải lúc chiều cao cũng nằm trong tam giác, lúc này cần vẽ thêm một chiều cao và cạnh đáy bổ sung. Và quan trọng khi tính diện tích tam giác, cần chú ý chiều cao phải ứng với cạnh đáy nơi nó chiếu xuống.
5. Bài tập tính diện tích tam giác
Ví dụ 1: Một hình tam giác có đáy 15 cm và chiều cao 2,4cm. Tính diện tích hình tam giác đó?
Hướng dẫn giải:
Diện tích hình tam giác là:
15 x 2,4 : 2 = 18 (cm2)
Đáp số: 18cm2
=> Các em có thể tham khảo thêm các bài toán về hình tam giác lớp 5 cơ bản và nâng cao để hiểu hơn về cách giải, làm bài toán này dễ dàng/
-------------------HẾT-------------------
Hiện nay, đã có rất nhiều công cụ hỗ trợ người dùng, đặc biệt là các em học sinh trong việc tính toán, một số phần mềm trên máy tính hỗ trợ tính toán khá phổ biến như FxCalc, DubCen, SpeQ Mathematics, Calculatormatik, Magiccalc, download CocCoc giải toán,…trong đó nhiều người thường tính toán bằng Fxcalc Chức năng CocCoc giải toán khá tiện dụng và hiệu quả. Tất nhiên những phần mềm như vậy chỉ hỗ trợ phần nào, quan trọng nhất vẫn là kiến thức và cách tính được các bạn, các em ghi nhớ và áp dụng đúng.
Các em đã được tìm hiểu về tam giác và cách vẽ tam giác, vậy công thức tính chu vi tam giác là gì, hãy cùng tìm hiểu nhé!
https://thuthuat.taimienphi.vn/cong-thuc-tinh-dien-tich-tam-giac-21883n.aspx
Tác giả: Phạm Nhất Vương

0 Comments:
Đăng nhận xét