Bài tập tính diện tích hình thoi lớp 8

 BÀI TẬP TÍNH DIỆN TÍCH HÌNH THOI LỚP 8 TRONG SGK

Bài 33 (trang 128 SGK Toán 8 Tập 1): Vẽ hình chữ nhật có một cạnh bằng đường chéo của một hình thoi cho trước và có diện tích bằng diện tích của hình thoi đó. Từ đó suy ra cách tính diện tích hình thoi.

Giải:

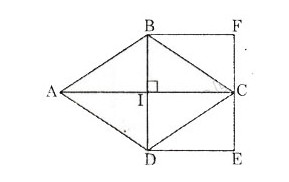
Cho hình thoi ABCD, vẽ hình chữ nhật có một cạnh là đường chéo BD, cạnh kia bằng IC (bằng nửa AC).

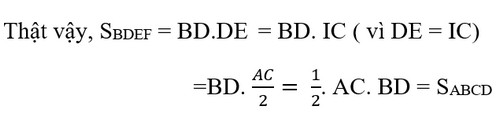
Khi đó diện tích của hình chữ nhật BDEF bằng diện tích hình thoi ABCD.

Từ đó suy ra cách tính diện tích hình thoi: Diện tích hình thoi bằng nửa tích hai đường chéo.

Bài 34 (trang 128 SGK Toán 8 Tập 1): Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật. Vì sao tứ giác này là một hình thoi? So sánh diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.

Giải:

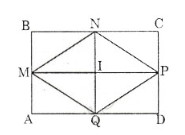
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh là M, N, P, Q.

Vẽ tứ giác MNPQ

Lại có: ABCD là hình chữ nhật nên AC = BD (3)

Từ (1), (2) và (3) suy ra: MN = PQ = MQ = NP

=> Tứ giác MNPQ là hình thoi.

+ Ta có:

∆ BMN = ∆ IMN; ∆ INP = ∆ CNP, ∆ AMQ= ∆IMQ, ∆ DPQ= ∆IPQ

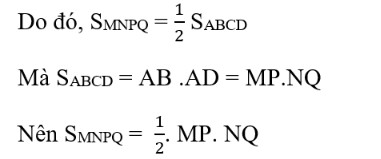
Như vậy diện tích hình thoi bằng nửa tích hai đường chéo.

Bài 35 (trang 129 SGK Toán 8 Tập 1): Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là 60o.

Giải:

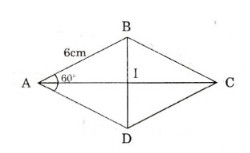
Cho hình thoi ABCD có cạnh AB = 6cm, góc ∠A = 60o.

- Cách 1:

ΔABD là tam giác đều nên BD = AB = 6cm

I là giao điểm của AC và BD => AI ⊥ DB

⇒ AI là đường cao của tam giác đều ABD nên

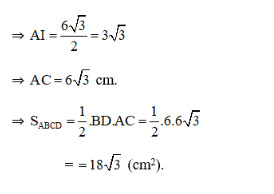
- Cách 2:

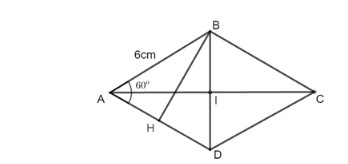
Khi đó ΔABD là tam giác đều. Từ B vẽ BH ⊥ AD thì HA = HD.

Nên tam giác vuông AHB là nửa tam giác đều.

BH là đường cao tam giác đều cạnh 6cm, nên

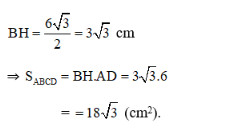
Bài 36 (trang 129 SGK Toán 8 Tập 1): Cho một hình thoi và một hình vuông có cùng chu vi. Hỏi hình nào có diện tích lớn hơn? Vì sao?

Giải:

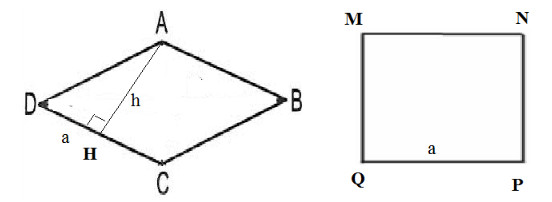
Giả sử hình thoi ABCD và hình vuông MNPQ có cùng chu vi là 4a

Suy ra cạnh hình thoi và cạnh hình vuông đều có độ dài a

Ta có: S_MNPQ = a

Từ đỉnh góc từ A của hình thoi ABCD, vẽ đường cao AH có độ dài là h.

ABCD là hình thoi

⇒ ABCD là hình bình hành

⇒ S_ABCD = ah

Mà ta luôn có h ≤ a (đường vuông góc nhỏ hơn đường xiên)

⇒ ah ≤ a² ⇒ S_ABCD ≤ S_MNPQ

Vậy diện tích hình vuông luôn lớn hơn diện tích hình thoi.

BÀI TẬP TÍNH DIỆN TÍCH HÌNH THOI LỚP 8 SBT

Bài 43 trang 163 SBT Toán 8 Tập 1: Tính diện tích hình thoi, biết cạnh của nó dài 6,2cm và một trong các góc của nó bằng 30°.

Giải:

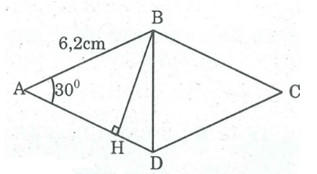
Giả sử hình thoi ABCD có AB = 6,2cm; ∠A = 30o

Từ B kẻ BH ⊥ AD (H ∈ AD)

Tam giác vuông AHB là một nửa tam giác đều cạnh AB nên:

BH = 1/2 AB = 3,1 (cm)

Vậy SABCD = BH.AD = 3,1.6,2 = 19,22 (cm2)

Bài 44 trang 163 SBT Toán 8 Tập 1: Cho hình thoi ABCD, biết AB = 5cm, AI = 3cm (I là giao điểm của hai đường chéo). Hãy tính diện tích hình thoi.

Giải:

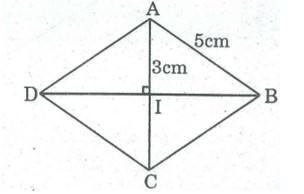
Áp dụng Pi-ta-go vào tam giác vuông IAB, ta có: AB² = AI² + IB²

⇒ IB2 = AB2 - AI2 = 25 - 9 = 16

⇒ IB = 4(cm).

AC = 2AI = 2.3 = 6 (cm)

BD = 2IB = 2.4 = 8 (cm)

SABCD = 1/2 AC.BD = 1/2 .6.8 = 24 (cm2)

Bài 45 trang 163 SBT Toán 8 Tập 1: a. Hãy vẽ một tứ giác có hai đường chéo vuông góc với nhau, biết độ dài hai đường chéo đó là a và 1/2.

a . Hỏi vẽ được bao nhiêu hình như vậy.

b. Có thể vẽ được mấy hình thoi, biết độ dài hai đường chéo là a và 1/2 a.

c. Hãy tính điện tích các hình vẽ đó

Giải:

a. Vẽ được vô số hình tứ giác thỏa mãn yêu cầu

b. Vẽ được duy nhât một hình thm có 2 đường chéo là a và 1/2 a

c. Diện tích các hình vẽ đó là: S = 1/2 a. 1/2 a = 1/4 a2 (đvdt).

Bài 46 trang 163 SBT Toán 8 Tập 1: Hai đường chéo hình thoi có độ dài là 16 cm và 12 cm. Tính:

a. Diện tích hình thoi

b. Độ dài cạnh hình thoi

Giải:

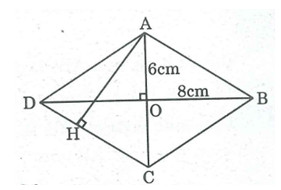
a. Ta có: SABCD = 1/2 AC.BD = 1/2 .12.16 = 96 (cm2)

b. ABCD là hình thoi có O là giao điểm của hai đường chéo nên:

AO = OC = 6cm; OB = OD = 8cm

Trong tam giác vuông OAB, ta có:

AB² = OA² + OB² = 6² + 8² = 100

AB = 10 (cm)

c. Kẻ AH ⊥ CD (H ∈ CD)

Ta có: SABCD = AH.CD ⇒ AH = SABCD / CD = 96/10 = 9,6 (cm)

Bài 5.2 trang 163 SBT Toán 8 Tập 1: Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Biết AC = 6cm, BD = 8cm. Gọi M, N, P, Q theo thứ tự là trung điểm các cạnh AB, BC, CD, DA. Gọi X, Y, Z, T theo thứ tự là trung điểm các cạnh MN, NP, PQ, QM.

a. Chứng minh rằng MNPQ là hình chữ nhật.

b. Tính diện tích của tứ giác XYZT.

Giải:

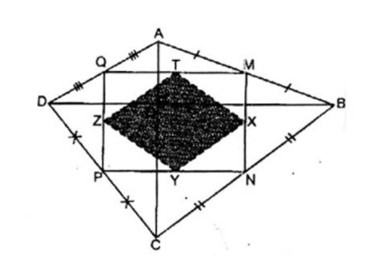
a. Trong ΔABD ta có:

M là trung điểm của AB

Q là trung điểm của AD nên MQ là đường trung bình của ΔABD.

⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)

Trong ΔCBD ta có:

N là trung điểm của BC

P là trung điểm của CD

nên NP là đường trung bình của ΔCBD

⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành

AC ⊥ BD (gt)

MQ // BD

Suy ra: AC ⊥ MQ

Trong ΔABC có MN là đường trung bình ⇒ MN // AC

Suy ra: MN ⊥ MQ hay (NMQ) = 90o

Vậy tứ giác MNPQ là hình chữ nhật.

b. Kẻ đường chéo MP và NQ

Trong ΔMNP ta có:

X là trung điểm của MN

Y là trung điểm của NP

nên XY là đường trung bình của ΔMNP

⇒ XY // MP và XY = 1/2 MP (tính chất đường trung bình của tam giác) (3)

Trong ΔQMP ta có:

T là trung điểm của QM

Z là trung điểm của QP

nên TZ là đường trung bình của ΔQMP

⇒ TZ // MP và TZ = 1/2 MP (tính chất đường trung bình của tam giác) (4)

Từ (3) và (4) suy ra: XY // TZ và XY = TZ nên tứ giác XYZT là hình bình hành.

Trong ΔMNQ ta có XT là đường trung bình

⇒ XT = 1/2 QN (tính chất đường trung bình của tam giác)

Tứ giác MNPQ là hình chữ nhật ⇒ MP = NQ

Suy ra: XT = XY. Vậy tứ giác XYZT là hình thoi

SXYZT = 1/2 XZ. TY

mà XZ = MQ = 1/2 BD = 1/2. 8 = 4 (cm);

TY = MN = 1/2 AC = 1/2 .6 =3 (cm)

Vậy: SXYZT = 1/2. 3. 4 = 6( cm2)

BÀI TẬP TÍNH DIỆN TÍCH HÌNH THOI LỚP 8 NÂNG CAO, BỔ SUNG

I. Bài Tập Trắc Nghiệm

Bài 1: Cho hình thoi có độ dài hai đường chéo lần lượt là 8cm, 10cm. Diện tích hình thoi là?

A. 80cm2. B. 40cm2. C. 18cm2. D. 9cm2.

Giải:

Diện tích của hình thoi là S = 1/2d1.d2

Trong đó d1,d2 lần lượt là độ dài hai đường chéo.

Khi đó, diện tích của hình thoi là Shình thoi = 1/2.8.10 = 40( cm2 )

Chọn đáp án B.

Bài 2: Hình thoi có độ dài hai đường chéo lần lượt là a√ 2 ,cm, a√ 3 cm. Diện tích của hình thoi là?

A. a2√ 6 cm2 B. (a2√ 6 )/3cm2 C. (a2√ 6 )/2cm2 D. (a2√ 5 )/2cm2

Giải:

Diện tích của hình thoi là S = 1/2d1.d2

Trong đó d1,d2 lần lượt là độ dài hai đường chéo.

Khi đó, diện tích của hình thoi là Shình thoi = 1/2. a√ 2 . a√ 3 = (a2√ 6 )/2cm2

Chọn đáp án C.

Bài 3: Cho hình thoi ABCD có AB = BC = CD = DA = 4cm và BACˆ = 600. Diện tích của hình thoi ABCD là?

A. 8cm2 B. 8√ 3 cm2 C. 16cm2 D. 16√ 3 cm2

Giải:

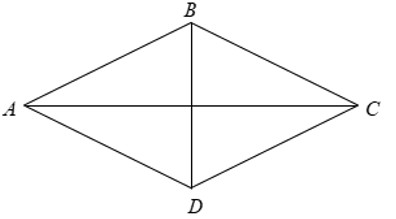
Xét hình thoi ABCD có BACˆ = 600.

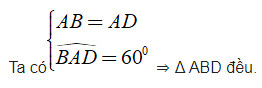
⇒ AB = AD = BD = 4cm

Gọi H là giao điểm của hai đường chéo AC,BD.

Áp dụng định lí Py - ta - go ta có:

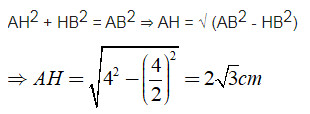
⇒ AC = 2AH = 4√ 3 ( cm )

Do đó SABCD = 1/2AC.BD = 1/2.4√ 3 .4 = 8√ 3 cm2

Chọn đáp án B.

Bài 4: Cho hình thoi ABCD có chu vi bằng 40cm và đường chéo BD = 8cm. Diện tích của hình thoi là?

A. 16cm2 B. 8√ 21 cm2 C. 16√ 21 cm2 D. 8cm2

Giải:

Gọi H là giao điểm của hai đường chéo AC,BD.

⇒ HB = HD = 4cm

Theo giải thiết ta có:

P_ABCD = AB + BC + CD + DA = 40

⇒ AB = BC = CD = DA = 10cm

Áp dụng định lý Py - ta - go ta có:

⇒ AC = 2AH = 4√ 21 cm

Do đó S_ABCD = 1/2.BD.AC = 1/2.4√ (21) .8 = 16√ 21 cm2

Chọn đáp án C.

II. Bài Tập Tự Luận

Bài 1: Cho hình thoi ABCD có AB = 13cm, AC = 10cm. Tính diện tích của hình thoi?

Giải:

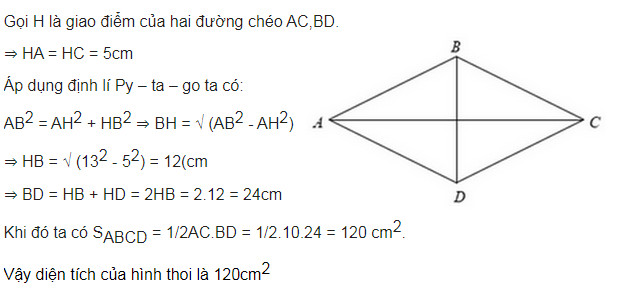
Bài 2: Tính diện tích hình thoi có cạnh là 17cm và tổng hai đường chéo là 46cm.

Giải:

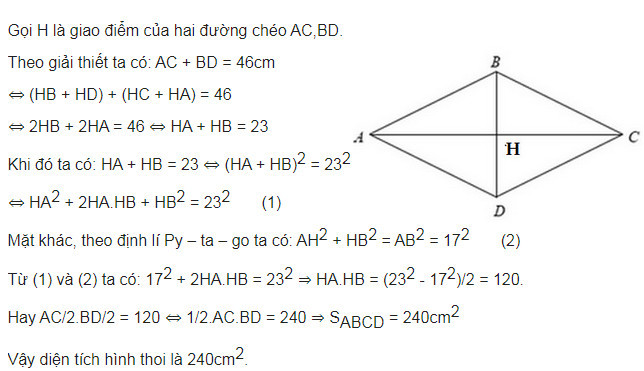
https://thuthuat.taimienphi.vn/bai-tap-tinh-dien-tich-hinh-thoi-lop-8-58479n.aspx
Các em nhớ để giấy nháp, sau khi đọc bài tập xong thì các em nên hình dung ra phương pháp giải bài toán trước khi bắt tay vào làm để hình thành được cách tư duy giải bài tập. Để sử dụng đầy đủ các dữ kiện của bài tập tính diện tích hình thoi lớp 8 và làm bài đơn giản hơn, các em nhớ viết giả thiết và kết luận của bài

Tác giả: Chipu