Trắc nghiệm bài 4 Định lí và chứng minh một định lí (P1)

Câu 1: Hãy phát biểu phần còn thiếu của kết luận trong định lí sau: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong ...

• song song;
• cắt nhau;
• bằng nhau;
• vuông góc;

Câu 2: Điền vào chỗ chấm phần kết luận để hoàn thành định lí sau:

Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong …

• Bằng nhau;
• Kề nhau;
• Phụ nhau;
• Kề bù nhau.

Câu 3: ChọnCâu sai. Điền vào chỗ trống bằng những nội dung thích hợp để được các định lí: “Nếu tia Ot là tia phân giác của góc xOy thì …”

• Ot nằm giữa hai tia Ox và Oy;
• $\widehat{xOt}=\widehat{tOy}$
• $\widehat{xOt}=\widehat{tOy}=\frac{\widehat{xOy}}{2}$
• $\widehat{xOt}=\widehat{tOy}=\widehat{xOy}$

Câu 4: Phát biểu bằng lời định lí sau:

GT	a // b; c ⊥ a.
KL	c ⊥ b .

• Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia
• B.Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia
• Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng một góc 60$^{\circ}$
• không có đáp án đúng

Câu 5: Chọn câu đúng.

• Giả thiết của định lý là điều cho biết;
• Kết luận của định lý là điều được suy ra;
• Giả thiết của định lý là điều được suy ra;
• Cả A, B đều đúng.

Câu 6: Điền vào chỗ chấm phần giả thiết để hoàn thành định lí sau:

Nếu hai đường thẳng phân biệt cùng … với một đường thẳng thứ ba thì chúng song song với nhau.

• Song song;
• Vuông góc;
• Cắt nhau;
• A, B, C đều đúng.

Câu 7: Trong các câu sau, câu nào cho một định lí

• Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
• Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia
• Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song
• Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song

Câu 8: Trong các câu sau, câu nào không cho một định lí

• Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
• Nếu một đường thẳng cắt hai đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau
• Hai góc đối đỉnh thì bằng nhau
• Hai góc kề nhau có tổng số đo là 180$^{\circ}$

Câu 9:  Phát biểu bằng lời định lí sau:

GT	$\widehat{A}+\widehat{B}=90^{\circ};\widehat{A}+\widehat{C}=90^{\circ}$
KL	$\widehat{B}=\widehat{C}$

• Hai góc cùng phụ một góc thứ ba thì bằng nhau;
• Hai góc cùng bù một góc thứ ba thì bằng nhau;
• Hai góc cùng phụ một góc thứ ba thì bù nhau;
• Hai góc cùng phụ một góc thứ ba thì kề nhau.

Câu 10: Hãy chỉ ra giải thiết của định lí sau: Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song.

• Một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau;
• Hai đường thẳng đó song song;
• Đáp án A và B đúng;
• Đáp án A và B sai.

Câu 11: Trong định lí “Hai góc đối đỉnh thì bằng nhau”. Giả thiết của định lí là:

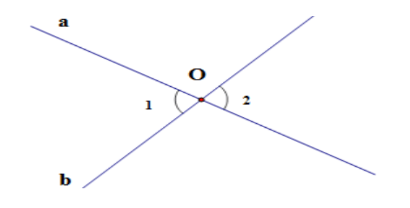
• a cắt b tại O;
• góc O1 và góc O2 là hai góc đối đỉnh;
• góc O1 và góc O2 là hai góc bằng nhau;
• góc O1 và góc O2 là hai góc nhọn.

Câu 12: Trong các câu sau,Câu nào cho một định lí:

• Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông;
• Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc nhọn;
• Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc bẹt;
• Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc tù.

Câu 13: Chọn câu sai:

• Định lí thường được phát biểu ở dạng: "Vì ... nên ..."
• Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
• Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra một phản ví dụ
• Để chỉ ra một khẳng định đúng, ta đi chứng minh

Câu 14: Cho định lí: "Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau. Giả thiết của định lí là:

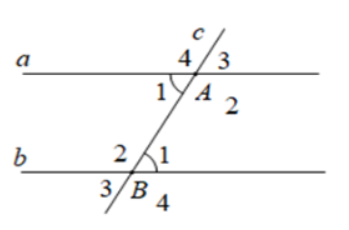
• $a//b; a\perp c$
• $a//b,c\cap a={A};c\cap b={B}$
• a//b; a//c
• a//b, c bất kì

Câu 15: Khi chứng minh một định lí, người ta cần:

• Chứng minh định lí đó đúng trong một trường hợp cụ thể của giả thiết;
• Chứng minh định lí đó đúng trong hai trường hợp cụ thể của giả thiết;
• Chứng minh định lí đó đúng trong mọi trường có thể xảy ra của giả thiết;
• Chứng minh định lí đó đúng trong vài trường hợp cụ thể của giả thiết.

Câu 16: Phát biểu bằng lời định lí sau:

GT	a ⊥ c; b ⊥ c.
KL	a // b .

• Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau;
• B.Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau;
• Nếu hai đường thằng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau;
• Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.

Câu 17: Điền vào chỗ trống bằng những nội dung thích hợp để được các định lí: “Nếu M là trung điểm của đoạn thẳng AB thì …”

• M nằm giữa A và B;
• MA = MB;
• MA = MB = AB;
• MA + MB = AB.

Câu 18: Chọn khẳng định đúng trong những khẳng định sau đây.

• Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận;
• Định lí là một khẳng định được suy ra từ những khẳng định được coi là đúng;
• A, B đều đúng;
• A, B đều sai.

Câu 19: Trong định lí “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”.

Giả thiết: a // b, a ⊥ c. Kết luận của định lí trên là:

• a // b, a ⊥c;
• a // b;
• b ⊥c;
• a // b, a ⊥c, b ⊥ c.

Câu 20: Cho định lí có giả thiết: góc xOy và x’Oy’ là hai góc đối đỉnh (như hình vẽ). Kết luận của định lí là:

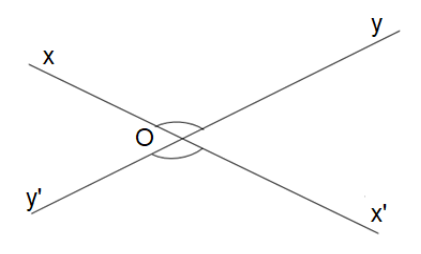
• $\widehat{xOy}=\widehat{x'Oy'}$
• B. $\widehat{xOy}=\widehat{x'Oy}$
•  $\widehat{xOy}=\widehat{xOy'}$
• A, B đều đúng.

Hãy trả lời các câu hỏi để biết kết quả của bạn